Löse die folgenden Problemstellungen:
Es sollen 8 Stapel Bücher so angeordnet werden, dass auf den ersten Stapel 2 Bücher kommen und auf jeden weiteren Stapel jeweils zwei Bücher mehr als auf den vorherigen. Wie viele Bücher sollen insgesamt angeordnet werden?
Dieses Feld ist erforderlich.
Die Stapel Bücher, die gestapelt werden sollen, entsprechen den ersten 8 Gliedern der arithmetischen Folge 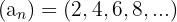 , deren Differenz
, deren Differenz  ist.
ist.
Somit ist 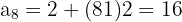
Die Anzahl der Bücher, die platziert werden sollen, ist also die Summe der ersten acht Glieder dieser Folge:
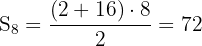
Es müssen also 72 Bücher platziert werden.
Die größere Kathete eines rechtwinkligen Dreiecks misst 16 cm. Berechne die Länge der beiden anderen Seiten, wenn du weißt, dass die drei Seiten des Dreiecks in arithmetischer Folge stehen.
Hypotenuse
Kleinere Kathete
Dieses Feld ist erforderlich.
Wir ordnen die gegebenen Informationen:
Kleinere Kathete 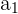
Größere Kathete 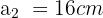
Hypotenuse 
Differenz 
Da es sich um eine arithmetische Folge handelt, gilt:
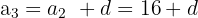
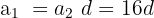
Andererseits ergibt sich unter Anwendung des Satzes des Pythagoras:
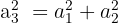
Wir setzen die Werte von a1, a2 und a3 in den obigen Ausdruck ein und erhalten:
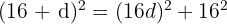
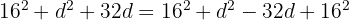
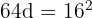
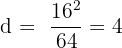
Daher beträgt die Differenz der arithmetischen Folge, der die Seiten dieses Dreiecks folgen, 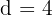 .
.
Somit haben wir:
Hypotenuse 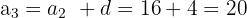
Kleinere Kathete 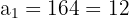
Wandle die periodische Dezimalzahl unter Verwendung der Summe einer arithmetischen Folge in einen Bruch um:
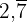 = /
= /
Dieses Feld ist erforderlich.
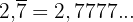
Diese Zahl können wir wie folgt schreiben:
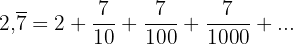
Wir stellen fest, dass die Zahl die Summe aus 2 plus der Summe der Glieder der geometrischen Folge ist, die wie folgt gegeben ist:
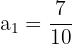 und
und 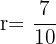
Wir schreiben also:
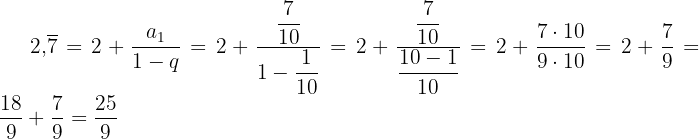
Schreibe die gemischt periodische Dezimalzahl unter Verwendung der Summe einer arithmetischen Folge als Bruch:
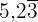 =/
=/
Dieses Feld ist erforderlich.
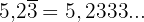
Diese Zahl können wir wie folgt schreiben:
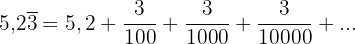
Wir stellen fest, dass die Zahl die Summe aus 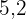 plus der Summe der Glieder der geometrischen Folge ist, die wie folgt gegeben ist:
plus der Summe der Glieder der geometrischen Folge ist, die wie folgt gegeben ist:
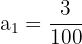 und
und 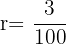
Wir schreiben also:
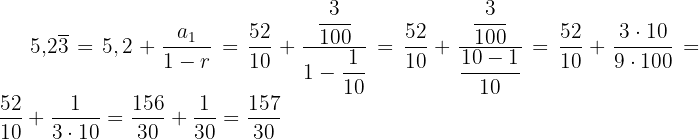
Gegeben ist ein Quadrat mit einer Seitenlänge von 2 cm. Wir konstruieren ein weiteres Quadrat innerhalb dieses Quadrats auf den Mittelpunkten seiner Seiten und nach dem gleichen Verfahren ein weiteres Quadrat innerhalb dieses Quadrats und so weiter. Berechne die Summe der Flächen der auf diese Weise konstruierten unendlichen Quadrate.
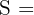
Dieses Feld ist erforderlich.
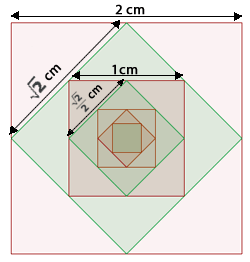
Wir nennen  die Fläche des Ausgangsquadrats,
die Fläche des Ausgangsquadrats, 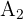 die Fläche des zweiten Quadrats, das entsteht,
die Fläche des zweiten Quadrats, das entsteht, 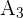 das darauffolgende Quadrat und so weiter.
das darauffolgende Quadrat und so weiter. 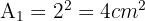
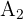
Um die Fläche von 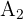 zu ermitteln, müssen wir die Länge seiner Seiten berechnen. Dazu genügt es, das in der Abbildung dargestellte rechtwinklige Dreieck zu betrachten und die Länge seiner Hypotenuse zu ermitteln..
zu ermitteln, müssen wir die Länge seiner Seiten berechnen. Dazu genügt es, das in der Abbildung dargestellte rechtwinklige Dreieck zu betrachten und die Länge seiner Hypotenuse zu ermitteln.. 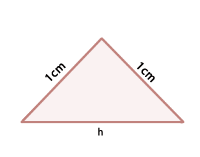
Jede Kathete misst 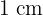 , da sie die Hälfte der Seite des ursprünglichen Quadrats ist.
, da sie die Hälfte der Seite des ursprünglichen Quadrats ist.
Wir haben also: 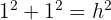
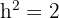
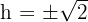
Da  eine Größe ist, nehmen wir nur die positive Lösung, sodass
eine Größe ist, nehmen wir nur die positive Lösung, sodass
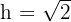
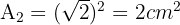
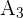
Um die Fläche von 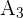 zu berechnen, müssen wir die Länge seiner Seite berechnen. Dazu genügt es, das in der Abbildung markierte rechtwinklige Dreieck zu betrachten und die Länge seiner Hypotenuse zu ermitteln.
zu berechnen, müssen wir die Länge seiner Seite berechnen. Dazu genügt es, das in der Abbildung markierte rechtwinklige Dreieck zu betrachten und die Länge seiner Hypotenuse zu ermitteln. 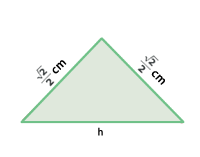
Jede Kathete misst 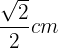 , da sie die Hälfte der Seite des vorherigen Quadrats ist.
, da sie die Hälfte der Seite des vorherigen Quadrats ist.
Somit haben wir:
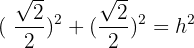
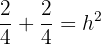
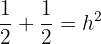
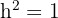
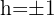
Da  eine Größe ist, nehmen wir nur die positive Lösung, sodass
eine Größe ist, nehmen wir nur die positive Lösung, sodass
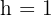
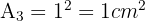
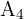
Um die Fläche von 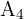 zu berechnen, müssen wir die Länge seiner Seite berechnen. Dazu genügt es, das in der Abbildung markierte rechtwinklige Dreieck zu betrachten und die Länge seiner Hypotenuse zu ermitteln.
zu berechnen, müssen wir die Länge seiner Seite berechnen. Dazu genügt es, das in der Abbildung markierte rechtwinklige Dreieck zu betrachten und die Länge seiner Hypotenuse zu ermitteln. 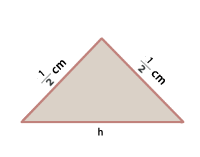
Jede Kathete misst 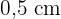 , da sie die Hälfte der Seite des vorherigen Quadrats ist.
, da sie die Hälfte der Seite des vorherigen Quadrats ist.
Wir haben also:
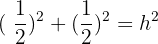
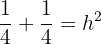
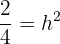
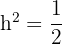
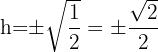
Da  eine Größe ist, nehmen wir nur die positive Lösung, sodass
eine Größe ist, nehmen wir nur die positive Lösung, sodass
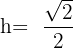
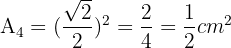
Die Flächen der Quadrate bilden eine geometrische Folge:
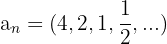 im Verhältnis
im Verhältnis 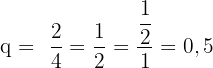
Somit ist die unendliche Summe: 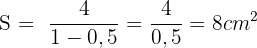
Berechne die Summe aller geraden dreistelligen Zahlen.
Dieses Feld ist erforderlich.
Wir stellen fest, dass die geraden dreistelligen Zahlen zu einer arithmetischen Folge 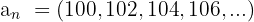 gehörten, deren Differenz
gehörten, deren Differenz  ist
ist
Außerdem entspricht die Anzahl der geraden dreistelligen Zahlen der Anzahl der geraden Zahlen zwischen 100 und 998. Wir berechnen diese Anzahl:
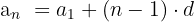
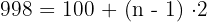
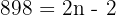
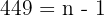
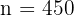
Unser Problem beschränkt sich also darauf, die Summe der ersten 450 Glieder der arithmetischen Folge 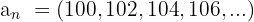 zu berechnen.
zu berechnen.
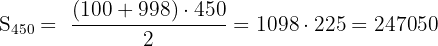
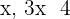 und
und 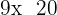 sind drei Zahlen einer geometrischen Folge. Berechne den Wert von
sind drei Zahlen einer geometrischen Folge. Berechne den Wert von  .
.
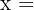
Wie lautet das Verhältnis dieser Folge?

Dieses Feld ist erforderlich.
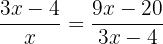
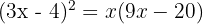
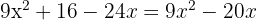
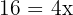
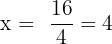
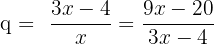
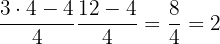
Ein General, der für einen Trupp von 820 Soldaten verantwortlich ist, möchte diese in Dreiecksformation aufstellen, sodass die erste Reihe aus einem Soldaten, die zweite aus zwei Soldaten, die dritte aus drei Soldaten usw. besteht. Wie viele Reihen werden gebildet?
Dieses Feld ist erforderlich.

Wir stellen fest, dass die Anordnung der Soldaten in Reihen eine arithmetische Folge 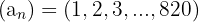 der Differenz
der Differenz  bildet, deren erstes Glied
bildet, deren erstes Glied 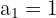 und deren Summe
und deren Summe 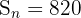 ist
ist
Wir müssen nun den Wert von  ermitteln.
ermitteln.
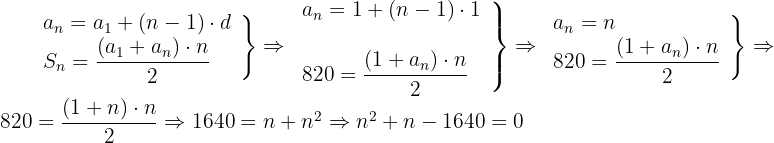
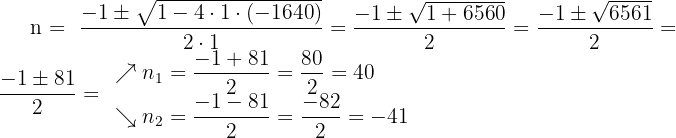
Die negative Lösung ist ungültig, da wir uns auf die Anzahl der Reihen beziehen, die die Soldaten bilden.
Es werden also 40 Reihen gebildet.
Die Seiten eines Fünfecks mit einem Umfang von 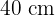 bilden eine arithmetische Folge. Die größere Seite misst
bilden eine arithmetische Folge. Die größere Seite misst  . Wie lang ist die kleinste Seite?
. Wie lang ist die kleinste Seite?

Dieses Feld ist erforderlich.
Da die Seitenlängen in arithmetischer Folge angeordnet sind, gibt es eine Differenz  , sodass die Seitenlängen von der größten zur kleinsten wie folgt angeordnet sind:
, sodass die Seitenlängen von der größten zur kleinsten wie folgt angeordnet sind:

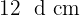
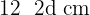
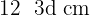
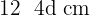
Da der Umfang 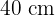 beträgt, gilt:
beträgt, gilt:
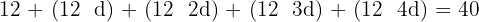
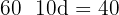
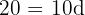

Die Länge der kürzeren Seite beträgt also 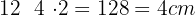
Die Glocke der Dorfkirche von Josef schlägt zu jeder vollen Stunde so oft, wie die Uhrzeit angibt. Außerdem schlägt sie jede halbe Stunde einmal. Gib die Anzahl der Glockenschläge an, die sie im Laufe eines Tages schlägt.
Glockenschläge
Dieses Feld ist erforderlich.
Da jede halbe Stunde ein Glockenschlag ertönt und ein Tag 24 Stunden hat, ergeben diese Glockenschläge insgesamt 24, wobei zu berücksichtigen ist, dass der Glockenschlag um „halb eins” bereits einem neuen Tag entspricht.
Die Glockenschläge, die zu jeder vollen Stunde erklingen, folgen einer arithmetischen Folge, deren erstes Glied 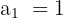 und
und  ist. Um die Gesamtzahl der Glockenschläge zu ermitteln, müssen wir also die Summe der ersten 12 Glieder dieser arithmetischen Folge und anschließend die Summe der ersten 11 Glieder berechnen.
ist. Um die Gesamtzahl der Glockenschläge zu ermitteln, müssen wir also die Summe der ersten 12 Glieder dieser arithmetischen Folge und anschließend die Summe der ersten 11 Glieder berechnen.
Hinweis: Auch wenn man zunächst denken könnte, dass man die Summe der ersten 24 Glieder berechnen muss, ist zu beachten, dass es sich um analoge Uhrzeiten handelt, sodass nach 12 Uhr mittags nicht 13 Glockenschläge, sondern nur 1 Glockenschlag für 13:00 Uhr ertönt, nicht 14 Glockenschläge, sondern nur 2 Glockenschläge für 14:00 Uhr und so weiter. Außerdem berücksichtigen wir in der zweiten Runde nicht die ersten 12 Glieder, sondern nur die ersten 11, da das zwölfte bereits Mitternacht entspricht, das als Teil des folgenden Tages betrachtet wird.
Wir berechnen also:
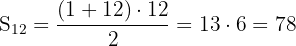
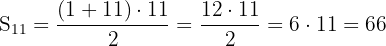
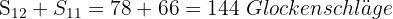
Die Gesamtzahl der Glockenschläge an einem Tag beträgt also: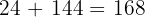
Mit KI zusammenfassen:


