Löse die folgenden Probleme:
In einem Park meiner Stadt wurde das folgende Denkmal in Form einer Kugel errichtet. Gib das Volumen und die Oberfläche dieser Kugel mit einem Durchmesser von 70 dm an, auf zwei Dezimalstellen gerundet..

A = dm²
V = dm³
Dieses Feld ist erforderlich.
Da die Kugel einen Durchmesser von 70 dm hat, ist ihr Radius 35 dm
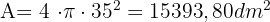
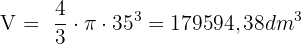
Gib den Radius einer Seifenblase mit einem Volumen von 12π cm³ an.
r = cm
Dieses Feld ist erforderlich.
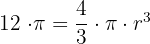
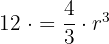
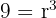
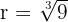
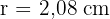
Berechne den Flächeninhalt der folgenden Figur.
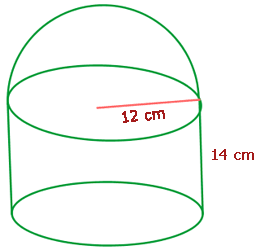
A = cm²
Dieses Feld ist erforderlich.
Die Fläche des Zylinders ist die Summe aus der Seitenfläche und der Grundfläche.:
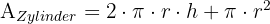
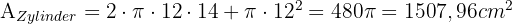
Die Fläche der Halbkugel ist:
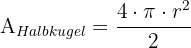
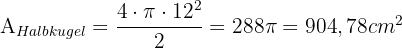
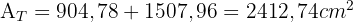
Vereinfacht gesagt kann man sagen, dass eine Orange eine Kugel ist. Alex isst 7 der 12 Segmente einer Orange mit einem Durchmesser von 10 cm. Wie groß war das Volumen der von Alex gegessenen Orange? Runde auf zwei Dezimalstellen.
V = cm³
Dieses Feld ist erforderlich.
Das Problem besteht darin, das Volumen eines kugelförmigen Stücks zu berechnen, wobei der Radius der Orange 5 cm und n = 360 : 12 = 30º ist.
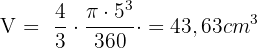
Da er 5 Stücke gegessen hat, beträgt das gegessene Volumen:
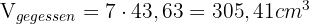
Berechne die Höhe der folgenden Figur so, dass ihre Fläche mit der einer sphärischen Spindel mit einer Breite von 20º übereinstimmt. Un wenn ihr Durchmesser 12 cm ist? Hängt der dann vom Radius der Kugel ab? Ja oder nein?
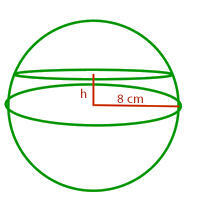
h = cm
h = cm
Dieses Feld ist erforderlich.
Wir stellen fest, dass es sich um eine Kugelschicht handelt. Wir berechnen die Fläche der kugelförmigen Spindel und setzen sie mit der Fläche der Kugelschicht gleich, um die Höhe zu berechnen..
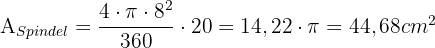
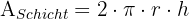
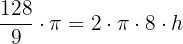
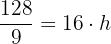
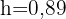
Wenn der Radius nun 12 : 2 = 6 cm misst:
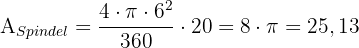
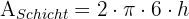

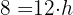
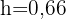
Wir erhalten für die Höhe unterschiedliche Werte. Dies zeigt, dass der Radius bei der Berechnung tatsächlich eine Rolle spielt. Wir hätten die Höhe auch wie folgt berechnen können:
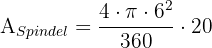
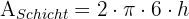
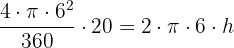
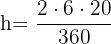
und allgemein: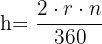
Berechne die Fläche und das Volumen eines Kugelsegments mit einer Höhe von 6 cm und einem Radius von 9 cm. Runde auf zwei Dezimalstellen..
A = cm²
V = cm³
Dieses Feld ist erforderlich.
Um die Fläche des Segments zu berechnen, muss der Radius der Kugel, zu der es gehört, bekannt sein:
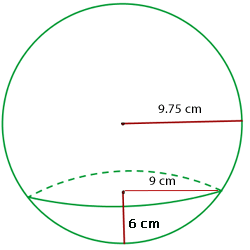
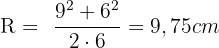
Die Fläche und das Volumen sind dann:
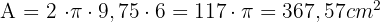
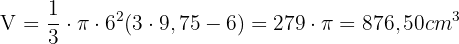
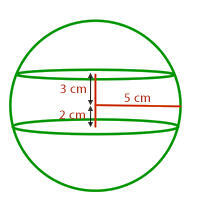
Berechne die Fläche und das Volumen der Kugelschicht, die entsteht, wenn eine Kugel mit einem Durchmesser von 10 cm durch zwei parallele Ebenen geschnitten wird, die jeweils 2 cm und 3 cm vom Mittelpunkt der Kugel entfernt sind.
A = cm²
Angenommen, wir kaufen eine weitere Kugel wie die vorherige, berechne das Volumen der Kugelschicht, deren Umfänge einen Radius von 5 cm und 4 cm haben und deren Abstand zwischen ihnen 2,5 cm beträgt.
V = cm³
Dieses Feld ist erforderlich.
Wir lösen den ersten Teil des Problems. Da wir den Radius der beiden Kreise, die durch den Schnitt mit der Ebene entstehen, nicht kennen, müssen wir die Fläche anhand des Radius der Kugel und der angegebenen Höhen berechnen. Das heißt, wir müssen die Fläche der beiden Kugelsegmente berechnen und diese dann von der Fläche der gesamten Kugel abziehen:
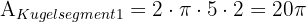
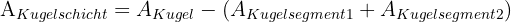
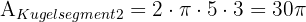
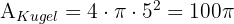
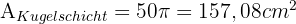
Den zweiten Teil des Problems können wir direkt lösen. Wir setzen einfach in die Formel für die Berechnung eines Kugelsegments ein.
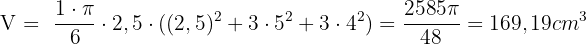
Mit KI zusammenfassen:


