Gegeben ist ein Zauberwürfel, dessen Seitenfläche aus  Quadraten besteht. Jedes dieser Quadrate hat eine Seitenlänge von
Quadraten besteht. Jedes dieser Quadrate hat eine Seitenlänge von 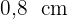 . Berechne seinen Flächeninhalt und sein Volumen.
. Berechne seinen Flächeninhalt und sein Volumen.
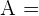

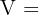

Dieses Feld ist erforderlich.
1Um die Fläche und das Volumen zu berechnen, müssen wir den Wert der Kante kennen.
Jede Seite des Würfels enthält  Quadrate, sodass jede Kante aus drei Seiten der Quadrate mit einer Seitenlänge von
Quadrate, sodass jede Kante aus drei Seiten der Quadrate mit einer Seitenlänge von 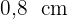 besteht
besteht
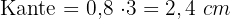
2Um die Gesamtfläche zu berechnen, berechnen wir die Fläche jeder Seite und multiplizieren sie mit 
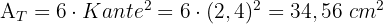
3Wir berechnen das Volumen
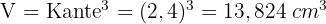
Gegeben ist ein Würfel mit einer Diagonale von 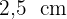 . Gib die Fläche und das Volumen des Würfels mit zwei Dezimalstellen an.
. Gib die Fläche und das Volumen des Würfels mit zwei Dezimalstellen an.
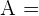

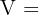

Dieses Feld ist erforderlich.
1Um die Fläche und das Volumen zu berechnen, müssen wir den Wert der Kante kennen
Die Diagonale  des Würfels hat diametral gegenüberliegende Eckpunkte des Würfels als Endpunkte und ist die Hypotenuse des rechtwinkligen Dreiecks, dessen Katheten die Diagonale
des Würfels hat diametral gegenüberliegende Eckpunkte des Würfels als Endpunkte und ist die Hypotenuse des rechtwinkligen Dreiecks, dessen Katheten die Diagonale  einer der Würfelseiten und eine Kante
einer der Würfelseiten und eine Kante  desselben sind
desselben sind
Wir berechnen die Diagonale einer der Seiten
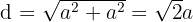
Wenn wir die Diagonale  kennen, erhalten wir die Länge der Kante
kennen, erhalten wir die Länge der Kante

2Um die Gesamtfläche zu berechnen, berechnen wir die Fläche jeder Seite und multiplizieren sie mit  .
.
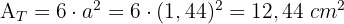
3Wir berechnen das Volumen
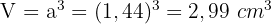
Angenommen, es gibt einen würfelförmigen Wassertank mit einem Fassungsvermögen von 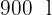 , gib die Fläche und das Volumen des Tanks mit zwei Dezimalstellen an.
, gib die Fläche und das Volumen des Tanks mit zwei Dezimalstellen an.
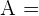

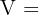
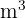
Dieses Feld ist erforderlich.
1Da ein Liter einem Kubikdezimeter entspricht, berechnen wir zunächst das Volumen
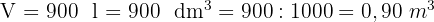
2Um die Kantenlänge zu berechnen, wenden wir die Formel für das Volumen an
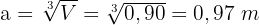
3Wir berechnen die Gesamtfläche
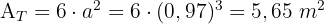
Berechne die Fläche und das Volumen der folgenden Figur:

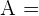

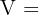

Dieses Feld ist erforderlich.
1Um die Fläche zu berechnen, stellen wir fest, dass es  Kreuze und
Kreuze und  Vertiefungen gibt. In jeder Vertiefung befinden sich
Vertiefungen gibt. In jeder Vertiefung befinden sich  Würfelseiten mit einer Kantenlänge von
Würfelseiten mit einer Kantenlänge von 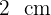 , sodass die Gesamtfläche der Figur der Gesamtfläche des Würfels mit einer Kantenlänge von
, sodass die Gesamtfläche der Figur der Gesamtfläche des Würfels mit einer Kantenlänge von  entspricht
entspricht
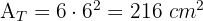
2Wir berechnen das Volumen
Das Volumen der Figur entspricht dem Volumen des gesamten Würfels, dessen Kantenlänge 3 · 2 = 6 cm beträgt, abzüglich des Volumens der Vertiefungen.
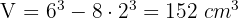
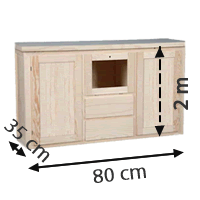
Ein Möbelstück wie das in der Abbildung hat die Form eines Quaders 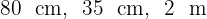 . Berechne sein Volumen und seine Fläche
. Berechne sein Volumen und seine Fläche
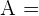

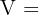

Dieses Feld ist erforderlich.
1Wir rechnen in gleiche Einheiten um
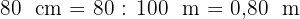
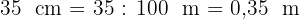
2Wir berechnen die Gesamtfläche

3Wir berechnen das Volumen
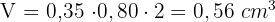
Gegeben ist ein Quader mit den Seitenlängen 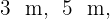 und einem Volumen von
und einem Volumen von  . Berechne die fehlende Seite und seinen Flächeninhalt
. Berechne die fehlende Seite und seinen Flächeninhalt
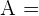

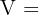

Dieses Feld ist erforderlich.
1Wir berechnen die fehlende Seite, indem wir die Formel für das Volumen anwenden

2Wir berechnen die Gesamtfläche
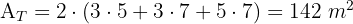
Wir wissen, dass ein Raum in einem gewöhnlichen Haus die Form eines Quaders hat. Wenn die Maße des Raums 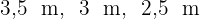 sind, würde ein 5 m langer Stahlträger in diesen Raum passen? Antworte: Ja oder Nein.
sind, würde ein 5 m langer Stahlträger in diesen Raum passen? Antworte: Ja oder Nein.
Bitte wähle eine Antwort aus.
1Wenn wir versuchen, den Balken der Länge oder Breite nach in den Raum einzubauen, passt er offensichtlich nicht hinein, da er größer ist als die gegebenen Maße. Wir können jedoch sehen, ob er diagonal hineinpasst, indem wir die Diagonale des Raumes berechnen.
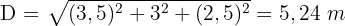
Da die Diagonale 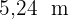 misst, ist es möglich, den Balken in den Raum einzubauen.
misst, ist es möglich, den Balken in den Raum einzubauen.
Ein Container in Quaderform hat die Maße 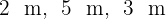 . Der Hersteller möchte die Wände des Containers mit Stahlstangen verstärken, die diagonal an jeder Wand angebracht werden, sodass jede Wand zwei Verstärkungen hat. Wie viele Stahlstangen werden dafür benötigt?
. Der Hersteller möchte die Wände des Containers mit Stahlstangen verstärken, die diagonal an jeder Wand angebracht werden, sodass jede Wand zwei Verstärkungen hat. Wie viele Stahlstangen werden dafür benötigt?

Dieses Feld ist erforderlich.
1 Wir berechnen die Diagonale der Seite 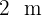 und
und 
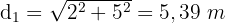
Es gibt zwei gleiche Wände, daher sind 4 diagonale Verstärkungen erforderlich, d. h. 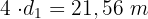
2 Wir berechnen die Diagonale der Seite 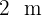 y
y 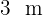
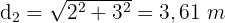
Es gibt zwei gleiche Wände, daher sind 4 diagonale Verstärkungen erforderlich, d. h. 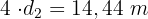
3 Wir berechnen die Diagonale der Seite 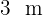 und
und 
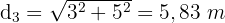
Es gibt zwei gleiche Wände, daher sind 4 diagonale Verstärkungen erforderlich, d. h. 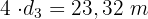
4 Die Anzahl der zu verwendenden Stahlstangen beträgt
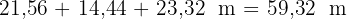
9 Die Maße einer Milchpackung sind 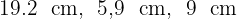 . Der Hersteller möchte die Verpackung ändern, indem er die Grundfläche um
. Der Hersteller möchte die Verpackung ändern, indem er die Grundfläche um  verringert und die Höhe um
verringert und die Höhe um  erhöht.
erhöht.
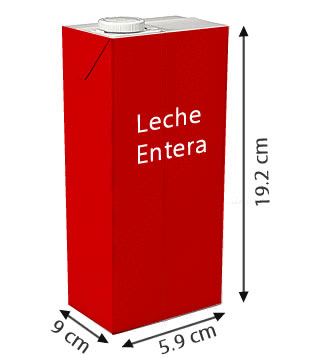
Berechne das Volumen der neuen Packung und runde auf zwei Dezimalstellen.
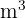
Dieses Feld ist erforderlich.
Um das Volumen der neuen Packung zu berechnen, berechnen wir die Grundfläche und die neue Höhe, da das Volumen des Quaders der Grundfläche mal der Höhe entspricht. Wir multiplizieren die Fläche der neuen Grundfläche mit 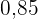 , da wir eine Verkleinerung um
, da wir eine Verkleinerung um  vorgenommen haben, und die Höhe mit
vorgenommen haben, und die Höhe mit 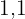 , da sie um
, da sie um  zunimmt
zunimmt

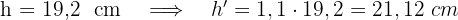
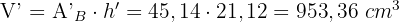
Wird die neue Verpackung weniger Milch enthalten?
Bitte wähle eine Antwort aus.
Um zu berechnen, ob die Packung weniger Milch enthält, berechnen wir ihr Volumen, bevor wir Änderungen daran vornehmen
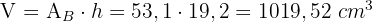
Das Volumen der neuen Packung ist geringer als das der alten, sodass die neue Packung weniger Milch enthält.
Wenn der Preis für die Verpackung 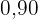 € beträgt und
€ beträgt und 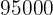 Liter Milch pro Monat verkauft werden, wie viel verdient das Unternehmen dann mit der neuen Verpackung?
Liter Milch pro Monat verkauft werden, wie viel verdient das Unternehmen dann mit der neuen Verpackung?
Dieses Feld ist erforderlich.
Wir rechnen Kubikzentimeter in Kubikdezimeter um und runden auf zwei Dezimalstellen
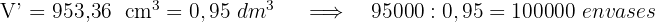
Wir berechnen den Gewinn
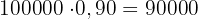 €
€
Mit KI zusammenfassen:


