Löse die folgenden Probleme:
1 Für einige Rollenspiele werden Würfel mit anderen als den üblichen Formen verwendet, beispielsweise diese tetraedrischen Würfel mit einer Kantenlänge von 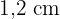 .
.
Gib das Volumen jedes dieser Würfel an und runde das Ergebnis auf zwei Dezimalstellen.
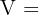

Dieses Feld ist erforderlich.
Um das Volumen des Tetraeders zu berechnen, verwenden wir die Formel 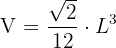 , wobei
, wobei  der gegebenen Kante annimmt.
der gegebenen Kante annimmt.
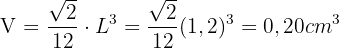
Um die Fläche jeder Seite zu berechnen, gibt es zwei Möglichkeiten.
Wie groß ist die Fläche jeder Seite dieses Würfels?
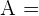

Dieses Feld ist erforderlich.
Um die Fläche jeder Seite zu berechnen, gibt es zwei Möglichkeiten.
1 Da alle Seiten gleich sind, reicht es aus, die Gesamtfläche zu berechnen und durch 4 zu teilen. 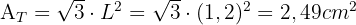
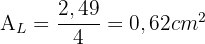
2 Es handelt sich um gleichseitige Dreiecke mit einer Seitenlänge von 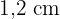

Um den Wert der Höhe zu ermitteln, wenden wir den Satz des Pythagoras an. 
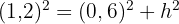
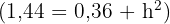
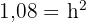

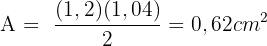
2 Berechne die Fläche und das Volumen eines Tetraeders mit einer Kantenlänge von 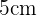 und runde gegebenenfalls auf zwei Dezimalstellen.
und runde gegebenenfalls auf zwei Dezimalstellen.
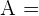

Dieses Feld ist erforderlich.
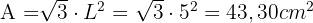
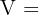

Dieses Feld ist erforderlich.
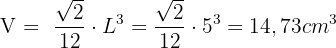
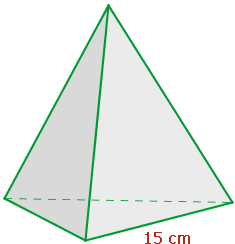
3 Berechne die Höhe, Fläche und das Volumen des folgenden Tetraeders, wobei das Apothema der Basis 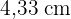 misst, und runde gegebenenfalls wieder auf zwei Dezimalstellen.
misst, und runde gegebenenfalls wieder auf zwei Dezimalstellen.
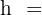

Dieses Feld ist erforderlich.
Zunächst berechnen wir das Apothema des Tetraeders, das uns später dabei helfen wird, dessen Höhe zu ermitteln. Um das Apothema zu ermitteln, betrachten wir eine Fläche des Tetraeders, die ein gleichseitiges Dreieck mit einer Seitenlänge von 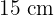 ist. Das Apothema des Tetraeders entspricht der Höhe eines dieser Dreiecke, die wir mithilfe des Satzes des Pythagoras berechnen:
ist. Das Apothema des Tetraeders entspricht der Höhe eines dieser Dreiecke, die wir mithilfe des Satzes des Pythagoras berechnen:


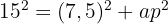
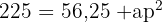
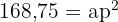
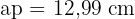
Um die Höhe des Tetraeders zu ermitteln, betrachten wir das folgende Dreieck und wenden erneut den Satz des Pythagoras an:
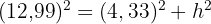
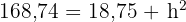
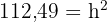
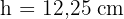
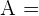

Dieses Feld ist erforderlich.
Anschließend berechnen wir die Fläche und das Volumen des Tetraeders: 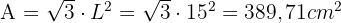
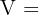

Dieses Feld ist erforderlich.
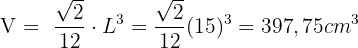
4 Martha hat eine Mineraliensammlung. Eines ihrer Lieblingsstücke ist ein Fluorit (in Form eines Oktaeders), das wir in der folgenden Zeichnung sehen können: Da wir wissen, dass seine Kante 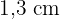 misst, können wir die Fläche und das Volumen dieses Sammlerstücks berechnen.
misst, können wir die Fläche und das Volumen dieses Sammlerstücks berechnen.

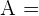

Dieses Feld ist erforderlich.
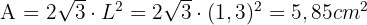
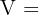

Dieses Feld ist erforderlich.
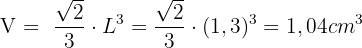
Wie groß ist der Flächeninhalt einer Seite? 
Dieses Feld ist erforderlich.
Um die Fläche einer Seite des Oktaeders zu berechnen, müssen wir berücksichtigen, dass es sich um ein regelmäßiges Polyeder handelt, das aus  gleichen gleichseitigen Dreiecken besteht.
gleichen gleichseitigen Dreiecken besteht.
Daher dividieren wir die Fläche des Oktaeders durch  und erhalten die Fläche einer seiner Seitenflächen.
und erhalten die Fläche einer seiner Seitenflächen.
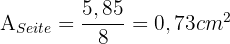
5 Berechne die Kantenlänge eines Oktaeders, dessen Fläche 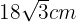 beträgt.
beträgt.

Dieses Feld ist erforderlich.
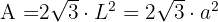
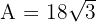
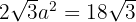
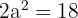
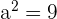
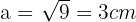
Wie groß wäre das Volumen? Runde auf zwei Dezimalstellen.

Dieses Feld ist erforderlich.
Anhand der Kantenlänge lässt sich das Volumen des Oktaeders ganz einfach berechnen:
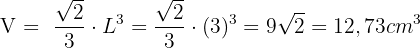
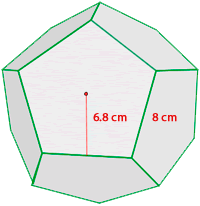
6 Berechne die Fläche und das Volumen eines Dodekaeders mit einer Kantenlänge von 8 cm, wenn das Apothema einer seiner Flächen 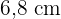 misst. Runde gegebenenfalls auf zwei Dezimalstellen.
misst. Runde gegebenenfalls auf zwei Dezimalstellen.
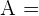

Dieses Feld ist erforderlich.
Es genügt, die uns bekannten Formeln für Fläche und Volumen des Dodekaeders anzuwenden.
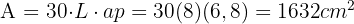
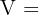

Dieses Feld ist erforderlich.
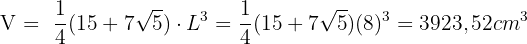
7 Berechne die Fläche und das Volumen des folgenden Kalenders, dessen Kantenlänge 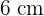 und dessen Apothema
und dessen Apothema 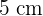 beträgt. Runde gegebenenfalls auf zwei Dezimalstellen.
beträgt. Runde gegebenenfalls auf zwei Dezimalstellen.

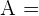

Dieses Feld ist erforderlich.
Wenn wir uns die Abbildung ansehen, erkennen wir, dass es sich um ein Dodekaeder handelt, sodass wir einfach die bekannten Formeln für Fläche und Volumen anwenden können.
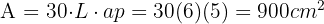
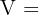

Dieses Feld ist erforderlich.
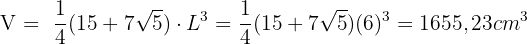
8Der Mathematiklehrer der Schüler der 9. Klasse gibt ihnen die folgende Abbildung eines Ikosaeders, dessen Kantenlänge 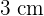 beträgt.
beträgt.
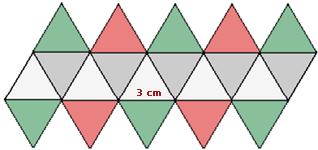
Wie lautet der Flächeninhalt der gebildeten Figur? 
Dieses Feld ist erforderlich.
Wir berechnen die Fläche und das Volumen unter Anwendung der für diese Figur bekannten Formeln.
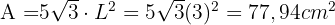
Und das Volumen? 
Dieses Feld ist erforderlich.
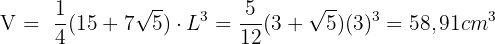
9 Die Gesamtfläche des Ikosaeders beträgt 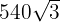 .
.
Wie lautet die Kantenlänge? Runde auf zwei Dezimalstellen.

Dieses Feld ist erforderlich.
Ausgehend von der Fläche berechnen wir die Kante, indem wir die Fläche mit der Formel, die wir zu ihrer Berechnung haben, gleichsetzen.

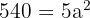
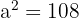
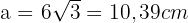
Mit KI zusammenfassen:


