Natürlichen Zahlen
Mit den natürlichen Zahlen zählen wir die Elemente einer Menge (Kardinalzahl). Oder wir drücken die Position oder Reihenfolge aus, die ein Element in einer Menge einnimmt (Ordnungszahl).
Die Menge der natürlichen Zahlen wird wie folgt gebildet:
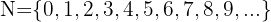
Die Summe und das Produkt zweier natürlicher Zahlen ergibt eine weitere natürliche Zahl.
Die Differenz zweier natürlicher Zahlen ist nicht immer eine natürliche Zahl, sondern nur dann, wenn der Minuend größer ist als der Subtrahend.
Beispiele
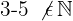
Der Quotient zweier natürlicher Zahlen ist nicht immer eine natürliche Zahl, sondern kommt nur vor, wenn die Division genau aufgeht.
Beispiele
Wir können Potenzen verwenden, da dies die abgekürzte Form ist, ein Produkt zu schreiben, das aus mehreren gleichen Faktoren besteht.
Die Wurzel einer natürlichen Zahl ist nicht immer eine natürliche Zahl, sondern nur, wenn die Wurzel vollständig ziehbar ist.
Ganze Zahlen
Ganze Zahlen sind vom Typ:
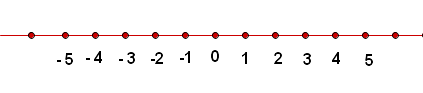
Sie ermöglichen es uns, Folgendes auszudrücken: geschuldetes Geld, Temperatur unter dem Gefrierpunkt, Höhe über dem Meeresspiegel usw.
Die Summe, die Differenz und das Produkt von zwei ganzen Zahlen ergibt eine weitere ganze Zahl.
Der Quotient zweier ganzer Zahlen ist nicht immer eine ganze Zahl, sondern nur, wenn die Division genau aufgeht.
Beispiele
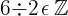
Wir können mit Potenzen rechnen, jedoch muss der Exponent eine natürliche Zahl sein.
Beispiele
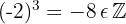
Die Wurzel einer ganzen Zahl ist nicht immer eine ganze Zahl, sondern nur dann, wenn die Wurzel exakt ist oder wenn es sich um einen Wurzelexponenten mit positivem Radikanden handelt.
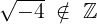
Rationale Zahlen
Eine rationale Zahl ist jede Zahl, die sich als Quotient zweier ganzer Zahlen mit einem Nenner ungleich 0 darstellen lässt.
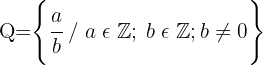
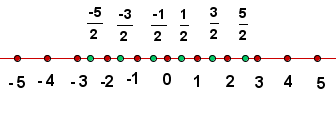
Die Dezimalzahlen (exakte Dezimalzahlen, rein periodische Zahlen und gemischt periodische Zahlen) sind rationale Zahlen; die anderen unbegrenzten Dezimalzahlen sind es nicht.
Die Summe, die Differenz, das Produkt und der Quotient zweier rationaler Zahlen ergibt eine weitere rationale Zahl.
Wir können mit Potenzen rechnen, jedoch muss der Exponent eine ganze Zahl sein.
Die Wurzel einer rationalen Zahl ergibt nicht immer eine rationale Zahl, sondern nur dann, wenn die Wurzel exakt ist, und wenn der Wurzelexponent gerade ist, muss der Radikand positiv sein.
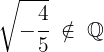
Irrationale Zahlen
Eine Zahl ist irrational, wenn sie unendlich viele nichtperiodische Nachkommastellen hat und daher nicht als Bruch ausgedrückt werden kann.
Die bekannteste irrationale Zahl ist 
, definiert als das Verhältnis der Länge des Umfangs zu seinem Durchmesser.
Weitere irrationale Zahlen sind:
Die Zahl 
taucht bei Wachstumsprozessen, beim radioaktiven Zerfall und in der Formel der Kettenline auf, der Kurve, die wir bei Stromleitungen sehen können.
Der goldene Schnitt, 
, wurde von Künstler aller Epcohen por artistas de todas las épocas (Fidias, Leonardo da Vinci, Alberto Durero, Dalí,..) für die Verhältnisse bei ihren Arbeiten verwendet.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
