Kapitel

Rückblick
Anmerkung: Jede reelle Zahl ist eine komplexe Zahl, aber nicht jede komplexe Zahl ist eine reelle Zahl.
Formeln für das Rechnen mit komplexen Zahlen:
Addition
Die reellen und imaginären Teile werden einerseits miteinander verbunden und addiert, andererseits die imaginären Teile.

Multiplikation
Erfolgt auf die gleiche Weise wie das Produkt aus 2 Binomen, unter Verwendung der Distributivität, wobei zu beachten ist, dass 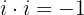
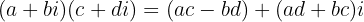
Division
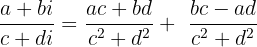
Arithmetik der komplexen Zahlen
Führe folgende Berechnungen durch:
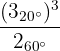
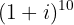


1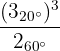
Zunächst erhöhen wir den Zähler auf die dritte Potenz.

Wir berechnen den Quotienten
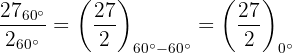
2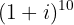
Wir wandeln die Zahl 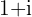 in die Polarform um
in die Polarform um
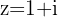
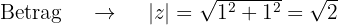
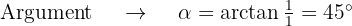
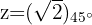
Schließlich berechnen wir die Potenz von 
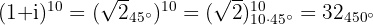
Wenn wir das Argument auf einen Winkel zwischen  und
und 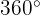 festlegen, erhalten wir
festlegen, erhalten wir

3
Wir wandeln die Zahl  in die Polarform um
in die Polarform um

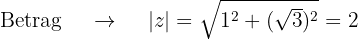
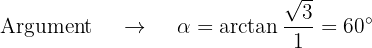

Schließlich berechnen wir die Potenz von 
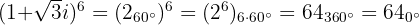
4
Wir wandeln den Zähler innerhalb der Wurzel in die Polarform um

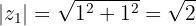
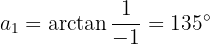

Nun wandeln wir den Nenner in die Polarform um
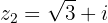
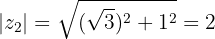
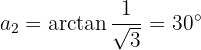

Wir berechnen den Quotienten
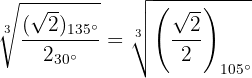
Obtenemos el módulo y el argumento de las raíces
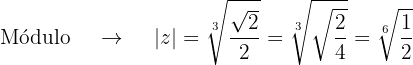
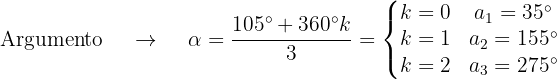
Las raíces terceras constan entonces de los números
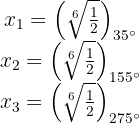
Löse 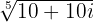 und drücke in Polarform aus
und drücke in Polarform aus
Wir wandeln die Zahl 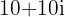 in die Polarform um
in die Polarform um

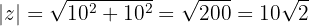
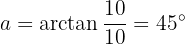
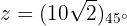
Somit
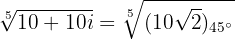
Um die Wurzeln zu berechnen, benötigen wir den Betrag und die Argumente
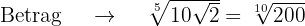
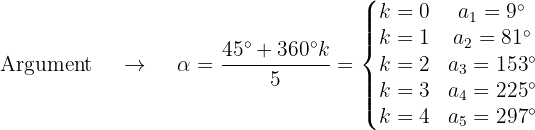
Die 5 fünften Wurzeln bestehen dann aus den Zahlen
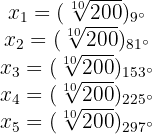
Berechne die folgende Rechenoperation und gib das Ergebnis in Polarform an.
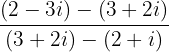
Wir entfernen die Klammern, um die Operationen im Zähler und Nenner durchführen zu können.

Wir multiplizieren den Zähler und den Nenner mit der Konjugierten des Letzteren
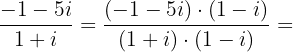
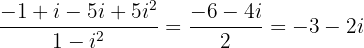
Somit

Für die Polarform ermitteln wir den Betrag und das Argument
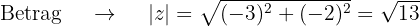
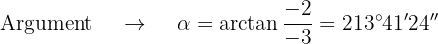
Und somit
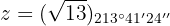
Berechne den Wert des Quotienten. Berechne die Kubikwurzeln und drücke sie in polarer, trigonometrischer und binomischer Form aus.
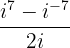
1Berechnung des Quotienten
Wir ändern den negativen Exponenten und berechnen
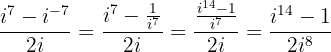
Wir beachten, dass 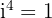 und erhalten
und erhalten
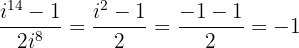
Somit
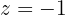
2In Polarform umwandeln
Um die Wurzeln von  zu erhalten, müssen wir in die Polarform umandeln. Hierzu benötigen wir den Betrag und das Argument
zu erhalten, müssen wir in die Polarform umandeln. Hierzu benötigen wir den Betrag und das Argument
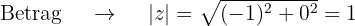
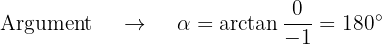
Und somit

3Berechnung der dritten Wurzeln
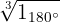
Wir berechnen den Betrag und das Argument der Wurzeln

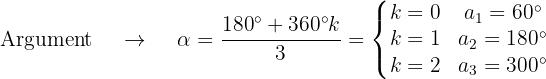
Die 3 Kubikwurzeln bestehen dann aus den Zahlen
4Wurzeln in trigonometrischer und binomischer Form
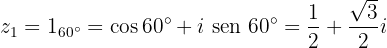
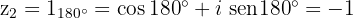
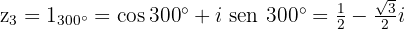
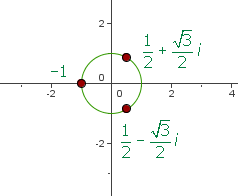
Wurzeln einer Gleichung
Berechne die Wurzeln der folgenden Gleichung: 
Wir bestimmen 
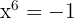
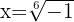
Wir ändern die Zahl innerhalb der Wurzel in die Polarform, in diesem Fall -1.
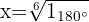
Wir berechnen den Betrag und das Argument der Wurzeln
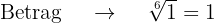
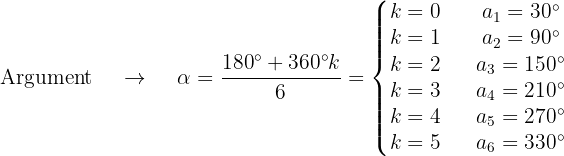
Die Wurzeln der Gleichung sind dann die Zahlen mit dem Betrag 1 und mit den oben genannten Argumenten, d. h,
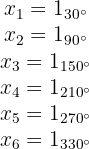
Berechne alle Wurzeln der Gleichung:
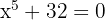
Wir bestimmen
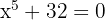

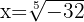
Wir ändern die Zahl innerhalb der Wurzel in die Polarform
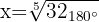
Wir berechnen den Betrag und das Argument der Wurzeln
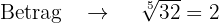
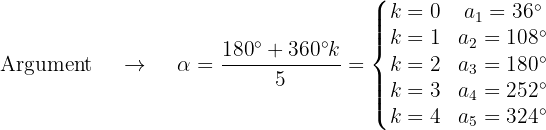
Die fünften Wurzeln bestehen dann aus den Zahlen
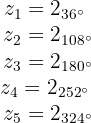
Schreibe eine quadratische Gleichung mit den Lösungen 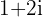 und ihrer Konjugierten.
und ihrer Konjugierten.
Gegeben ist eine komplexe Zahl und die Konjugierte
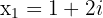

Wir können eine Gleichung zweiten Grades ermitteln, deren Lösungen diese Zahlen sind. Diese Gleichung wird wie folgt ausgedrückt
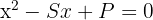
 ist die Summe der Wurzeln und
ist die Summe der Wurzeln und  das Produkt. In diesem Fall
das Produkt. In diesem Fall
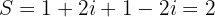
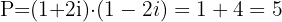
Die gesuchte Gleichung lautet also

Konjugiertes einer komplexen Zahl, Polarform und trigonometrische Form
Schreibe in polarer und trigonometrischer Form die Konjugierten und Gegenzahlen von:
1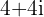
Wir berechnen den Betrag und das Argument der Wurzeln
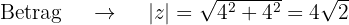
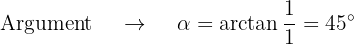
Dann wird  in polarer und trigonometrischer Form zu
in polarer und trigonometrischer Form zu
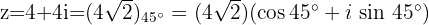
Die Konjugierte
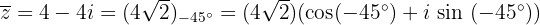
Die Gegenzahl
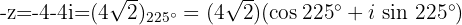
2 
Wir berechnen den Betrag und das Argument der Wurzeln
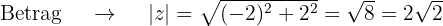
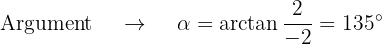
Dann wird  in polarer und trigonometrischer Form zu
in polarer und trigonometrischer Form zu
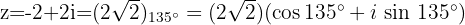
Die Konjugierte
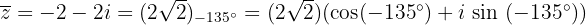
Die Gegenzahl
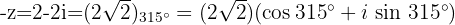
Satz von de Moivre und Binomischer Lehrsatz
Drücke in Polar- und Binomialform eine komplexe Zahl aus, die hoch 3 wie folgt ist:
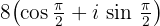
Wir wandeln in Polarform um
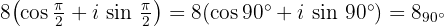
Gesucht ist eine Zahl  , deren Kubikzahl die obige Zahl ergibt
, deren Kubikzahl die obige Zahl ergibt

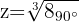
Wir berechnen den Betrag und das Argument der Wurzeln

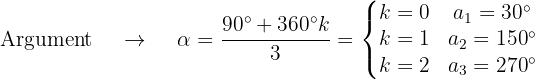
Die 3 Kubikwurzeln bestehen dann aus den Zahlen

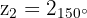
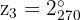
Umgerechnet in die trigonometrische und binomische Form erhält man
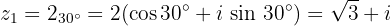
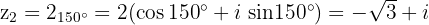
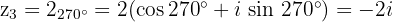
Gib in Funktion von cos α und sin α an:
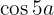
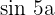
1 Binomischer Lehrsatz:
Wir wenden den Binomischen Lehrsatz an
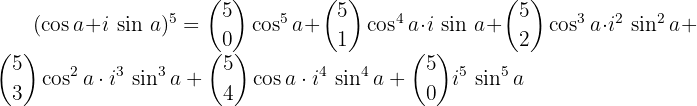
Wir berechnen
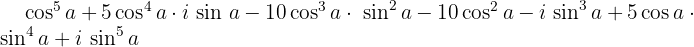
Wir teilen den Realteil und den Imaginärteil
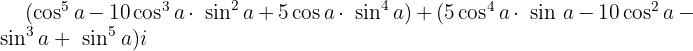
2 Satz von de Moivre:
Andererseits wissen wir, dass
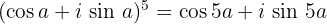
Unter Verwendung des Ergebnisses, das wir mit dem Binomischen Lehrsatz erzielt haben, setzen wir die Realteile gleich und erhalten
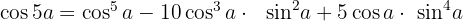
Wir setzen die Imaginärteile gleich und erhalten
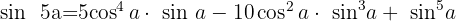
Drücke in Funktion von 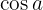 und
und 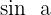 aus:
aus:
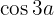
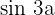
1 Binomischer Lehrsatz:
Wir wenden den Binomischen Lehrsatz an
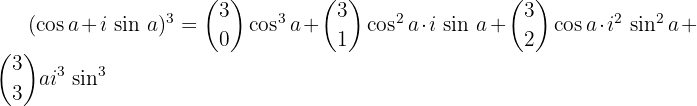
Wir berechnen
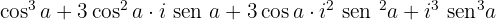
Wir teilen den Realteil und den Imaginärteil
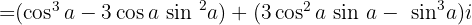
2 Satz von de Moivre:
Andererseits wissen wir, dass
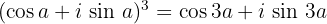
Unter Verwendung des Ergebnisses, das wir mit dem Binomischen Lehrsatz erzielt haben, setzen wir die Realteile gleich und erhalten

Wir setzen die Imaginärteile gleich und erhalten
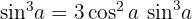
Mit KI zusammenfassen:












