Berechne  , so dass die komplexe Zahl, die wir durch die folgende Division erhalten, auf der Winkelhalbierenden des 1. Quadranten dargestellt wird
, so dass die komplexe Zahl, die wir durch die folgende Division erhalten, auf der Winkelhalbierenden des 1. Quadranten dargestellt wird
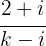
1 Damit sich der Koeffizient  der komplexen Zahl im 1. Quadranten befindet, muss gelten:
der komplexen Zahl im 1. Quadranten befindet, muss gelten:  . Wir multiplizieren Zähler und Nenner mit der Konjugierten des Nenners, um den Quotienten zu berechnen
. Wir multiplizieren Zähler und Nenner mit der Konjugierten des Nenners, um den Quotienten zu berechnen
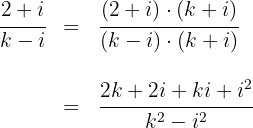
2 Wir schreiben den Realteil und den Imaginärteil und denken dabei daran, dass 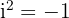
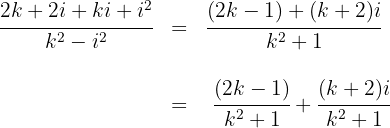
3 Wir setzen die beiden Teile gleich, da ihr Nenner gleich ist und somit auch ihr Zähler
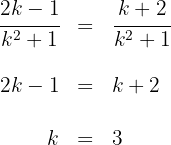
Somit ist der gesuchte Wert 
Ermittle den Wert von  , so dass der Quotient eine rein imaginäre Zahl und eine reelle Zahl ist
, so dass der Quotient eine rein imaginäre Zahl und eine reelle Zahl ist

1 Wir multiplizieren Zähler und Nenner mit der Konjugierten des Nenners, um den Quotienten zu berechnen

2 Wir schreiben den Realteil und den Imaginärteil und denken dabei daran, dass 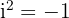
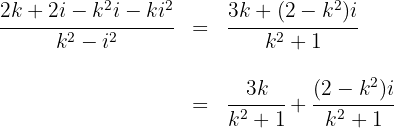
3 Um eine rein imaginäre Zahl zu erhalten, muss der Realteil gleich 0 sein
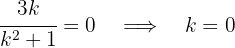
Damit die Zahl eine rein imaginäre Zahl ist, muss 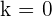 sein
sein
4 Um eine reelle Zahl zu erhalten, muss der Imaginärteil 0 sein

Damit also die Zahl eine reelle Zahl ist, muss  sein
sein
Wir nehmen die komplexe Zahl 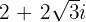 , die Zeiger der Uhr werden um
, die Zeiger der Uhr werden um  um den Koordiantenursprung gegen den Uhrzeigersinn gedreht. Berechne die komplexe Zahl, die man nach der Umdrehung erhält.
um den Koordiantenursprung gegen den Uhrzeigersinn gedreht. Berechne die komplexe Zahl, die man nach der Umdrehung erhält.
1 Wir schreiben eine Zahl in Polarform
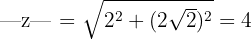
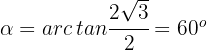
entonces 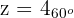
2 Wir multiplizieren mit einer komplexen Zahl vom Betrag 1 und Argument 
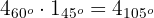
Die gesuchte Zahl ist 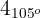
Ermittle die Koordinaten der Eckpunkte eines regelmäßigen Sechsecks, dessen Mittelpunkt im Koordinatenursprung liegt, wobei zu beachten ist, dass einer der Eckpunkte der Koeffizient der komplexen Zahl 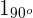 ist.
ist.
1 Die Eckpunkte sind die Koeffizienten der 6. Wurzel einer anderen komplexen Zahl 

2 Wir berechnen die 6. Wurzeln

3 Wir berechnen die Werte für 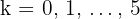
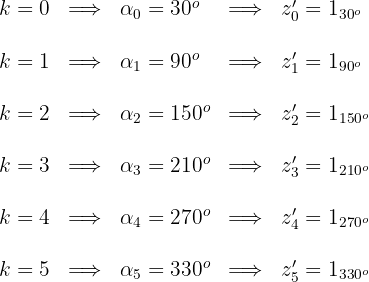
4 Die gesuchten Koordinaten sind
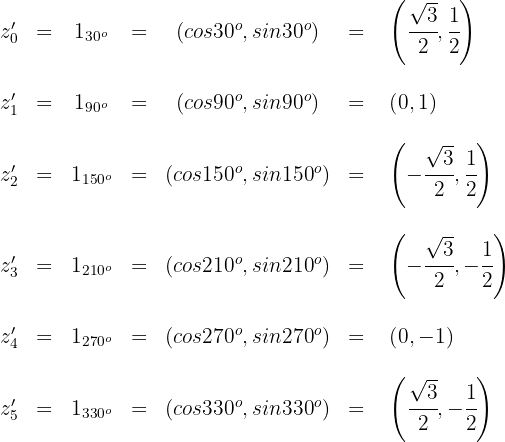
Ermittle den Wert von  und
und  , so dass der Quotient
, so dass der Quotient 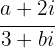 gleich
gleich 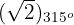 ist
ist
1 Wir drücken 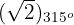 als komplexe Zahl aus
als komplexe Zahl aus
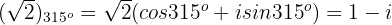
2 Wir setzen den Quotienten mit dem vorherigen Ausdruck gleich, multiplizieren beide Seiten mit  und lösen
und lösen
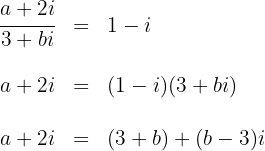
3 Wir setzen den Imaginärteil beider Seiten gleich und erhalten

4 Wir setzen den Realteil beider Seiten gleich und erhalten

Wie lauten die Koordinaten des Punktes, den man erhält, wenn man den Koeffizienten der komplexen Zahl 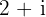 gegen den Uhrzeigersinn
gegen den Uhrzeigersinn  um den Ursprung dreht?
um den Ursprung dreht?
1 Wir wissen, dass

2 Wir multiplizieren mit der komplexen Zahl vom Betrag 1 und Argument 
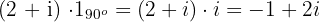
Die gesuchten Koordinaten sind 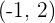
Ermittle die Koordinaten der Eckpunkte eines Quadrats, dessen Mittelpunkt im Koordinatenursprung liegt, wobei einer der Eckpunkte der Punkt  ist.
ist.
1 Wir schreiben  in Polarform
in Polarform
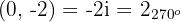
2 Die Eckpunkte sind die Koeffizienten der 4. Wurzeln einer anderen komplexen Zahl 
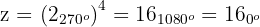
3 Wir berechnen die 4. Wurzeln
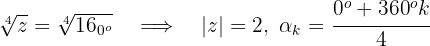
4 Wir berechnen die Werte für 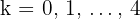
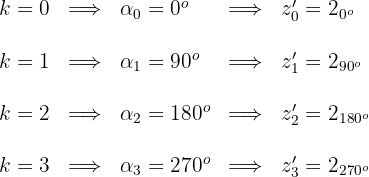
5 Die gesuchten Koordinaten sind
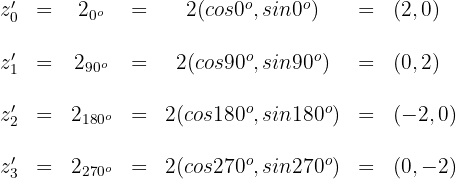
Die Summe der Realteile zweier konjugierter komplexer Zahlen ist 6, und die Summe ihrer Beträge ist 10. Ermittle diese komplexen Zahlen in Binom- und Polarform.
1 Wir schreiben die komplexe Zahl  in Polarform
in Polarform
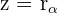
2 Wir schreiben ihre konjugierte Zahl  in Polarform
in Polarform
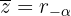
3 Die Summe der Realteile ist 6. Daraus erhalten wir
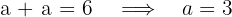
4 Die Summe der Beträge ist 10. Daraus erhalten wir

5 Aus dem Ausdruck des Betrags  ergibt sich
ergibt sich

5 Wir berechnen das Argument
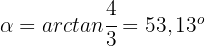
Somit lauten die komplexen Zahlen
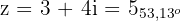
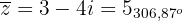
Mit KI zusammenfassen:


