Definition einer Folge
Eine Folge ist eine geordnete Menge von Zahlen, die als Glieder bezeichnet werden und durch einen Buchstaben und ein tiefgestelltes Zeichen für den Platz, den sie einnehmen, gekennzeichnet sind.
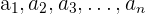
Beispiel: 
Die Zahlen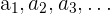 
werden Glieder einer Folge genannt.
Der tiefgestellte Index gibt den Platz an, den das Glied in der Folge einnimmt.
Das allgemeine Glied 
ist ein Kriterium, mit dem man jedes Glied der Folge bestimmen kann.
Eine Folge wird normalerweise in geschweiften Klammern ausgedrückt: 
oder in runden Klammern 
Eine Folge bestimmen
Anhand des allgemeinen Gliedes
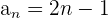
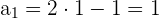
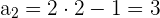
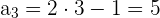
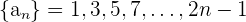
Nicht alle Folgen haben ein allgemeines Glied:
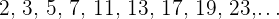
Anhand der Rekursion
Die Gliederungen ergeben sich aus den vorangegangenen Gliedern.
Schreibe eine Folge, deren erstes Glied 2 ist, wobei jedes Glied das Quadrat des vorhergehenden Gliedes ist.
Fibonacci-Folge:
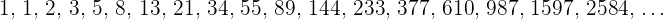
Die ersten beiden Glieder sind Einsen, die anderen ergeben sich aus der Addition der beiden vorherigen Glieder.
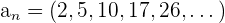
Rechnen mit Folgen
Gegeben sind die Folgen und 
:
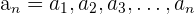
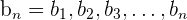
Addition von Folgen
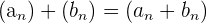
Gesetze
1 Assoziativ:
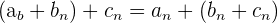
2 Kommutativ:
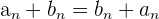
3 Neutrales Element
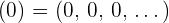
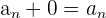
4 Gegensätzliche Folge
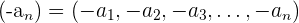
Subtraktion von Folgen
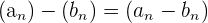
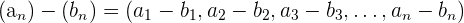
Produkt aus Folgen
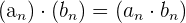
Gesetze
1 Assoziativ:
2 Kommutativ:
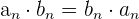
3 Neutrales Element
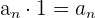
4 Distributiv in Bezug auf die Summe
Umkehrfolge
Eine Folge ist invertierbar oder umkehrbar, wenn alle ihre Glieder ungleich 0 sind. Wenn die Folge umkehrbar ist, lautet ihre Umkehrfolge:
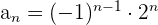
Quotient von Folgen
Der Quotient aus zwei Folgen ist nur möglich, wenn der Nenner umkehrbar ist.
Arten von Folgen
Monotone Folgen
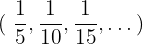
Streng monoton steigende Folgen
Eine Folge ist streng monoton steigend, wenn jedes Glieder größer als das vorherige Glied ist.
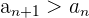
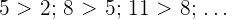
Monoton steigende Folgen
Eine Folge ist monoton steigend, wenn sie von Glied zu Glied gleich bleibt oder zunimmt.
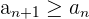
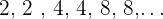
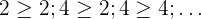
Streng monoton fallende Folgen
Eine Folge ist streng monoton fallend, wenn sie von Glied zu Glied abnimmt.
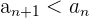
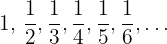
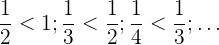
Monton fallende Folgen
Eine Folge ist monoton fallend, wenn sie von Glied zu Glied gleich bleibt oder abnimmt.
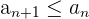
Konstante Folgen
Eine Folge ist konstant, wenn alle ihre Glieder übereinstimmen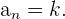 
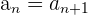
Nach unten beschränkte Folgen
Eine Folge ist nach unten beschränkt, wenn alle ihre Glieder größer oder gleich einer bestimmten Zahl K sind, die wir die untere Schranke der Folge nennen.
Die größte untere Schrankte wird Infimum genannt.
Wenn das Infimum einer Folge eines ihrer Glieder ist, nennt man es Minimum.
Jede monoton steigende und nach oben beschränkte Folge ist konvergent und ihr Grenzwert ist gleich dem Supremum der Folge.
Nach oben beschränkte Folgen
Eine Folge ist nach oben beschränkt, wenn alle ihre Glieder kleiner oder gleich einer bestimmten Zahl K' sind, die wir die obere Schranke der Folge nennen.
Die kleinste der oberen Schranken wird als Supremum bezeichnet.
Konvergente Folgen sind Folgen, die einen endlichen Grenzwert haben.
Wenn das Supremum einer Folge eines ihrer Glieder ist, nennt man es Maximum.
Jede streng monoton fallende Folge und nach unten beschränkte Folge ist konvergent und ihr Grenzwert ist gleich dem Infimum der Folge.
Beschränkte Folgen
Eine Folge gilt als beschränkt, wenn sie nach oben und unten beschränkt ist. Das heißt, wenn es eine Zahl k gibt, die kleiner oder gleich allen Gliedern der Folge ist, und eine andere K', die größer oder gleich allen Gliedern der Folge ist. Alle Glieder der Folge liegen also zwischen k und K'.
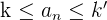
Konvergente Folgen
Konvergente Folgen haben einen endlichen Grenzwert.
Grenzwert = 0
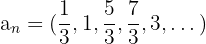
Grenzwert = 1
Divergente Folgen
Divergente Folgen sind Folgen, die keinen endlichen Grenzwert haben.
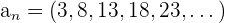
Grenzwert = 
Oszillierende Folgen
Oszillierende Folgen sind weder konvergent noch divergent. Ihre Glieder alternieren zwischen dem größten und dem kleinsten Glied oder umgekehrt.
Alternierende Folgen
Alternierende Folgen sind solche, bei denen sich die Vorzeichen der Glieder abwechseln. Diese können sein:
Konvergent
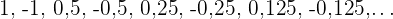
Sowohl die geraden als auch die ungeraden Glieder konvergieren gegen den Grenzwert 0.
Divergent
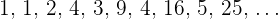
Sowohl die geraden als auch die ungeraden Glieder konvergieren gegen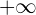 
.
Oszillierend
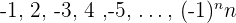
Beispiele:
1 
Steigend.
Nach unten beschränkt
Untere Schranken: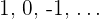 
Das Minimum ist 1.
Nicht nach oben beschränkt.
Divergent
2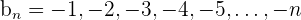 
Fallend.
Nach oben beschränkt
Obere Schranken: 
Das Maximum ist –1.
Nicht nach unten beschränkt.
Divergent.
3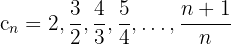 
Fallend.
Nach oben beschränkt
Obere Schranken: 
Das Maximum ist 2.
Nach unten beschränkt
Untere Schranken: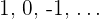
Das Infimum ist 1.
Konvergent, Grenzwert = 1.
4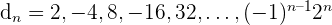 
Nicht monoton.
Nicht beschränkt.
Nicht konvergent, nicht divergent.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
