Kapitel
Wir erklären, was der unbestimmte Ausdruck "0 mal unendlich" ist und wie diese Art der Unbestimmtheit mit anderen unbestimmten Ausdrücken gleichzusetzen ist.

sowie 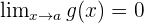 und
und  . Unsere Funktion, ausgewertet für
. Unsere Funktion, ausgewertet für  , wäre also
, wäre also
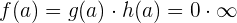
In diesem Fall sagen wir, dass die Funktion bei  unbestimmt ist, da es nicht möglich ist,
unbestimmt ist, da es nicht möglich ist,  einen beliebigen Wert zuzuordnen. Wir können jedoch eine der folgenden Methoden anwenden, um den Grenzwert der Funktion bei
einen beliebigen Wert zuzuordnen. Wir können jedoch eine der folgenden Methoden anwenden, um den Grenzwert der Funktion bei  zu finden – beachet, dass der Grenzwert bei
zu finden – beachet, dass der Grenzwert bei  nicht mit dem Wert von
nicht mit dem Wert von  identisch ist. – :
identisch ist. – :
Der unbestimmte Ausdruck 0 mal unendlich lässt sich am besten vermeiden, indem man ihn in einen unbestimmten Ausdruck der Form unendlich geteilt durch unendlich oder 0 geteilt durch 0 umwandelt.

Unbestimmten Ausdruck in unendlich geteilt durch unendlich umwandeln
Wenn  gegen
gegen  konvergiert, wenn
konvergiert, wenn  gegen
gegen  konvergiert, gilt, dass
konvergiert, gilt, dass 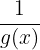 gegen
gegen  konvergiert, wenn
konvergiert, wenn  gegen
gegen  konvergiert. Als Gleichungen geschrieben:
konvergiert. Als Gleichungen geschrieben:
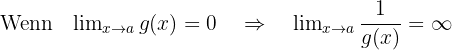 .
.
So können wir die ursprüngliche Funktion  wie folgt schreiben:
wie folgt schreiben:
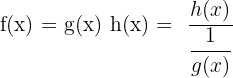 ,
,
Wir berechnen den Grenzwert und erhalten
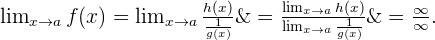
Nachdem der unbestimmte Ausdruck in 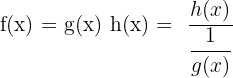 umgewandelt wurde, können wir wie im Artikel unendlich geteilt durch unendlich beschrieben vorgehen
umgewandelt wurde, können wir wie im Artikel unendlich geteilt durch unendlich beschrieben vorgehen
Beispiele:
1. 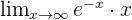
In diesem Beispiel haben wir die Funktion
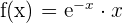 .
.
Wir möchten den Grenzwert  berechnen. Wir stellen fest, dass
berechnen. Wir stellen fest, dass 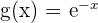 und
und 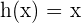 . Somit haben wir
. Somit haben wir 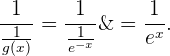
Da ein Exponentialausdruck viel schneller wächst als ein Polynom, bedeutet dies, dass 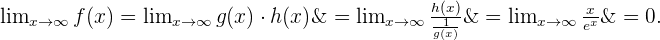
2. 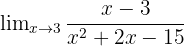
In diesem Beispiel haben wir die Funktion
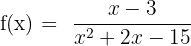 .
.
Wir möchten den Grenzwert 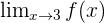 berechnen. Wir analysieren den Nenner der Funktion
berechnen. Wir analysieren den Nenner der Funktion  und stellen fest, dass
und stellen fest, dass 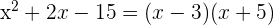 . Also können wir die Funktion
. Also können wir die Funktion  wie folgt schreiben:
wie folgt schreiben:
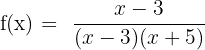 .
.
Wir stellen fest, dass  und
und 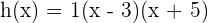 . Somit erhalten wir
. Somit erhalten wir 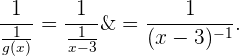
Somit wäre  gleich
gleich 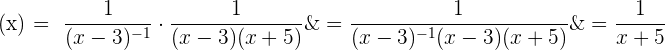
Wir berechnen den Grenzwert und erhalten 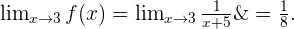
Unbestimmten Ausdruck 0 geteilt durch 0 umwandeln
Wenn  gegen
gegen  konvergiert, wenn
konvergiert, wenn  gegen
gegen  konvergiert, konvergiert
konvergiert, konvergiert 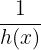 gegen 0, wenn
gegen 0, wenn  gegen
gegen  konvergiert. Wir schreiben die Gleichungen wie folgt:
konvergiert. Wir schreiben die Gleichungen wie folgt:
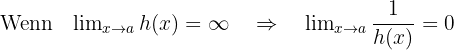 .
.
Somit können wir die ursprüngliche Funktion  wie folgt schreiben:
wie folgt schreiben:
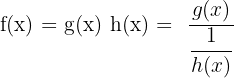 ,
,
Wir berechnen den Grenzwert und erhalten 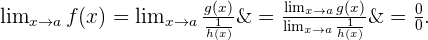
Sobald wir den unbestimmten Ausdruck umgewandelt haben 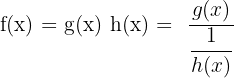 , können wir wie im Artikel 0 geteilt durch 0 vorgehen
, können wir wie im Artikel 0 geteilt durch 0 vorgehen
Beispiele:
1. 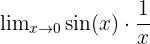
In diesem Beispiel haben wir die Funktion
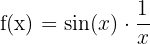 .
.
Wir möchten den Grenzwert  berechnen. Wir stellen fest, dass
berechnen. Wir stellen fest, dass 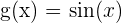 und
und 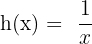 . So können wir
. So können wir  wie folgt schreiben:
wie folgt schreiben:
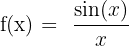
Wir erhalten den unbestimmten Ausdruck 0 geteilt durch 0. Um dies zu lösen, wenden wir die Regel von de L’Hospital an und erhalten 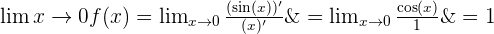
2. 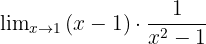
In diesem Beispiel haben wir die Funktion
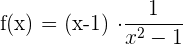 .
.
Wir möchten den Grenzwert 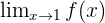 berechnen. Wir analysieren den Nenner der Funktion
berechnen. Wir analysieren den Nenner der Funktion  und können sehen, dass
und können sehen, dass 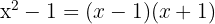 . Somit können wir
. Somit können wir  wie folgt schreiben
wie folgt schreiben
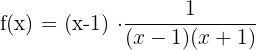 .
.
Wir stellen fest, dass 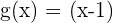 und
und 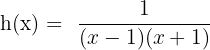 . Also wäre
. Also wäre  gleich
gleich 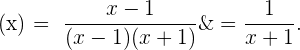
Wir berechnen den Grenzwert und erhalten 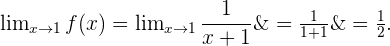
Mit KI zusammenfassen:












