
Formel für die partielle Integration
Einleitung
Im Gegensatz zu den Ableitungen gibt es keine Formel für die Integration eines Produkts von Funktionen.
Das, was einer Regel für die Integration des Produkts von Funktionen am nächsten kommt, ist die partielle Integration. Interessanterweise basiert sie auf der Formel für die Ableitung eines Produkts von Funktionen.
Bei der partiellen Integration wird jedoch ein Integral eines Produkts in ein anderes Integral umgewandelt. Diese Formel funktioniert nicht für die Integration aller Produkte von Funktionen.
Die Formel für die partielle Integration lautet

Man beachte, dass wir  ableiten und
ableiten und  integrieren müssen. Daher ist es praktisch, dass das Integral von
integrieren müssen. Daher ist es praktisch, dass das Integral von  vereinfacht ist.
vereinfacht ist.
Im Allgemeinen werden Polynom-, Logarithmus- und Arkustangensfunktionen als  gewählt. Exponential-, Sinus- und Kosinusfunktionen werden als
gewählt. Exponential-, Sinus- und Kosinusfunktionen werden als  gewählt.
gewählt.
Herleitung der Formel
Angenommen, wir haben die Funktionen  und
und  . Dann ist ihre Ableitung gegeben durch
. Dann ist ihre Ableitung gegeben durch

Wenn wir beide Seiten der Gleichung integrieren, erhalten wir
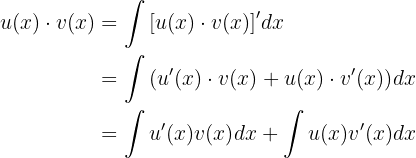
Wenn wir  auf die linke Seite bringen, erhalten wir
auf die linke Seite bringen, erhalten wir
 ,
,
was die gesuchte Formel ist.
Aufgaben

Wir haben ein Produkt aus der Funktion 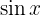 und
und  . Wie oben erwähnt, werden in solchen Fällen
. Wie oben erwähnt, werden in solchen Fällen 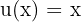 und
und 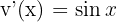 gewählt.
gewählt.
Wir leiten  ab:
ab:
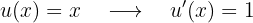
Wir integrieren  :
:
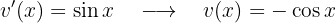
Das Integral lautet also wie folgt
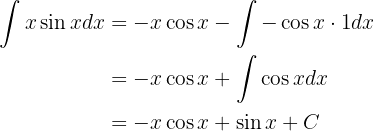
Somit
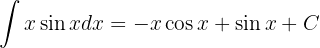

Wir haben ein Produkt aus der Funktion  und
und  . In diesem Fall wählen wir
. In diesem Fall wählen wir 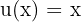 und
und  .
.
Wir leiten  ab:
ab:
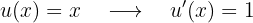
Wir integrieren  :
:

Das Integral lautet also wie folgt
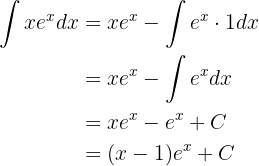
Somit
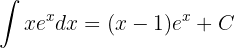
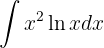
Wir haben ein Produkt aus der Funktion 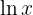 und
und  . Im Allgemeinen wird bei beiden Funktionen
. Im Allgemeinen wird bei beiden Funktionen  gewählt; In diesem Fall hat jedoch der Logarithmus Vorrang und wir wählen
gewählt; In diesem Fall hat jedoch der Logarithmus Vorrang und wir wählen  und
und 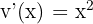 .
.
Wir leiten  ab (deshalb wählen wir den Logarithmus):
ab (deshalb wählen wir den Logarithmus):
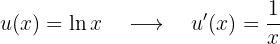
Wir integrieren  :
:
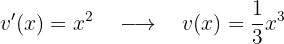
Das Integral lautet also wie folgt
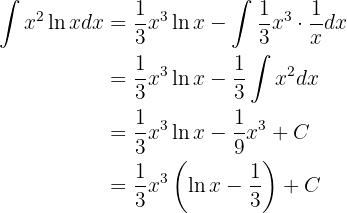
Somit
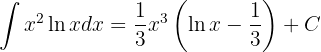
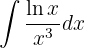
Wir haben ein Produkt aus der Funktion 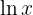 und
und 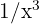 . In diesem Fall wählen wir wieder
. In diesem Fall wählen wir wieder  y
y 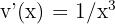 (die Logarithmusfunktion wird immer als
(die Logarithmusfunktion wird immer als  gewählt).
gewählt).
Wir leiten  ab:
ab:
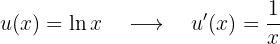
Wir integrieren  :
:
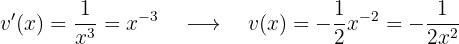
Das Integral lautet also wie folgt
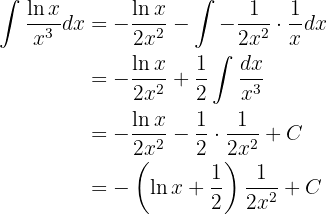
Somit
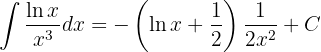
Mit KI zusammenfassen:












