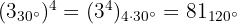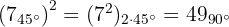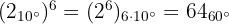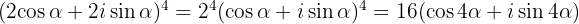Kapitel

Potenz komplexer Zahlen in Polarform
Die n-te Potenz 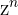 einer komplexen Zahl
einer komplexen Zahl  ist eine weitere komplexe Zahl, sodass:
ist eine weitere komplexe Zahl, sodass:
- Ihren Betrag erhält man, indem man den Betrag von
 hoch
hoch  nimmt
nimmt - Ihr Argument ist
 Mal das Argument von
Mal das Argument von 
Wenn die Zahl in polarer Form ausgedrückt wird, lassen sich ihre Potenzen sehr einfach berechnen, denn:
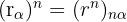
Beispiele:
Satz von de Moivre
Aus der vorherigen Formel können wir ableiten, dass 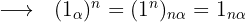
Wenn man dies trigonometrisch ausdrückt, ergibt sich der Satz von Moivre: 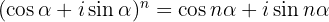
Dieser ist nützlich, wenn wir Potenzen komplexer Zahlen in trigonometrischer Form bilden.
Beispiele:
Aufgaben mit Potenzen komplexer Zahlen
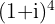
Es ist ratsam, 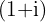 in die Polarform umzuwandeln.
in die Polarform umzuwandeln.
Betrag von 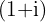
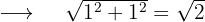
Argument von 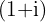
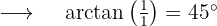
Wir wenden die Formel für Potenzen in Polarform an und erhalten
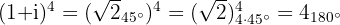
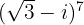
Es ist ratsam,  in die Polarform umzuwandeln.
in die Polarform umzuwandeln.
Betrag von 
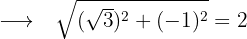
Arg. von 

Wir wenden die Formel für Potenzen in Polarform an und erhalten
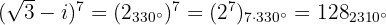
Allerdings  und somit
und somit 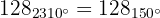
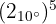
Die Polarform ist bereits gegeben, weshalb wir nur noch die Formel anwenden müssen
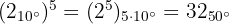
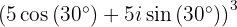
Wir möchten die Potenz einer komplexen Zahl in trigonometrischer Form erhalten.
Wir faktorisieren die  und erhalten so
und erhalten so

Wir wenden den Satz von de Moivre an und berechnen
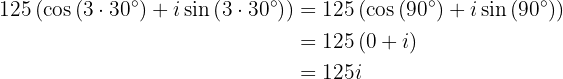
Mit KI zusammenfassen: