Kapitel

Definition des Prismas
Ein Prisma ist ein Polyeder mit zwei parallelen und gleichen Flächen, die als Grundflächen bezeichnet werden, und dessen Seitenflächen Parallelogramme sind.
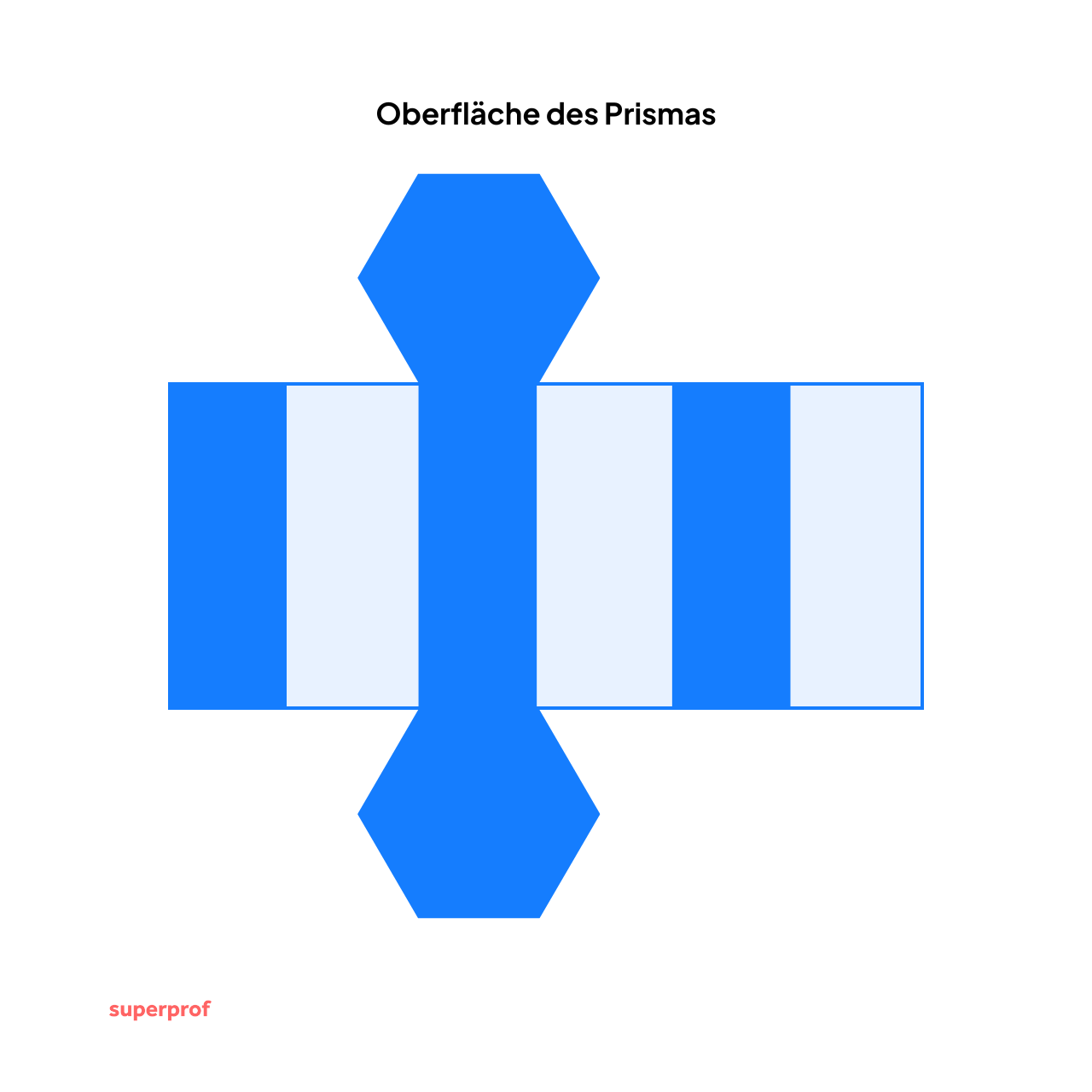
Die Oberfläche eines Prismas
Die Oberfläche eines Prismas erhält man, wenn man das Prisma „aufklappt”.
Elemente eines Prismas
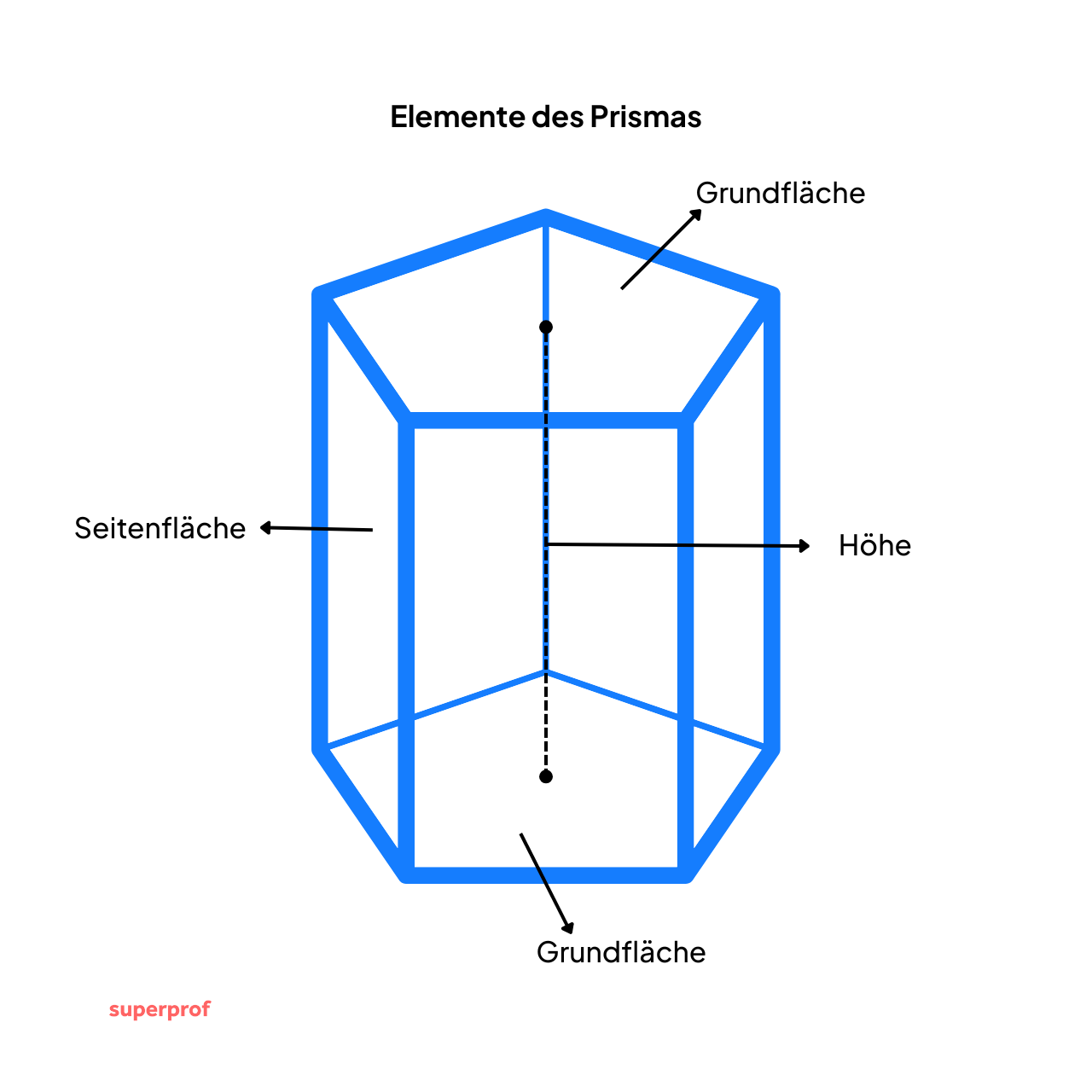
Die Höhe eines Prismas ist der Abstand zwischen den Grundflächen.
Die Seiten der Grundflächen bilden die Grundkanten und die Seiten der Seitenflächen die Seitenkanten, diese sind gleich und parallel zueinander.
Bei einem Prisma sind die Grundflächen kongruent, d. h. es handelt sich um Polygone mit derselben Anzahl von Seiten und denselben Maßen.
Flächeninhalt und Volumen eines Prismas
Im Allgemeinen ist die Mantelfläche eines Prismas die Summe der Flächen der Seitenflächen eines Prismas, und die Gesamtfläche eines Prismas ist die Summe der Flächen aller Flächen des Prismas (Grundflächen und Mantelfläche).

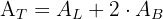
Das Volumen eines Prismas erhält man durch Multiplikation der Grundfläche  mit der Höhe
mit der Höhe  des Prismas.
des Prismas.

Arten von Prismen
Regelmäßige Prismen
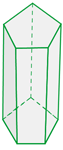
Es handelt sich um Prismen, deren Grundflächen regelmäßige Polygone sind.
Unregelmäßige Prismen
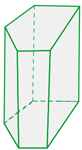
Es handelt sich um Prismen, deren Grundflächen unregelmäßige Polygone sind.
Rechtwinklige Prismen
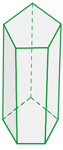
Es handelt sich um Prismen, deren Seitenflächen Rechtecke oder Quadrate sind.
Schiefe Prismen
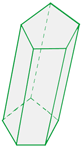
Es handelt sich um Prismen, deren Seitenflächen Parallelogramme oder Rauten sind.
Parallelepipede
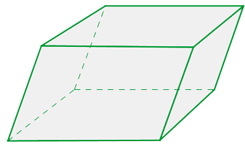
Parallelepipede sind Prismen, deren Grundflächen Parallelogramme sind.
Oktaeder
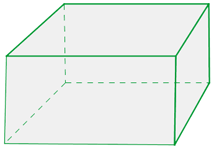
Orthoeder sind Parallelepipede, deren Flächen alle rechteckig sind.
Arten von Prismen nach ihrer Grundfläche
Dreiecksprisma
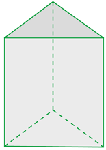
Ihre Grundflächen sind Dreiecke.
Quadratisches Prisma
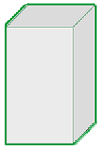
Seine Grundflächen sind Quadrate.
Fünfeckiges Prisma
Seine Grundflächen sind Fünfecke.
Sechseckiges Prisma

Seine Grundflächen sind Sechsecke.
Beispielaufgabe zu Prismen
1 Berechne die Höhe eines Prismas mit einer Grundfläche von 12 dm² und einem Volumen von 48 l.

Das Volumen berechnen wir wie folgt:

Wir berechnen die Höhe 'h'

Wir setzen die Werte ein und lösen

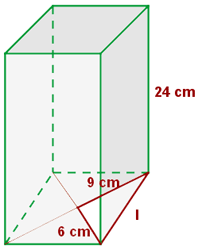
2 Berechne die Mantelfläche, die Gesamtfläche und das Volumen eines Prismas, dessen Grundfläche eine Raute mit den Diagonalen der Länge 12 y 18 cm ist.

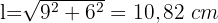
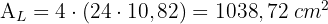
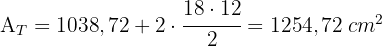

Mit KI zusammenfassen:












