Multiplikation von Wurzeln mit gleichem Wurzelexponenten
Um Wurzeln mit gleichem Wurzelexponenten zu multiplizieren, werden die Radikanden multipliziert und der gleiche Wurzelexponent beibehalten.
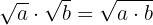
Beispiel für die Multiplikation von Wurzeln
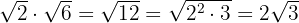
Wenn wir eine Rechenoperation abgeschlossen haben, werden wir, wenn möglich, Faktoren aus der Wurzel herausziehen.
Wurzeln gleichnamig machen
Zunächst ermitteln wir das kleinste gemeinsame Vielfache der Wurzelexponenten. Dies ist dann der gemeinsame Wurzelexponent.
Wir dividieren den gemeinsamen Wurzelexponenten durch jeden der Wurzelexponenten und jedes erzielte Ergebnis wird mit den entsprechenden Exponenten multipliziert.
Wir bringen sie zunächst auf einen gemeinsamen Wurzelexponenten und multiplizieren sie dann.
Beispiele für das Gleichnamigmachen von Wurzeln mit unterschiedlichem Wurzelexponenten
1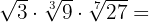 
Wir zerlegen die Radikanden in Faktoren
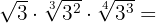
Wir ermitteln den gemeinsamen Wurzelexponenten. Hierfür berechnen wir das kgV der Wurzelexponenten. Dies ist dann der gemeinsame Wurzelexponent.
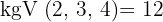
Wir dividieren den gemeinsamen Wurzelexponenten 
mit jedem der Wurzelexponenten 
und jedes erhaltene Ergebnis wird mit den entsprechenden Exponenten 
multipliziert
Wir bilden das Produkt der Potenzen mit derselben Basis im Radikanden und ziehen Faktoren aus dem Radikanden
2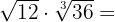 
Wir berechnen das kleinste gemeinsame Vielfache der Wurzelexponenten
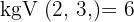
Wir dividieren den gemeinsamen Wurzelexponenten 
mit jedem der Wurzelexponenten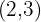 
und jedes erhaltene Ergebnis wird auf die entsprechenden Radikanden erhöht
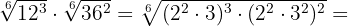
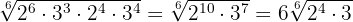
Wir zerlegen die und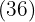 
in Faktoren, führen die Rechenoperationne mit den Potenzen durch und extrahieren Faktoren.
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
Im Rahmen einer Internetrecherche zu mathematischen Themen bin ich zufällig auf diese Seite gestoßen.Hier fielen mir Unstimmigkeiten auf: bei den ersten vier Beispielen liegen offensichtlich Formatierungsfehler vor, die sehen nämlich so aus:
„5-3∈ℕ3-5∉ℕ“, „6÷2∈ℕ2÷6∉ℕ“ „6÷2∈ℤ2÷6∉ℤ“ und „(-2)³=-8∈ℤ(-2)⁻³=-⅛∉ℤ“
das kann niemand lesen. Vermutlich fehlt jeweils ein Zeilenvorschub. Oder man schreibt was dazwischen, z.B. ein „aber“:
„5-3∈ℕ aber: 3-5∉ℕ“, „6÷2∈ℕ aber: 2÷6∉ℕ“ „6÷2∈ℤ aber: 2÷6∉ℤ“ und „(-2)³=-8∈ℤ aber: (-2)⁻³=-⅛∉ℤ“
So wäre es verständlich.
Jetzt aber zur Hauptsache: eigentlich ist alles ordentlich und korrekt erklärt. Nur, bei „rationale Zahlen“ steht da:
„““Rationale Zahlen
Eine rationale Zahl ist jede Zahl, die sich als Quotient zweier ganzer Zahlen … darstellen lässt.“““
völlig korrekt, aber im Abschnitt danach:
„““Irrationale Zahlen
Eine Zahl ist irrational, wenn sie unendlich viele nichtperiodische Nachkommastellen …“““
Das passt nicht zusammen, und der Sinn des Begriffs „irrationale Zahl“ bleibt unverständlich. Ja, im formallogischen Sinn kann man sagen „Eine Zahl ist irrational, wenn sie unendlich viele nichtperiodische Nachkommastellen hat und daher nicht als Bruch ausgedrückt werden kann“ – nur wirkt das wie „von hinten durch die Brust ins Auge“. Ich empfehle doch sehr, diesen Satz zu ändern in „Eine irrationale Zahl ist eine Zahl, die sich nicht als Quotient zweier ganzer Zahlen darstellen lässt. Ihre Dezimaldarstellung hat daher unendlich viele nichtperiodische Nachkommastellen“ Dann harmoniert das auch mit dem Abschnitt davor:
Rationale Zahlen – Eine rationale Zahl ist eine Zahl, die sich als Quotient zweier ganzer Zahlen … darstellen lässt.
Irrationale Zahlen – Eine rationale Zahl ist eine Zahl, die sich als Quotient zweier ganzer Zahlen darstellen lässt.
Vielen Dank für die Hinweise. Wir haben die Vorschläge gerne angenommen und im Artikel aktualisiert.