Kapitel

Definition: Rang einer Matrix
Der Rang einer Matrix ergibt sich aus der Zahl ihrer linear unabhängigen Zeilen (oder Spalten) an. Mithilfe dieser Definition läßt sich der Rang anhand des Gauß-Verfahrens lösen.
Der Rang einer Matrix lässt sich ebenso als Rang ihrer größten quadratischen Untermatrix definieren, die ungleich Null ist. Nach dieser Definition lässt sich der Rang einer Matrix mithilfe von Determinanten berechnen.
Die Zahl wird dabei lediglich als Rang von  (Matrix
(Matrix  ) bezeichnet und als Rang
) bezeichnet und als Rang 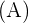 dargestellt.
dargestellt.
Wie berechnet man den Rang einer Matrix mithilfe von Determinanten?
Da der Rang dem der größten Untermatrix ungleich Null entspricht, werden folgende Rechenschritte durchgeführt, um den Rang der Determinante herauszufinden:
1 Entferne alle Zeilen (oder Spalten), die eine der folgenden Bedingungen erfüllen:
Alle Koeffizienten sind gleich Null,
Es gibt zwei gleiche Zeilen (oder Spalten).
Eine Zeile (oder Spalte) ist proportional zu einer anderen.
Eine Zeile (oder Spalte) ist eine Linearkombination anderer.
2 Wenn mindestens ein Element der Matrix nicht Null ist, ist auch ihre Determinante nicht Null, das heißt, der Rang ist größer oder gleich  .
.
3 Der Rang ist größer oder gleich  , wenn es eine quadratische Untermatrix
, wenn es eine quadratische Untermatrix 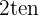 Ranges gibt, deren Determinante nicht Null ist.
Ranges gibt, deren Determinante nicht Null ist.
4 Der Rang ist größer oder gleich wenn es eine quadratische Untermatrix
wenn es eine quadratische Untermatrix 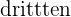 Ranges gibt, deren Determinante nicht Null ist.
Ranges gibt, deren Determinante nicht Null ist.
5 Der Rang ist größer oder gleich  , wenn es eine quadratische Untermatrix
, wenn es eine quadratische Untermatrix 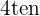 Ranges gibt, deren Determinante nicht Null ist.
Ranges gibt, deren Determinante nicht Null ist.
So fortfolgend wird Zahl für Zahl geprüft, ob die Matrix einen höheren Rang als  besitzt, bis die Untermatrix (oder die Untermatrizen) der höchstmöglichen Ordnung eine Nulldeterminante hat/haben.
besitzt, bis die Untermatrix (oder die Untermatrizen) der höchstmöglichen Ordnung eine Nulldeterminante hat/haben.
Berechnung des Rangs einer Matrix mithilfe von Determinanten: Beispiel
1 Gegeben sei eine Matrix  . Berechne ihren Rang
. Berechne ihren Rang  .
.

Lösung:
Den Definitionen zufolge, können folgende Rechenschritte durchgeführt werden:
1 Schließe die dritte Spalte aus, da sie eine Linearkombination der beiden ersten ist: .
.
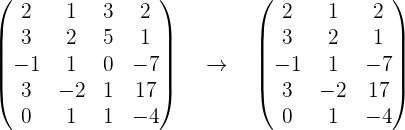
2 Prüfe ob der Rang größer oder gleich ist. Dafür muss mindestens ein Element der Matrix nicht Null sein, damit die Determinante nicht Null ist.
ist. Dafür muss mindestens ein Element der Matrix nicht Null sein, damit die Determinante nicht Null ist.
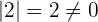
3 Der Rang der Matrix istgrößer oder gleich , wenn es eine quadratische Untermatrix
, wenn es eine quadratische Untermatrix 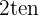 Ranges gibt, deren Determinante nicht Null ist.
Ranges gibt, deren Determinante nicht Null ist.
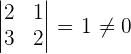
4 Der Rang ist größer oder gleich , wenn es eine quadratische Untermatrix
, wenn es eine quadratische Untermatrix 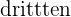 Ranges gibt, deren Determinante nicht Null ist.
Ranges gibt, deren Determinante nicht Null ist.

Da alle Determinanten der Untermatrizen Null sind, ist ihr Rang kleiner als , folglich ist der Rang
, folglich ist der Rang 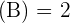 .
.
Mit KI zusammenfassen:













