Faktoren aus einer Wurzel ziehen
Um Faktoren aus einer Wurzel zu ziehen, wird der Radikand in Faktoren zerlegt. Wenn:
1 Ein Exponent des Radikanden kleiner ist als der Wurzelexponent, bleibt der entsprechende Faktor unter der Wurzel.
Beispiele:
a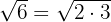 
b 
2Ein Exponent des Radikanden gleich dem Wurzelexponenten ist, steht der entsprechende Faktor außerhalb der Wurzel.
Beispiel:
a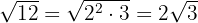 
Wir zerlegen 
in Faktoren, da die 
zur gleichen Potenz wie der Wurzelexponent erhoben wird, können wir die aus dem Radikanden extrahieren
b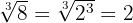 
Wir zerlegen 
in Faktoren, da zur gleichen Potenz wie der Wurzelexponent erhoben wird, können wir aus dem Radikanden extrahieren.
3 Wenn ein Exponent des Radikanden größer als der Wurzelexponent ist, wird der Exponent durch den Wurzelexponenten geteilt. Der erhaltene Quotient ist der Exponent des Faktors außerhalb des Radikanden und der Rest ist der Exponent des Faktors innerhalb des Radikanden.
Beispiele:
a 
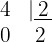
Der Exponent von ist größer als der Wurzelexponent. Daher muss der Exponent 
durch den Wurzelexponenten 
dividiert werden.
Der erhaltene Quotient ist der Exponent des Faktors außerhalb des Radikanden und der Rest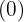 
ist der Exponent des Faktors innerhalb des Radikanden.
b 
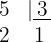
Wir zerlegen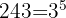 
in Faktoren
Der Exponent ist größer als der Wurzelexponent, also wird der Exponent 
durch den Wurzelexponenten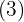 
dividiert.
Der erhaltene Quotient 
ist der Exponent des Faktors außerhalb des Radikanden und der Rest ist der Exponent innerhalb des Radikanden.
Da der Faktor 
gleich 
ist, muss er nicht in den Radikanden eingefügt werden, da er sich nicht ändert, wenn er mit einem anderen Faktor multipliziert wird.
Wenn das Ergebnis der Division des Exponenten eines Faktors durch den Wurzelexponenten einen Rest von 0 ergibt, wird dieser Faktor im Allgemeinen nicht in den Radikanden eingefügt.
c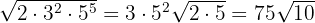 
Es gibt Exponenten im Radikanden, die größer sind als der Wurzelexponent, also werden diese Exponenten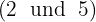 
durch den Wurzelexponenten dividiert.
Jeder der erhaltenen Quotienten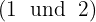 
ist der Exponent des entsprechenden Faktors außerhalb des Radikanden und jeder der erhaltenen Reste 
ist der Exponent der entsprechenden Faktoren innerhalb des Radikanden.
d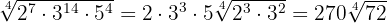 
Die Exponenten des Radikanden sind größer als der Wurzelexponent, also werden diese Exponenten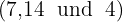 
durch den Wurzelexponenten dividiert.
Jeder der erhaltenen Quotienten (1, 3 und 1) ist der Exponent des entsprechenden Faktors außerhalb des Radikanden und jeder der erhaltenen Reste (3, 2 und 0) ist der Exponent der entsprechenden Faktoren innerhalb des Radikanden.
Faktoren unter eine Wurzel bringen
1 Um Faktoren unter eine Wurzel zu bringen, werden die Faktoren auf den Wurzelexponenten der Wurzel erhöht.
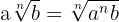
Beispiel:
a
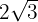
Da der Wurzelexponent ist, wird der Faktor aus der Wurzel quadriert und wir führen die folgenden Operationen durch
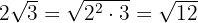
b
Sowohl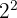 
als auch 
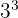werden auf den Wurzelexponenten erhöht unter die Wurzel gebracht
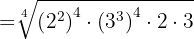
Wir entfernen die Klammern, indem wir die Exponenten multiplizieren
Wir multiplizieren die Potenzen mit gleicher Basis
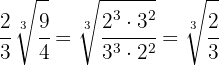
c
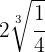
d
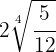
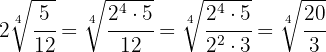
e
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
Im Rahmen einer Internetrecherche zu mathematischen Themen bin ich zufällig auf diese Seite gestoßen.Hier fielen mir Unstimmigkeiten auf: bei den ersten vier Beispielen liegen offensichtlich Formatierungsfehler vor, die sehen nämlich so aus:
„5-3∈ℕ3-5∉ℕ“, „6÷2∈ℕ2÷6∉ℕ“ „6÷2∈ℤ2÷6∉ℤ“ und „(-2)³=-8∈ℤ(-2)⁻³=-⅛∉ℤ“
das kann niemand lesen. Vermutlich fehlt jeweils ein Zeilenvorschub. Oder man schreibt was dazwischen, z.B. ein „aber“:
„5-3∈ℕ aber: 3-5∉ℕ“, „6÷2∈ℕ aber: 2÷6∉ℕ“ „6÷2∈ℤ aber: 2÷6∉ℤ“ und „(-2)³=-8∈ℤ aber: (-2)⁻³=-⅛∉ℤ“
So wäre es verständlich.
Jetzt aber zur Hauptsache: eigentlich ist alles ordentlich und korrekt erklärt. Nur, bei „rationale Zahlen“ steht da:
„““Rationale Zahlen
Eine rationale Zahl ist jede Zahl, die sich als Quotient zweier ganzer Zahlen … darstellen lässt.“““
völlig korrekt, aber im Abschnitt danach:
„““Irrationale Zahlen
Eine Zahl ist irrational, wenn sie unendlich viele nichtperiodische Nachkommastellen …“““
Das passt nicht zusammen, und der Sinn des Begriffs „irrationale Zahl“ bleibt unverständlich. Ja, im formallogischen Sinn kann man sagen „Eine Zahl ist irrational, wenn sie unendlich viele nichtperiodische Nachkommastellen hat und daher nicht als Bruch ausgedrückt werden kann“ – nur wirkt das wie „von hinten durch die Brust ins Auge“. Ich empfehle doch sehr, diesen Satz zu ändern in „Eine irrationale Zahl ist eine Zahl, die sich nicht als Quotient zweier ganzer Zahlen darstellen lässt. Ihre Dezimaldarstellung hat daher unendlich viele nichtperiodische Nachkommastellen“ Dann harmoniert das auch mit dem Abschnitt davor:
Rationale Zahlen – Eine rationale Zahl ist eine Zahl, die sich als Quotient zweier ganzer Zahlen … darstellen lässt.
Irrationale Zahlen – Eine rationale Zahl ist eine Zahl, die sich als Quotient zweier ganzer Zahlen darstellen lässt.
Vielen Dank für die Hinweise. Wir haben die Vorschläge gerne angenommen und im Artikel aktualisiert.