Addition von reellen Zahlen
1 Intern:
Das Erebnis der Addition von zwei natürlichen Zahlen ist eine weitere natürliche Zahl.
Das heißt, wenn a und b zu den reellen Zahlen gehören, wird dies in der mathematischen Sprache wie folgt ausgedrückt:
Dann ist die Summe ebenfalls eine reelle Zahl.
Beispiel:
2 Assoziativ:
Die Art und Weise, wie die Summanden angeordnet sind, ändert nichts am Ergebnis.
Das heißt,
Beispiel:
3 Kommutativ:
Die Reihenfolge der Summanden ändert das Ergebnis nicht.
Beispiel:
4 Neutrales Element:
Das neutrale Element 
ist eine Zahl, die Folgendes erfüllt:
für eine beliebige Zahl 
.
Im Fall der reellen Zahlen ist die 
das neutrale Element der Summe, da jede Zahl, zu der sie addiert wird, die gleiche Zahl ergibt.
Beispiel:
5 Gegenelement:
Zwei Zahlen sind gegensätzlich, wenn ihre Addition das neutrale Element, in diesem Fall die Null, ergibt.
Die Gegenzahl einer Zahl wird als 
angegeben. Somit
Die Gegenzahl der Gegenzahl einer Zahl ist gleich der gleichen Zahl.
Subtraktion von reellen Zahlen
Die Differenz von zwei reellen Zahlen wird als Summe aus Minuend plus der Gegenzahl des Subtrahenden definiert.
Produkt aus reellen Zahlen
Regeln:
1 Intern:
Das Ergebnis der Multiplikation zweier reeller Zahlen ist eine weitere reelle Zahl.
2 Assoziativ:
Die Art und Weise, wie die Faktoren angeordnet sind, ändert nichts am Ergebnis. Wenn , 
und 
reelle Zahlen sind, gilt:
Beispiel:
3 Kommutativ:
Die Reihenfolge der Faktoren hat keinen Einfluss auf das Produkt.
Beispiel:
4 Neutrales Element:
Die 1 ist das neutrale Element der Multiplikation, denn jede Zahl, die mit ihr multipliziert wird, ergibt die gleiche Zahl.
Beispiel:
5 Gegenelement:
Eine Zahl ist der Kehrwert der anderen, wenn ihre Multiplikation das Einheitselement ergibt.
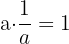
Beispiel:
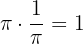
6 Distributiv:
Das Produkt aus einer Zahl und einer Summe ist gleich der Summe der Produkte aus dieser Zahl und den einzelnen Summanden.
7 Gemeinsamen Faktor ausklammern:
Dies ist die Umkehrung des Distributivgesetzes.
Wenn mehrere Summanden einen gemeinsamen Faktor haben, können wir die Summe in ein Produkt umwandeln, indem wir diesen Faktor extrahieren.
Beispiel:
Vorzeichenregel
Die Vorzeichenregel für das Produkt aus ganzen und rationalen Zahlen gilt auch für reelle Zahlen.
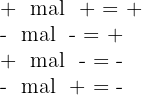
Beispiele:
Division natürlicher Zahlen
Die Division zweier reeller Zahlen ist definiert als das Produkt aus dem Dividenden und dem Kehrwert des Divisors.
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
Im Rahmen einer Internetrecherche zu mathematischen Themen bin ich zufällig auf diese Seite gestoßen.Hier fielen mir Unstimmigkeiten auf: bei den ersten vier Beispielen liegen offensichtlich Formatierungsfehler vor, die sehen nämlich so aus:
„5-3∈ℕ3-5∉ℕ“, „6÷2∈ℕ2÷6∉ℕ“ „6÷2∈ℤ2÷6∉ℤ“ und „(-2)³=-8∈ℤ(-2)⁻³=-⅛∉ℤ“
das kann niemand lesen. Vermutlich fehlt jeweils ein Zeilenvorschub. Oder man schreibt was dazwischen, z.B. ein „aber“:
„5-3∈ℕ aber: 3-5∉ℕ“, „6÷2∈ℕ aber: 2÷6∉ℕ“ „6÷2∈ℤ aber: 2÷6∉ℤ“ und „(-2)³=-8∈ℤ aber: (-2)⁻³=-⅛∉ℤ“
So wäre es verständlich.
Jetzt aber zur Hauptsache: eigentlich ist alles ordentlich und korrekt erklärt. Nur, bei „rationale Zahlen“ steht da:
„““Rationale Zahlen
Eine rationale Zahl ist jede Zahl, die sich als Quotient zweier ganzer Zahlen … darstellen lässt.“““
völlig korrekt, aber im Abschnitt danach:
„““Irrationale Zahlen
Eine Zahl ist irrational, wenn sie unendlich viele nichtperiodische Nachkommastellen …“““
Das passt nicht zusammen, und der Sinn des Begriffs „irrationale Zahl“ bleibt unverständlich. Ja, im formallogischen Sinn kann man sagen „Eine Zahl ist irrational, wenn sie unendlich viele nichtperiodische Nachkommastellen hat und daher nicht als Bruch ausgedrückt werden kann“ – nur wirkt das wie „von hinten durch die Brust ins Auge“. Ich empfehle doch sehr, diesen Satz zu ändern in „Eine irrationale Zahl ist eine Zahl, die sich nicht als Quotient zweier ganzer Zahlen darstellen lässt. Ihre Dezimaldarstellung hat daher unendlich viele nichtperiodische Nachkommastellen“ Dann harmoniert das auch mit dem Abschnitt davor:
Rationale Zahlen – Eine rationale Zahl ist eine Zahl, die sich als Quotient zweier ganzer Zahlen … darstellen lässt.
Irrationale Zahlen – Eine rationale Zahl ist eine Zahl, die sich als Quotient zweier ganzer Zahlen darstellen lässt.
Vielen Dank für die Hinweise. Wir haben die Vorschläge gerne angenommen und im Artikel aktualisiert.