Überblick über das Integral des Sinus
Wir erinnern uns daran, dass die Ableitung der Funktion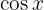 
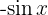ist. Dies sagt uns direkt, dass die Ableitung von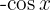 
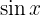ist. Nun wird das unbestimmte Integral als die Umkehrung der Integration betrachtet, daher folgt, dass das Integral von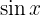 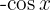sein muss.Wir müssen jedoch bedenken, dass die Ableitung einer beliebigen Konstanten 0ist, sodass auch die Ableitung von 
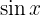ist. Somit ist die Stammfunktion oder das Integral von 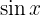tatsächlich . In anderen Worten
Außerdem müsssen wir die Kettenregel beachten, aus der folgt, dass die Ableitung von 
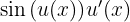ist. Daraus folgt auch, dass
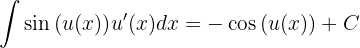
Aufgaben zur Integration der Sinusfunktion
Für diese Übungen gehen wir davon aus, dass du die grundlegenden Eigenschaften von Integralen kennst und weißt, wie man Integrale durch Substitution, partielle Integration usw. löst. Falls du dich nicht mehr an diese Methoden erinnerst, schau dir doch unsere Artikel an, in denen wir sie erklären.
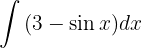
Wir integrieren direkt
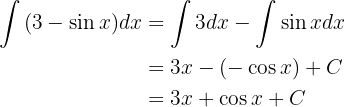
Wir integrieren mit der Methode der Substitution.
Wir nehmen
Wir setzen in das Integral ein und erhalten
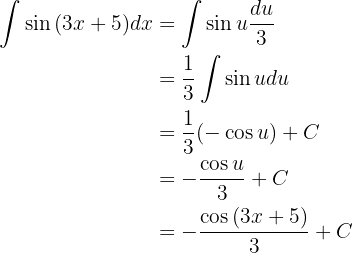
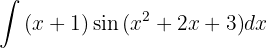
Wir integrieren diese Funktion mit der Substitution.
Wir nehmen
Wir multiplizieren und dividieren unser Integral mit und durch 
um seinen Wert nicht zu verändern, substituieren und lösen
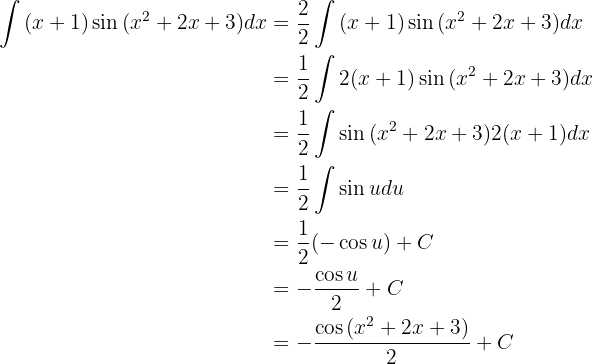
Wir integrieren diese Funktion partiell.
Dabei beachten wir
Wir überlegen uns, welcher Teil der Funktion 
sein wird und welcher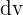 
sein wird. In diesem Fall gehen wir wie folgt vor
und
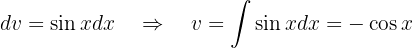
Wir setzen diese Werte in eine Formel der partiellen Integration ein und erhalten
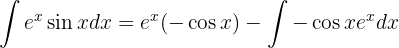
Wir wenden erneut die partielle Integration an
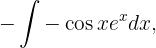
in diesem Fall sind 
und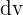
und
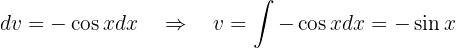
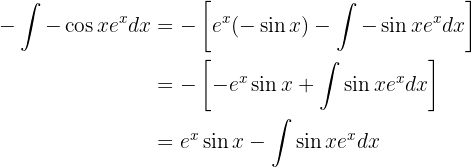
Wenn wir all dies in das erste Integral einsetzen, erhalten wir das Integral, das wir berechnen möchten, auf der linken und rechten Seite, jedoch mit negativem Vorzeichen. Daher müssen wir nur noch das Integral, das wir ermitteln möchten, bestimmen
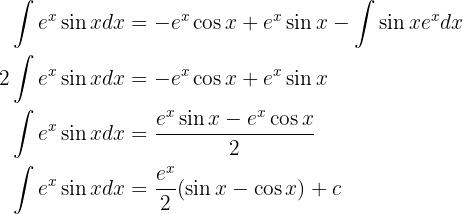
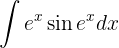
Wir integrieren durch Substitution.
Wir nehmen
und
setzen diese Werte in eine Formel der partiellen Integration ein. Wir erhalten
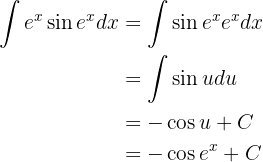
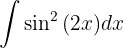
Um diese Funktion zu integrieren, müssen wir sie zunächst vereinfachen. Dazu halten wir uns die folgende trigonometrische Identität vor Augen
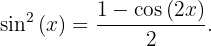
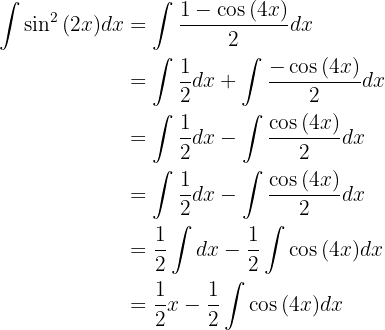
Um das Integral
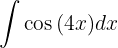zu lösen,
substituieren wir. Wir nehmen
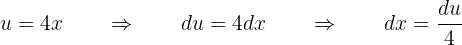
Und somit
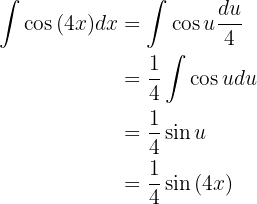
Wir setzen in das vorherige Integral ein und erhalten
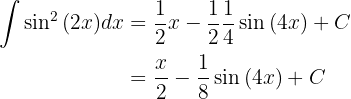
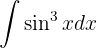
Zunächst schreiben wir unser Integral in einer angenehmeren Form auf
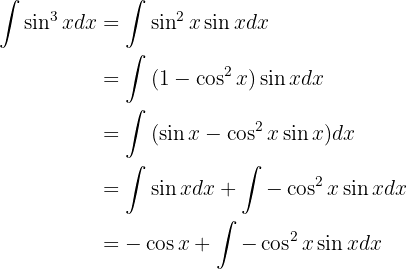
Nun müssen wir nur noch integrieren
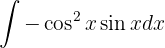
Wir integrieren durch Substitution. Wir nehmen
Und somit
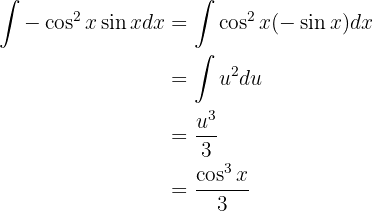
Wir setzen in das ursprüngliche Integral ein
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
