Willkommen zu unserem Kapitel über das Lösen von Problemen mit der Methode der Integration durch Substitution. Dieser Ansatz, der auch als Variablentausch bezeichnet wird, ist ein wichtiges Werkzeug in der Welt der Integralrechnung, mit dem du eine Vielfalt von Funktionen effizient bewältigen kannst.
Wir leiten dich durch gelöste Aufgaben, die dir zeigen, wie du eine geeignete Substitution auswählst, um komplexere Ausdrücke zu vereinfachen. Jedes Beispiel enthält eine schrittweise Beschreibung der angewandten Strategie, von der Auswahl der Substitution über die Anwendung der Kettenregel bis hin zur abschließenden Auswertung.
Die Methode der Integration durch Substitution ist für die Bewältigung anspruchsvoller Integrale unerlässlich, und ihre Beherrschung öffnet dir die Tür zur effizienten Lösung einer Vielzahl von mathematischen Problemen. Begleite uns auf dieser lehrreichen Reise, auf der wir die Eleganz und Nützlichkeit der Integration durch Substitution erforschen und auf der du die notwendigen Fähigkeiten entwickelst, um Integrationsprobleme selbstbewusst anzugehen.

1 Wir führen die Substitution durch und berechnen das Differential
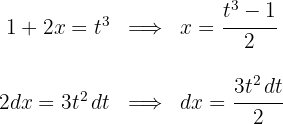
2 Wir setzen in das Integral ein und vereinfachen
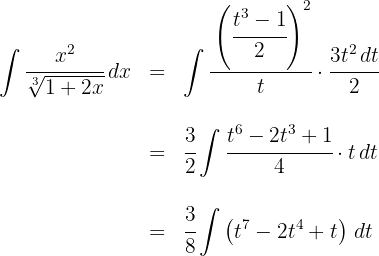
3 Wir lösen das erhaltene Integral
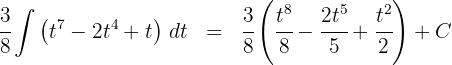
4 Wir kehren wie folgt zur Ausgangsvariablen zurück: 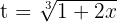

Die Lösung in Bezug auf die Ausgangsvariable lautet also
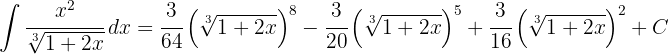
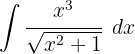
1 Wir führen die Substitution durch und berechnen das Differential
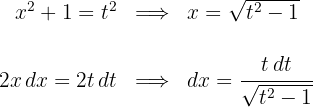
2 Wir setzen in das Integral ein und vereinfachen

3 Wir lösen das erhaltene Integral
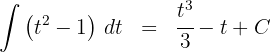
4 Wir kehren wie folgt zur Ausgangsvariablen zurück: 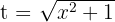
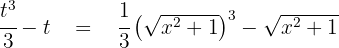
Die Lösung in Bezug auf die Ausgangsvariable lautet also


1 Wir führen die Substitution durch und berechnen das Differential
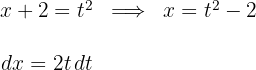
2 Wir setzen in das Integral ein und vereinfachen
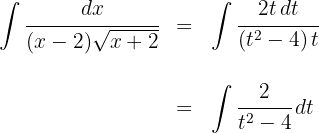
3 Wir lösen das erhaltene Integral
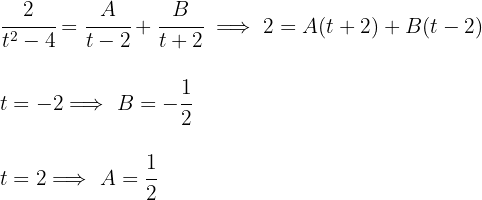
Das Integral ist

4 Wir kehren wie folgt zur Ausgangsvariablen zurück: 
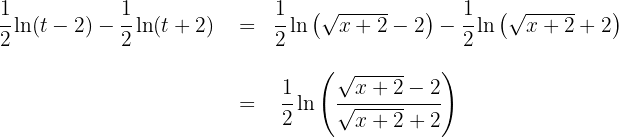
Die Lösung in Bezug auf die Ausgangsvariable lautet also

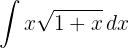
1 Wir führen die Substitution durch und berechnen das Differential

2 Wir setzen in das Integral ein und vereinfachen
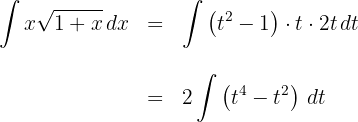
3 Wir lösen das erhaltene Integral
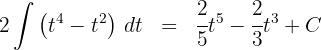
4 Wir kehren wie folgt zur Ausgangsvariablen zurück: 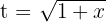
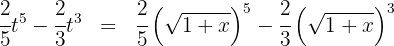
Die Lösung in Bezug auf die Ausgangsvariable lautet also
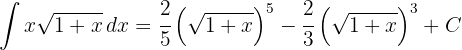
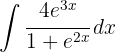
1 Wir führen die Substitution durch und berechnen das Differential

2 Wir setzen in das Integral ein und vereinfachen
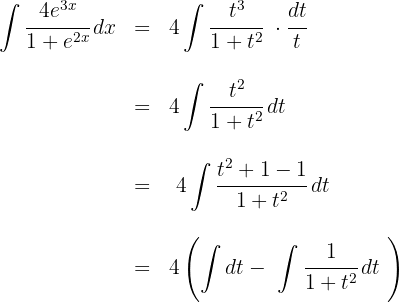
3 Wir lösen das erhaltene Integral
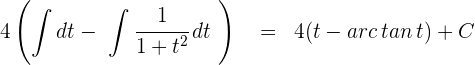
4 Wir kehren wie folgt zur Ausgangsvariablen zurück: 
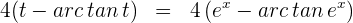
Die Lösung in Bezug auf die Ausgangsvariable lautet also
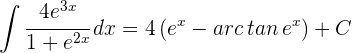

1 Wir führen die Substitution durch und berechnen das Differential
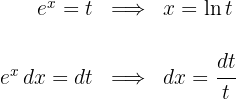
2 Wir setzen in das Integral ein und vereinfachen

3 Wir lösen das erhaltene Integral
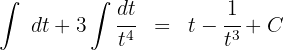
4 Wir kehren wie folgt zur Ausgangsvariablen zurück: 

Die Lösung in Bezug auf die Ausgangsvariable lautet also
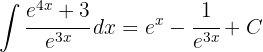
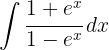
1 Wir führen die Substitution durch und berechnen das Differential
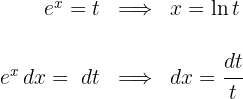
2 Wir setzen in das Integral ein und vereinfachen
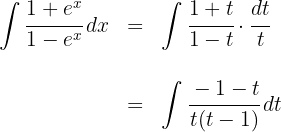
3 Wir lösen das erhaltene Integral
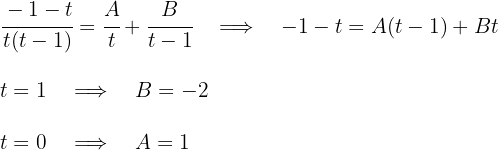
Das Integral ist
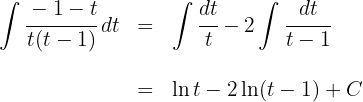
4 Wir kehren wie folgt zur Ausgangsvariablen zurück: 
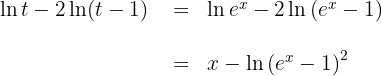
Die Lösung in Bezug auf die Ausgangsvariable lautet also


1 Wir führen die Substitution durch und berechnen das Differential


2 Wir setzen in das Integral ein und vereinfachen mithilfe der trigonometrischen Identitäten

3 Wir lösen die erhaltenen Integrale

4 Wir kehren zur Ausgangsvariablen zurück. Hierfür bestimmen wir das  der ursprünglichen Substitution
der ursprünglichen Substitution

Wir berechnen für den Sinus und Kosinus von 


Das Ergebnis wird also in der Variablen  ausgedrückt als
ausgedrückt als
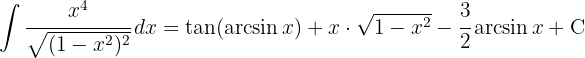

1 Wir führen die Substitution durch und berechnen das Differential

2 Wir setzen in das Integral ein und vereinfachen
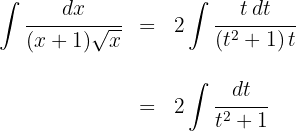
3 Wir lösen das erhaltene Integral
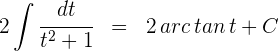
4 Wir kehren wie folgt zur Ausgangsvariablen zurück: 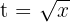
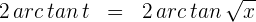
Die Lösung in Bezug auf die Anfangsvariable lautet also
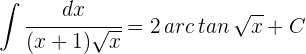

1 Wir führen die Substitution durch und berechnen das Differential
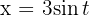
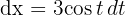
2 Wir setzen in das Integral ein und vereinfachen mithilfe der trigonometrischen Identitäten

3 Wir lösen die erhaltenen Integrale
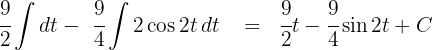
4 Wir kehren wie folgt zur Anfangsvariablen zurück. Hierfür bestimmen wir das  der ursprünglichen Substitution
der ursprünglichen Substitution

Wir berechnen den Sinus und Kosinus von 
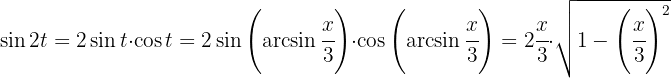
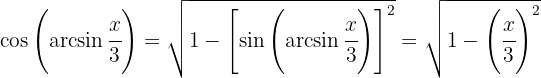
Das Ergebnis wird also in der Variablen  ausgedrückt als
ausgedrückt als
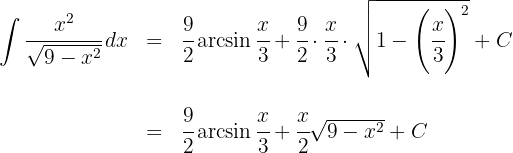

1 Wir führen die Substitution durch und berechnen das Differential


2 Wir setzen in das Integral ein und vereinfachen
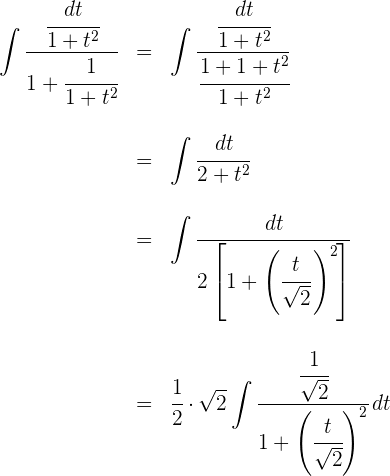
3 Wir lösen die erhaltenen Integrale

4 Wir kehren zur Ausgangsvariablen zurück
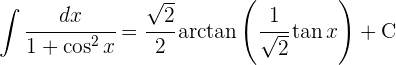
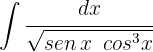
1 Wir führen die Substitution durch und berechnen das Differential
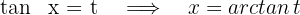

2 Wir setzen in das Integral ein und vereinfachen
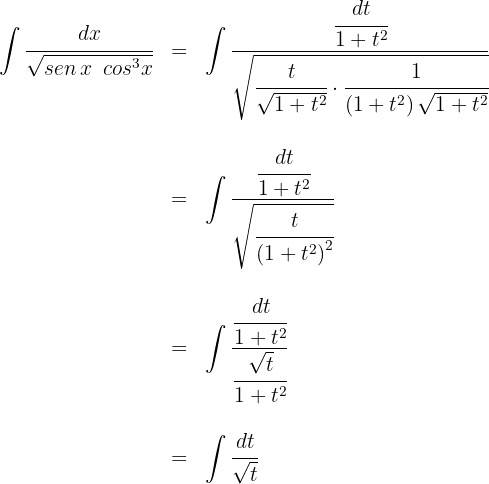
3 Wir lösen die erhaltenen Integrale

4 Wir kehren zur Ausgangsvariablen zurück
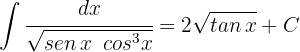

1 Wir führen die Substitution durch und berechnen das Differential


2 Wir setzen in das Integral ein und vereinfachen

3 Wir lösen die erhaltenen Integrale

4 Wir kehren zur Ausgangsvariablen zurück


1 Wir führen die Substitution durch und berechnen das Differential

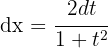
2 Wir setzen in das Integral ein und vereinfachen
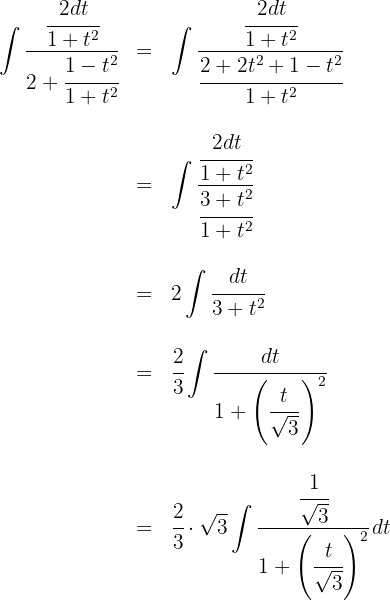
3 Wir lösen die erhaltenen Integrale

4 Wir kehren zur Ausgangsvariablen zurück

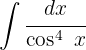
1 Wir führen die Substitution durch und berechnen das Differential
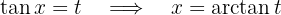

2 Wir setzen in das Integral ein und vereinfachen

3 Wir lösen die erhaltenen Integrale
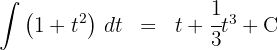
4 Wir kehren zur Ausgangsvariablen zurück
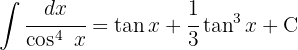
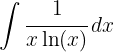
1 Wir führen die Substitution durch und berechnen das Differential
Wir führen die Substitution durch und berechnen das Differential
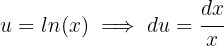
2 Wir setzen in das Integral ein und vereinfachen
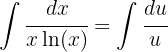
3 Wir lösen das erhaltene Integral
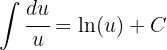
4 Wir kehren zur Ausgangsvariablen zurück

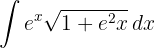
1 Wir führen die Substitution durch und berechnen das Differential
Wir führen die Substitution durch und berechnen das Differential
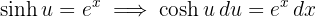
2 Wir setzen in das Integral ein und vereinfachen
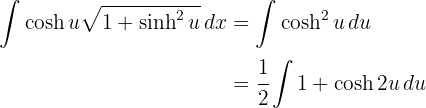
3 Wir lösen das erhaltene Integral
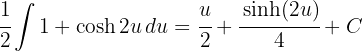
4 Wir kehren zur Ausgangsvariablen zurück


1 Wir führen die Substitution durch und berechnen das Differential
Wir führen die Substitution durch und berechnen das Differential
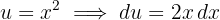
2 Wir setzen in das Integral ein und vereinfachen
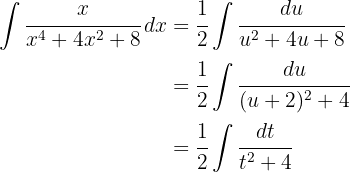
3 Wir lösen das erhaltene Integral
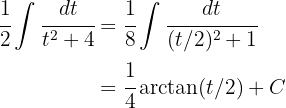
4 Wir kehren wie folgt zur Ausgangsvariablen zurück: 

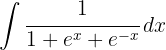
1 Wir führen die Substitution durch und berechnen das Differential
Wir führen die Substitution durch und berechnen das Differential
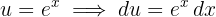
2 Wir setzen in das Integral ein und vereinfachen
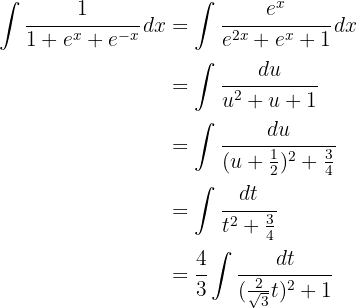
3 Wir lösen das erhaltene Integral
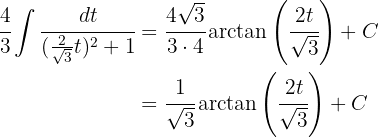
4 Wir kehren wie folgt zur Ausgangsvariablen zurück: 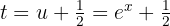
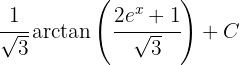

1 Wir führen die Substitution durch und berechnen das Differential
Wir führen die Substitution durch und berechnen das Differential
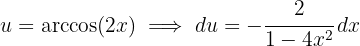
2 Wir setzen in das Integral ein und vereinfachen
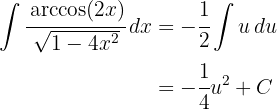
3 Wir kehren wie folgt zur Ausgangsvariablen zurück: 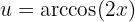
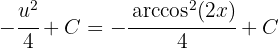
Mit KI zusammenfassen:



