
Grundregeln zum Rechnen mit Determinanten
Determinanten spielen bei der Berechnung von Matrizen eine wichtige Rolle, denn im Gegensatz zu Matrizen kann man aktiv mit ihnen rechnen.
Je nach Rang der Determinante eignen sich andere Vorgehensweisen für die Berechnung.
Während 2x2- und 3x3-Determinanten nach Formeln berechnet werden können, dient zur Berechnung von Determinanten höheren Ranges z.B. das Gauß-Verfahren.
Welche generellen Eigenschaften beim Rechnen mit Determinanten außerdem zu beachten sind, haben wir im Folgenden zusammengefasst:
Eigenschaften im Überblick
1 Die Determinante einer Matrix  ist gleich der Determinante ihrer Transponierten
ist gleich der Determinante ihrer Transponierten 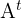 .
.


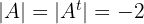
2  Wenn:
Wenn:
sie zwei gleiche Zeilen (bzw. Spalten) besitzt.

alle Elemente einer Zeile (oder Spalte) gleich Null sind.

die Elemente einer Zeile (oder Spalte) die Linearkombination anderer sind.

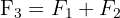
3 Eine Dreiecksdeterminante ist gleich dem Produkt der Elemente ihrer Hauptdiagonalen.

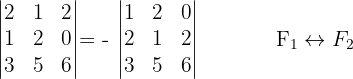
4 Wenn zwei Zeilen (oder Spalten) einer Determinante gegeneinander ausgetauscht werden, verändert sich nur das Vorzeichen des Werts.
5 Wenn zu den Elementen einer Zeile (oder Spalte) die Elemente einer anderen addiert werden, die zuvor mit einer reellen Zahl multipliziert wurden, verändert sich der Wert der Determinante nicht. .
Das heißt, wenn eine Zeile (oder Spalte) als Linearkombination der anderen dargestellt werden kann, verändert sich der Wert der Determinante nicht.

6 Wenn eine Determinante mit einer reellen Zahl multipliziert wird, wirkt sich die Multiplikation auf eine beliebige Zeile (oder Spalte) aus; jedoch immer nur auf eine.

7 Wenn alle Elemente einer Zeile (oder Spalte) aus zwei Summanden bestehen, kann die Determinante in die Summe aus zwei Determinanten zerlegt werden, in denen die übrigen Zeilen (oder Spalten) unverändert bleiben.

8 
Die Determinante eines Produkts ist gleich dem Produkt der Determinanten.
Mit KI zusammenfassen:













