Willkommen zur zweiten Ausgabe unserer Rubrik, die sich mit dem Lösen von Aufgaben zu Flächen und Volumen beschäftigt. In diesem zweiten Eintrag erkunden wir die aufregende Welt der geometrischen Abmessungen noch weiter und konzentrieren uns auf die Bestimmung von Flächeninhalten und Volumen von Körpern.
In diesem Leitfaden stellen wir dir gelöste Probleme vor, die ein breites Spektrum an dreidimensionalen und zweidimensionalen Figuren abdecken. Jedes Beispiel enthält eine schrittweise Beschreibung der angewandten Strategie, von der Anwendung spezifischer Formeln bis zur Berücksichtigung von Sonderfällen, die jedes Problem einzigartig machen.
Darüber hinaus werden wir uns mit der Lösung schwierigerer Probleme befassen, die die Kombination von Flächen und Volumina beinhalten, und dir die Werkzeuge an die Hand geben, die du brauchst, um mit komplexen geometrischen Situationen umzugehen.
Berechne die Fläche und das Volumen eines Tetraeders mit einer Kantenlänge von 5 cm.
Berechne die Fläche und das Volumen eines Tetraeders mit einer Kantenlänge von 5 cm.
1 Um die Gesamtfläche eines Tetraeders zu berechnen, verwenden wir 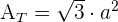
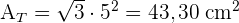
2 Um Volumen eines Tetraeders zu berechnen, verwenden wir 
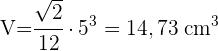
Berechne die Diagonale, die Seitenfläche, die Gesamtfläche und das Volumen eines Würfels mit einer Kantenlänge von 5 cm.
Berechne die Diagonale, die Seitenfläche, die Gesamtfläche und das Volumen eines Würfels mit einer Kantenlänge von 5 cm
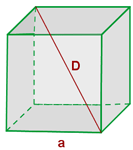
1 Um die Diagonale zu berechnen, verwenden wir 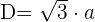
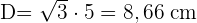
2 Um die Seitenfläche zu berechnen, verwenden wir 
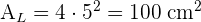
3 Um die Gesamtfläche zu berechnen, verwenden wir 
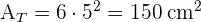
4 Um das Volumen zu berechnen, verwenden wir 
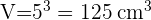
Berechne die Fläche und das Volumen eines Oktaeders mit einer Kantenlänge von 5 cm.
Berechne die Fläche und das Volumen eines Oktaeders mit einer Kantenlänge von 5 cm.
1 Um die Gesamtfläche eines Oktaeders zu berechnen, verwenden wir 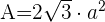
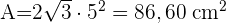
2 Um das Volumen eines Oktaeders zu berechnen, verwenden wir 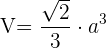
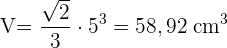
Berechne die Fläche und das Volumen eines Dodekaeders mit einer Kantenlänge von 10 cm, wenn du weißt, dass das Apothema einer seiner Seiten 6,88 cm misst.
Berechne die Fläche und das Volumen eines Dodekaeders mit einer Kantenlänge von 10 cm, wenn du weißt, dass das Apothema einer seiner Seiten 6,88 cm misst.
1 Um die Gesamtfläche eines Dodekaeders zu berechnen, verwenden wir 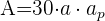
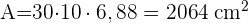
2 Um das Volumen eines Dodekaeders zu berechnen, verwenden wir 
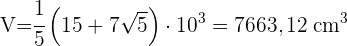
Berechne die Fläche und das Volumen eines Ikosaeders mit einer Kantenlänge von 5 cm.
Berechne die Fläche und das Volumen eines Ikosaeders mit einer Kantenlänge von 5 cm.
1 Um die Gesamtfläche eines Ikosaeders zu berechnen, verwenden wir 
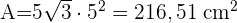
2 Um das Volumen eines Ikosaeders zu berechnen, verwenden wir 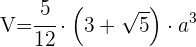
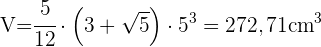
Berechne die Seitenfläche, die Gesamtfläche und das Volumen eines Prismas, dessen Grundfläche ein Rhombus mit den Diagonalen 12 und 18 cm ist.
Berechne die Seitenfläche, die Gesamtfläche und das Volumen eines Prismas, dessen Grundfläche ein Rhombus mit den Diagonalen 12 und 18 cm ist.
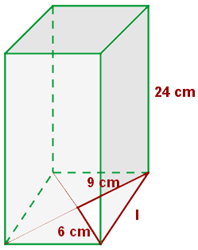
1 Wenn man die Diagonalen auf der Grundfläche zeichnet, werden rechtwinklige Dreiecke gebildet, so dass man die Maße der Kanten der Grundfläche berechnen kann

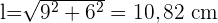
2 Die Seitenfläche ist die Fläche der 4 seitlichen Vierecke
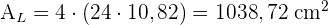
3 Die Gesamtfläche ist die Summe aus der Seitenfläche und den Flächeninhalten der Grundflächen
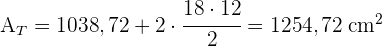
4 Das Volumen ist gleich der Fläche der Grundfläche multipliziert mit der Höhe
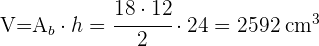
Berechne die Seitenfläche, die Gesamtfläche und das Volumen einer viereckigen Pyramide mit einer Kantenlänge von 10 cm und einer Höhe von 12 cm.
Berechne die Seitenfläche, die Gesamtfläche und das Volumen einer viereckigen Pyramide mit einer Kantenlänge von 10 cm und einer Höhe von 12 cm.
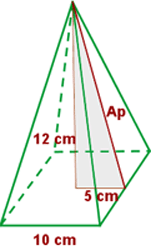
1 Wir berechnen die Höhe  eines der seitlichen Dreiecke
eines der seitlichen Dreiecke
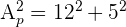
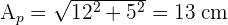
2 Die Seitenfläche ist die Fläche der 4 seitlichen Dreiecke
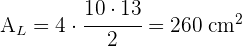
3 Die Gesamtfläche ergibt sich aus der Summe der Seitenfläche und dem Flächeninhalt der Grundfläche

4 Das Volumen einer Pyramide wird wie folgt berechnet: 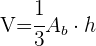
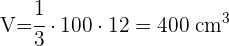
Berechne die Seitenfläche, die Gesamtfläche und das Volumen einer sechseckigen Pyramide mit einer Grundkantenlänge von 16 cm und einer Seitenkantenlänge von 28 cm.
Berechne die Seitenfläche, die Gesamtfläche und das Volumen einer sechseckigen Pyramide mit einer Grundkantenlänge von 16 cm und einer Seitenkantenlänge von 28 cm.
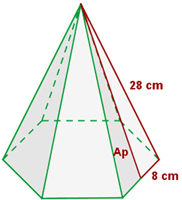
1 Wir berechnen die Höhe  eines der seitlichen Dreiecke
eines der seitlichen Dreiecke
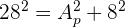
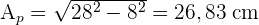
2 Die Seitenfläche ist die Fläche der 6 seitlichen Dreiecke
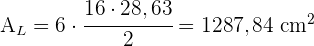
3 Die Gesamtfläche ist die Summe der Seitenflächen und der Grundfläche. Wir müssen also die Grundfläche des Sechsecks berechnen und dann in die Formel für die Fläche des Sechsecks einsetzen
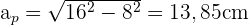
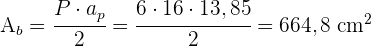
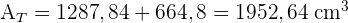
4 Das Volumen einer Pyramide wird wie folgt berechnet: 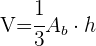 . Wir müssen zunächst die Höhe der Pyramide berechnen:
. Wir müssen zunächst die Höhe der Pyramide berechnen:
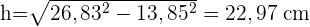
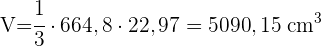
Berechne die Seitenfläche, die Gesamtfläche und das Volumen einer viereckigen Pyramide mit den Grundkanten 24 und 14 cm und der Seitenkante 13 cm.
Berechne die Seitenfläche, die Gesamtfläche und das Volumen einer viereckigen Pyramide mit den Grundkanten 24 und 14 cm und der Seitenkante 13 cm.
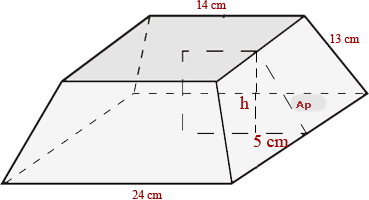
1 Das Apothema fällt mit der Höhe des seitlichen Trapezes zusammen:

2 Die Höhe des Pyramidenstumpfes wird mithilfe des Satzes des Pythagoras berechnet:
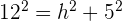
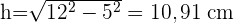
3 Wir berechnen den Umfang P der größeren Grundfläche und den Umfang P' der kleineren Grundfläche:
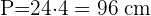

4 Die seitliche Fläche ergibt sich aus 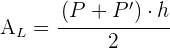 , was der Summe der Flächen der 4 seitlichen Trapeze entspricht
, was der Summe der Flächen der 4 seitlichen Trapeze entspricht
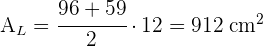
5 Wir berechnen die Fläche A der größeren Grundfläche und die Fläche A' der kleineren Grundfläche und addieren sie zusammen mit der Seitenfläche, um die Gesamtfläche zu erhalten

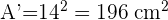

6 Das Volumen wird mit 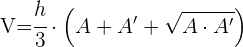 berechnet
berechnet
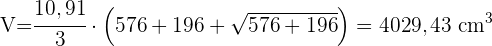
Berechne die Seitenfläche, die Gesamtfläche und das Volumen eines Kegels, dessen Mantellinie 13 cm und der Radius der Grundfläche 5 cm beträgt.
Berechne die Seitenfläche, die Gesamtfläche und das Volumen eines Kegels, dessen Mantellinie 13 cm und der Radius der Grundfläche 5 cm beträgt.
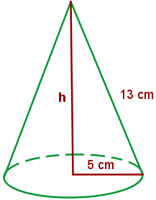
1 Die Seitenfläche wird mit  berechnet
berechnet
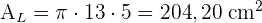
2 Die Gesamtfläche wird berechnet, indem die Fläche der Seite und die Fläche der Grundfläche addiert werden
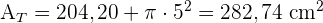
3 Das Volumen wird mit 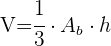 und die Höhe mit dem Satz des Pythagoras berechnet.
und die Höhe mit dem Satz des Pythagoras berechnet.

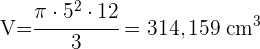
Berechne die Seitenfläche, die Gesamtfläche und das Volumen eines Kegels mit einer Höhe von 4 cm und einem Radius der Grundfläche von 3 cm.
Berechne die Seitenfläche, die Gesamtfläche und das Volumen eines Kegels mit einer Höhe von 4 cm und einem Radius der Grundfläche von 3 cm.
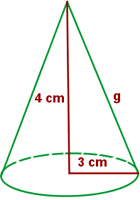
1 Wir berechnen die Mantellinie mit dem Satz des Pythagoras:
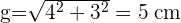
2 Wir berechnen die Seitenfläche
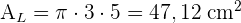
3 Wir berechnen die Gesamtfläche:
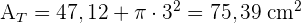
4 Wir berechnen das Volumen
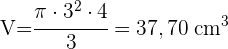
Berechne die Seitenfläche, die Gesamtfläche und das Volumen eines Kegelstumpfes mit den Radien 6 und 2 cm und der Höhe 10 cm.
Berechne die Seitenfläche, die Gesamtfläche und das Volumen eines Kegelstumpfes mit den Radien 6 und 2 cm und der Höhe 10 cm.
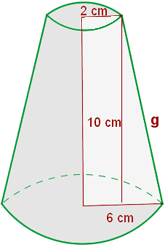
1 Wir berechnen die Mantellinie mit dem Satz des Pythagoras:
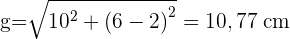
2 Wir berechnen die Seitenfläche
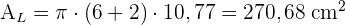
3 Wir berechnen die Gesamtfläche:
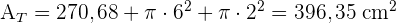
4 Wir berechnen das Volumen
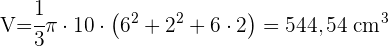
Berechne die Seitenfläche, die Gesamtfläche und das Volumen des Kegelstumpfs mit den Radien 12 und 10 cm und der Mantellinie 15 cm.
Berechne die Seitenfläche, die Gesamtfläche und das Volumen des Kegelstumpfs mit den Radien 12 und 10 cm und der Mantellinie 15 cm.
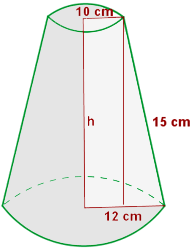
1 Wir berechnen die Höhe mit dem Satz des Pythagoras:
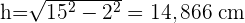
2 Wir berechnen die Seitenfläche
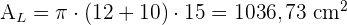
3 Wir berechnen die Gesamtfläche:
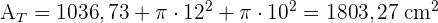
4 Wir berechnen das Volumen
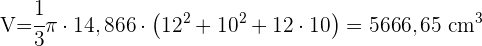
Berechne die Fläche des Kreises, der sich ergibt, wenn man eine Kugel mit dem Radius 35 cm durch eine Ebene schneidet, die 21 cm vom Mittelpunkt der Kugel entfernt ist.
Berechne die Fläche des Kreises, der sich ergibt, wenn man eine Kugel mit dem Radius 35 cm durch eine Ebene schneidet, die 21 cm vom Mittelpunkt der Kugel entfernt ist.
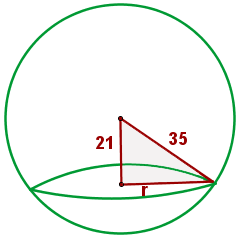
1 Wir berechnen den Radius mit dem Satz des Pythagoras

2 Wir berechnen die Fläche

Berechne die Fläche und das Volumen einer Kugel, die in einen 2 m hohen Zylinder eingeschrieben ist.
Berechne die Fläche und das Volumen einer Kugel, die in einen 2 m hohen Zylinder eingeschrieben ist.
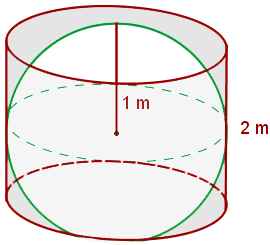
1 Der Radius der Kugel wäre die Hälfte der Höhe des Zylinders, r=1 m, sodass wir zur Berechnung der Fläche übergehen:
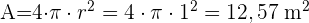
2 Wir berechnen das Volumen:
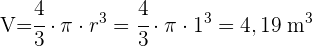
Berechne das Volumen einer Halbkugel mit einem Radius von 10 cm.
Berechne das Volumen einer Halbkugel mit einem Radius von 10 cm.
1 Eine Halbkugel ist die Hälfte einer Kugel, ihr Volumen wäre also gleich:
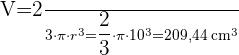
Berechne die Fläche und das Volumen des folgenden Kugelsegments.
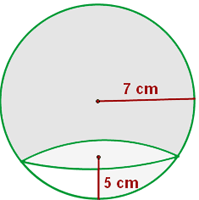
Berechne die Fläche und das Volumen des folgenden Kugelsegments.
1 Die Fläche eines Kugelsegments wird wie folgt berechnet: 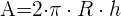
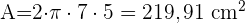
2 Das Volumen eines Kugelsegments wird wie folgt berechnet: 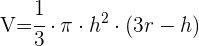
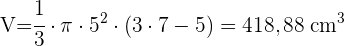
Berechne die Fläche und das Volumen einer Kugelschicht, deren Umfänge einen Radius von 10 cm und 8 cm haben und deren Abstand 6 cm beträgt.
Berechne die Fläche und das Volumen einer Kugelschicht, deren Umfänge einen Radius von 10 cm und 8 cm haben und deren Abstand 6 cm beträgt.
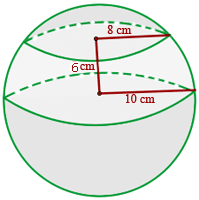
1 Die Fläche einer kugelförmigen Oberfläche wird berechnet mit: 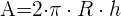
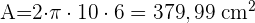
2 Das Volumen einer kugelförmigen Oberfläche wird berechnet mit: 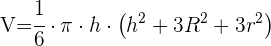
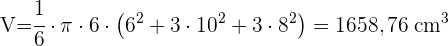
Ein Würfel mit einer Kantenlänge von 20 cm ist mit Wasser gefüllt. Würde dieses Wasser in eine Kugel mit dem Radius 20 cm passen?
Ein Würfel mit einer Kantenlänge von 20 cm ist mit Wasser gefüllt. Würde dieses Wasser in eine Kugel mit dem Radius 20 cm passen?
1 Wir berechnen das Volumen des Würfels und der Kugel und vergleichen die jeweiligen Volumen:
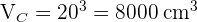
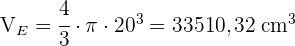
Da das Volumen der Kugel größer ist als das Volumen des Würfels, passt das Wasser in den Würfel.
Die Kuppel einer Kathedrale hat die Form einer Halbkugel und einen Durchmesser von 50 m. Wenn die Restaurierung 300 € pro m2 kostet, wie viel würde die Restaurierung dann insgesamt kosten?
Die Kuppel einer Kathedrale hat die Form einer Halbkugel und einen Durchmesser von 50 m. Wenn die Restaurierung 300 € pro m2 kostet, wie viel würde die Restaurierung dann insgesamt kosten?
1 Wir berechnen die Fläche der Halbkugel
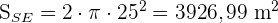
2 Wir multiplizieren die Oberfläche mit den Kosten pro 
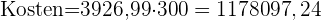
Angenommen, wir haben einen Würfel mit der Seitenlänge 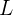 , der mit Wasser gefüllt ist. Wir möchten das Wasser aus dem Würfel in eine Kugel mit einem bestimmten Radius gießen. Welchen Radius muss die Kugel haben, damit das Volumen des Würfels hineinpasst?
, der mit Wasser gefüllt ist. Wir möchten das Wasser aus dem Würfel in eine Kugel mit einem bestimmten Radius gießen. Welchen Radius muss die Kugel haben, damit das Volumen des Würfels hineinpasst?
Das Volumen eines Würfels mit einer Seitenlänge von 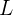 ist
ist 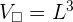 . Dabei
. Dabei  sei der Radius der Kugel. Wir möchten einen Ausdruck für
sei der Radius der Kugel. Wir möchten einen Ausdruck für  in Abhängigkeit von
in Abhängigkeit von 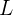 finden. Das Volumen der Kugel ist
finden. Das Volumen der Kugel ist
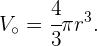
Wir möchten also, dass die folgende Gleichung erfüllt ist.
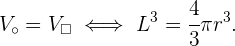
Wir bestimmen  .
.
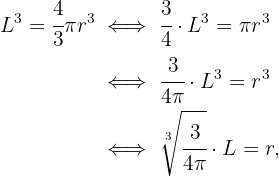 ,
,
wobei 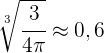 ist.
ist.
Wenn eine Metallkugel mit dem Radius 5 cm ein Gewicht von 2 kg hat, wie viel wiegt dann eine Kugel mit dem Radius 20 cm?
Das Volumen der 5-cm-Kugel ist
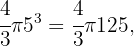 ,
,
während das Volumen einer 20-cm-Kugel
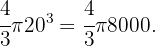 ist
ist
Nun wollen wir sehen, wie oft die Masse der kleinen Kugel in die große Kugel passt:
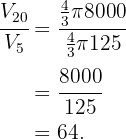
Jede der Kugeln wiegt 2 kg, so dass sie insgesamt  wiegen.
wiegen.
Berechne das Volumen des folgenden trapezförmigen Prismas:
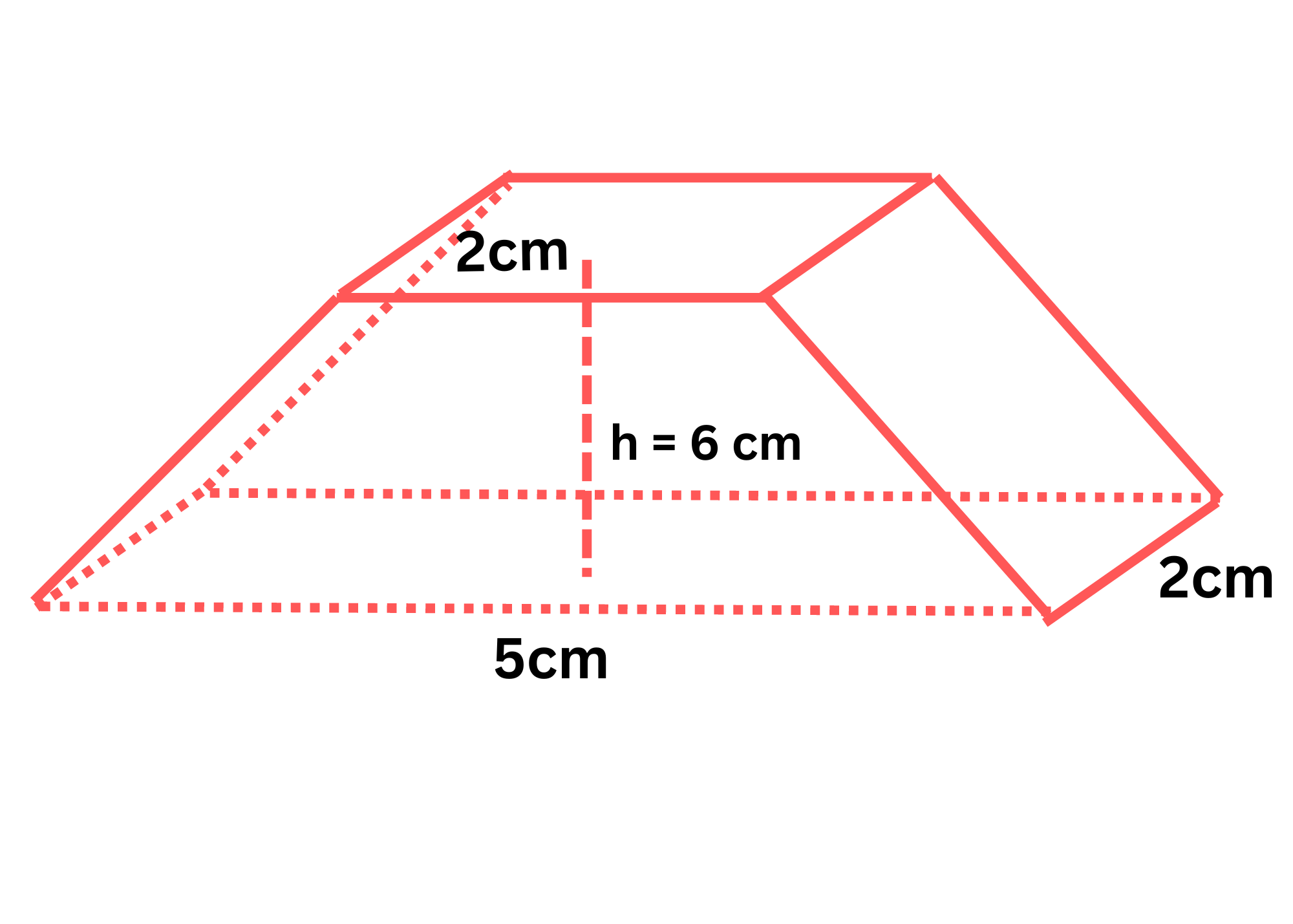
Zunächst sei daran erinnert, dass die Fläche eines Trapezes berechnet werden kann, wenn man die kleinere Grundseite, die größere Grundseite und die Höhe kennt. In diesem Fall beträgt die größere Grundseite 5 cm, die kleinere Grundseite 2 cm und die Höhe 6 cm. Der Flächeninhalt ist also
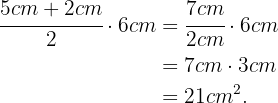
Nun multiplizieren wir einfach diese Fläche mit der Breite, die 2 cm beträgt, um das Volumen zu erhalten:
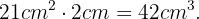
Angenommen, wir haben einen kegelförmigen Becher mit dem Radius  und der Höhe
und der Höhe  , den wir mit Wasser füllen. Wie viele Becher brauchen wir, um ein kugelförmiges Aquarium mit dem Radius
, den wir mit Wasser füllen. Wie viele Becher brauchen wir, um ein kugelförmiges Aquarium mit dem Radius  zu befüllen?
zu befüllen?
Das Volumen eines Kegels ist gleich
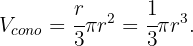
Das Volumen einer Kugel ist
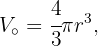 .
.
Also stellen wir fest, dass wir genau 4 Becher brauchen, um das Aquarium zu füllen, da
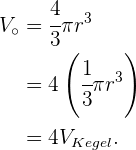
Angenommen, wir haben ein zylinderförmiges Glas mit dem Radius  und der Höhe
und der Höhe  , das wir mit Wasser füllen. Wie viele Gläser brauchen wir, um einen tiefen Teller in Form einer Halbkugel mit dem Radius
, das wir mit Wasser füllen. Wie viele Gläser brauchen wir, um einen tiefen Teller in Form einer Halbkugel mit dem Radius  zu füllen?
zu füllen?
Das Volumen dieses Zylinders ist gleich
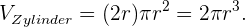
Das Volumen einer Kugel ist
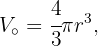 ,
,
aber da wir nur die Hälfte dieses Volumens benötigen:
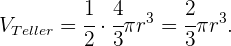 .
.
Wir stellen also fest, dass wir nur ein Drittel (1/3) der Gesamtkapazität des Gefäßes benötigen, da
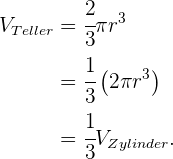
Mit KI zusammenfassen:


