Definition: Inverse Matrix
Das Produkt aus einer Matrix und ihrer Inversen ist die Einheitsmatrix
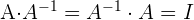
Die inverse Matrix kann auf zwei Arten berechnet werden: mithilfe des Gauß-Verfahrens oder mithilfe der Berechnung mit Determinanten.
Eigenschaften der inversen Matrix
1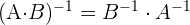
2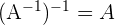
3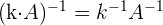
4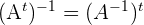
Berechnung mit Determinanten
Die Berechnung einer inversen matrix mit Determinanten sieht wie folgt aus: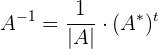
, mit
Um den Rechenvorgang besser verstehen zu können, beginnen wir mit einem Beispiel:
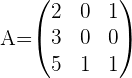
1 Berechne die Determinante der Matrix.
Sollte die Determinante Null ergeben, besitzt die Matrix keine Inverse.
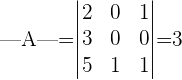
2 Ermittle die Adjunkte
Als Adjunkte bezeichnet man die Transponierte der Kofaktormatrix. Mit ihr kann die Inverse der Matrix berechnet werden.
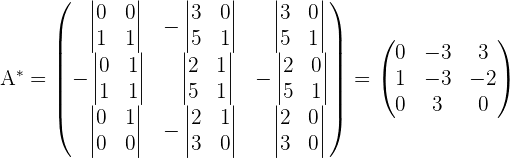
3 Berechne die Transponierte der adjunkten Matrix.
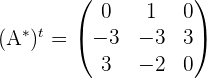
4 Die inverse Matrix besitzt den umgekehrten Wert ihrer Determinante mal der Transponierten ihrer Adjunkten..
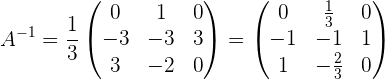
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
