Kapitel

Fall 1: Fläche zwischen einer positiven Funktion und der x-Achse
Wenn die Funktion auf einem Intervall  positiv ist, dann liegt der Graph der Funktion über der x-Achse. Der Flächeninhalt der Funktion ist gegeben durch:
positiv ist, dann liegt der Graph der Funktion über der x-Achse. Der Flächeninhalt der Funktion ist gegeben durch:

Um die Fläche zu berechnen, gehen wir wie folgt vor:
1 Wir berechnen die Schnittpunkte mit der  -Achse, indem wir
-Achse, indem wir  setzen und lösen die Gleichung.
setzen und lösen die Gleichung.
2 Die Fläche ist gleich dem la bestimmten Integral der Funktion, deren Integrationsgrenzen die Schnittpunkte sind.
Beispiel
1 Berechne den Flächeninhalt des Abschnitts, der durch den Graphen  und die
und die  -Achse definiert ist.
-Achse definiert ist.
Zunächst ermitteln wir die Schnittpunkte mit der  -Achse, um den Graphen darzustellen und die Integrationsgrenzen zu bestimmen.
-Achse, um den Graphen darzustellen und die Integrationsgrenzen zu bestimmen.

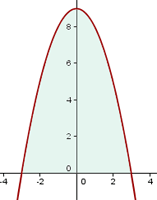
Da die Parabel symmetrisch zur  -Achse ist, entspricht die Fläche gleich dem Doppelten der Fläche zwischen
-Achse ist, entspricht die Fläche gleich dem Doppelten der Fläche zwischen  und
und  .
.
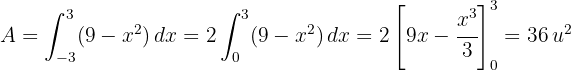
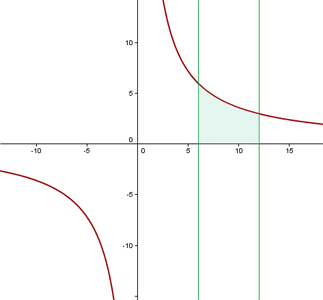
2 Berechne die durch den Graphen 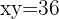 , die
, die  -Achse und folgende Geraden begrenzte Fläche:
-Achse und folgende Geraden begrenzte Fläche:  ,
,  .
.

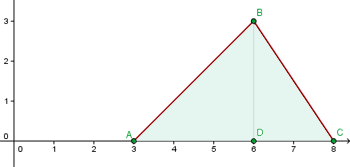
3 Berechne den Flächeninhalt des Dreiecks mit den Eckpunkten  .
.
Gleichung der Gerade, die durch  verläuft:
verläuft:

Gleichung der Geraden, die durch  verläuft:
verläuft:
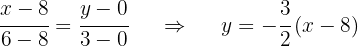
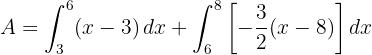
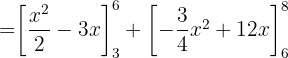
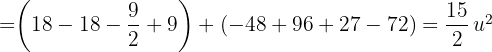
Fall 2: Fläche zwischen einer negativen Funktion und der x-Achse
Wenn die Funktion auf dem Intervall  negativ ist befindet sich der Graph der Funktin unterhalb der x-Achse. Der Flächeninhalt der Funktion ist gegeben durch:
negativ ist befindet sich der Graph der Funktin unterhalb der x-Achse. Der Flächeninhalt der Funktion ist gegeben durch:

Beispiele
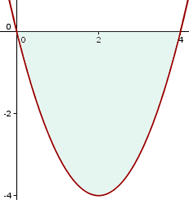
1 Berechne die Fläche zwischen dem Graphen 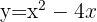 und der
und der  -Achse.
-Achse.

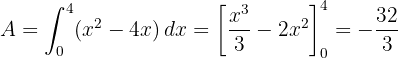
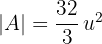
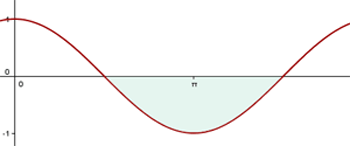
2 Berechne die Fläche zwischen dem Graphen el área limitada por la curva  und der
und der  -Achse im Bereich von
-Achse im Bereich von 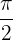 und
und 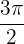 .
.
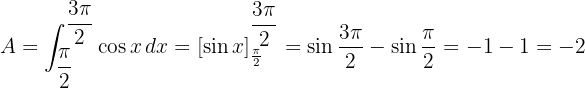
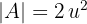
Fall 3: Die Funktion nimmt positive und negative Werte an
In diesem Fall befindet sich der Bereich oberhalb und unterhalb der x-Achse. Um die Fläche der Funktion zu berechnen gehen wir wie folgt vor:
1 Wir berechnen die Schnittpunkte mit der  -Achse, indem wir
-Achse, indem wir 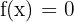 setzen und die Gleichung lösen.
setzen und die Gleichung lösen.
2 Wir orden die Nullstellen von klein nach groß und erhalten somit unsere Integrationsgrenzen.
3 Der Flächeninhalt ist gleich der la Summe der bestimmten Integrale im Betrag jedes Intervalls.
Beispiele
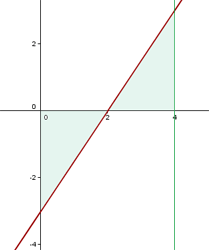
1 Berechne die Fläche zwischen der Geraden 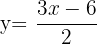 , der x-Achse und den entsprechenden Ordinaten zu
, der x-Achse und den entsprechenden Ordinaten zu  und
und  .
.



2 Berechne den Flächeninhalt des Bereichs der Ebene, der durch den Kreis  begrenzt wird..
begrenzt wird..
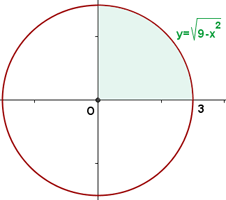
Die Fläche des Kreises ist das Vierfache der Fläche, die vom ersten 1. Quadranten und den Koordinatenachsen eingeschlossen wird.
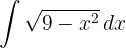
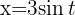
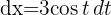
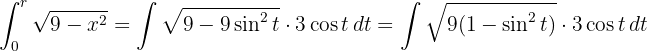
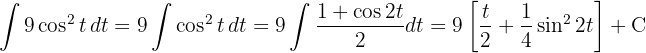
Bestimme die neuen Integrationsgrenzen.

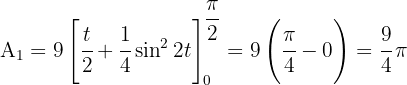
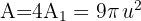
Mit KI zusammenfassen:












