Kapitel

Fläche unterhalb des Graphen einer Funktion, die positive Werte annimmt
Wenn die Funktion positive Werte auf einem Intervall 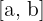 annimmt, dann liegt der Graph der Funktion über der x-Achse. Der Flächeninhalt der Funktion ist gegeben durch:
annimmt, dann liegt der Graph der Funktion über der x-Achse. Der Flächeninhalt der Funktion ist gegeben durch:
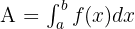
Um die Fläche zu bestimmen, gehen wir wie folgt vor:
1 Wir berechnen die Schnittpunkte mit der  -Achse, indem wir
-Achse, indem wir  setzen und die Gleichung lösen.
setzen und die Gleichung lösen.
2 Die Fläche ist gleich dem bestimmten Integral der Funktion. Die Integrationsgrenzen sind die Schnittpunkte.
Beispiele für Flächen, die durch positive Funktionen begrenzt sind
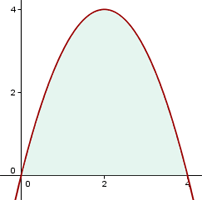
Berechne die Fläche, die durch den Graphen 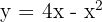 und die
und die  -Achse beschränkt ist
-Achse beschränkt ist
Zunächst berechnen wir die Schnittpunkte mit der x-Achse, um den Graphen darzustellen und die Integrationsgrenzen zu ermitteln. Das heißt, wir setzen die Funktion gleich 0 und lösen. 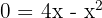
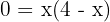
 y
y 
Wir berechnen das Integral:
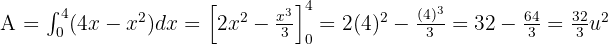
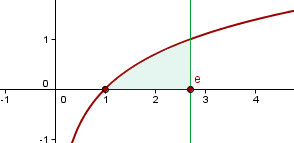
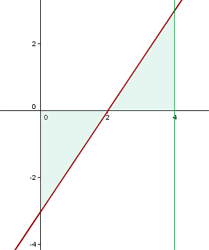
Ermittle den Flächeninhalt des Bereichs der Ebene, der von dem Graphen 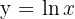 zwischen dem Schnittpunkt mit der
zwischen dem Schnittpunkt mit der  -Achse und dem Punkt
-Achse und dem Punkt  auf der x-Achse eingeschlossen wird.
auf der x-Achse eingeschlossen wird.
Zunächst berechnen wir den Schnittpunkt mit der x-Achse, d. h. wir setzen die Funktion gleich 0 und lösen.  Wir wenden das Exponential auf beiden Seiten an
Wir wenden das Exponential auf beiden Seiten an 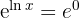
 . Da
. Da  , lautet der Schnittpunkt
, lautet der Schnittpunkt 
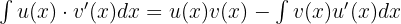 :
: 
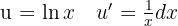

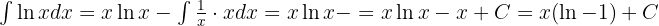 Somit gilt:
Somit gilt: 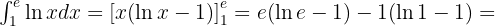
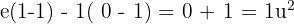
Fläche unterhalb des Graphen einer Funktion, die negative Werte annimmt
Wenn die Funktion auf einem Intervall 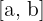 negative Werte annimmt, befindet sich der Funktionsgraph unterhalb der x-Achse. Die Fläche der Funktion ist gegeben durch:
negative Werte annimmt, befindet sich der Funktionsgraph unterhalb der x-Achse. Die Fläche der Funktion ist gegeben durch:

Beispiele für Flächen, die durch negative Funktionen begrenzt sind
Berechne die durch den Graphen 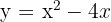 und die x-Achse beschränkte Fläche
und die x-Achse beschränkte Fläche
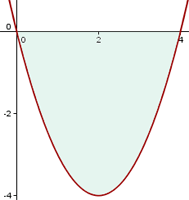
Zunächst berechnen wir die Schnittpunkte mit der x-Achse, um den Graphen darzustellen und die Integrationsgrenzen zu ermitteln. Das heißt, wir setzen die Funktion gleich 0 und lösen. 
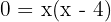
 y
y 
Wir berechnen das Integral:
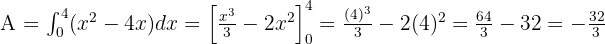
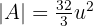
Berechne die Fläche, die durch den Graphen  und die x-Achse im Bereich zwischen
und die x-Achse im Bereich zwischen 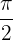 und
und 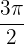 beschränkt ist.
beschränkt ist.
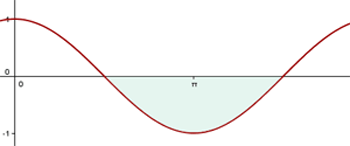
Wir lösen das Integral:
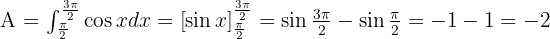

Fläche einer Funktion, die positive und negative Werte annimmt
In diesem Fall hat die Fläche Zonen oberhalb und unterhalb der x-Achse. Um die Fläche der Funktion zu berechnen, gehen wir wie folgt vor:
Wir berechnen die Schnittpunkte mit der x-Achse, indem wir  setzen und die Gleichung lösen.
setzen und die Gleichung lösen.
2 Wir ordnen die Nullstellen, die die Grenzen der Integration bilden, vom kleinsten zum größten Wert.
3 Die Fläche ist gleich der Summe der bestimmten Integrale im Betrag jedes Intervalls.
Berechne die Fläche der Bereiche der Ebene, die durch den Graphen 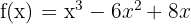 und die x-Achse begrenzt ist.
und die x-Achse begrenzt ist.
Zunächst ermitteln wir die Schnittpunkte mit der x-Achse, um den Graphen darzustellen und die Integrationsgrenzen zu berechnen. Das heißt, wir setzen die Funktion gleich 0 und lösen. 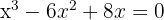


 und
und 
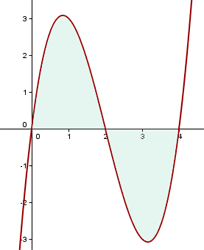
Wir sehen uns den Graphen an und müssen zwei Integrale berechnen: eines für den Fall, dass die Funktion positive Werte auf dem Intervall  annimmt und eines für den Fall, dass die Funktion negative Werte auf dem Intervall
annimmt und eines für den Fall, dass die Funktion negative Werte auf dem Intervall  annimmt.
annimmt.
Der Graph ist symmetrisch und die Fläche kann also wie folgt geschrieben werden: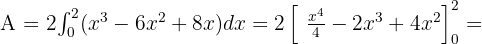
Beispiel
Fläche zwischen zwei Funktionen
Die Fläche zwischen zwei Funktionen ist gleich der Fläche der oberen Funktion minus der Fläche der unteren Funktion.
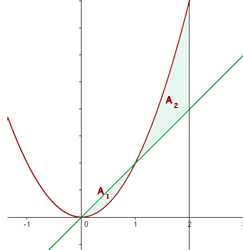
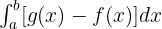
Berechne die Fläche des Kreises mit dem Radius r
Wir gehen von der Kreisgleichung 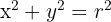 aus.
aus.
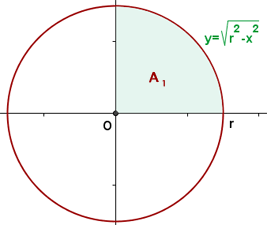
Die Fläche des Kreises ist viermal so groß wie die Fläche des 1. Quadranten.
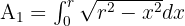
Wir berechnen das unbestimmte Integral durch Substitution:
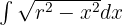

Somit
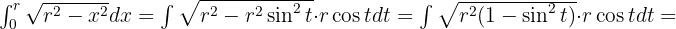
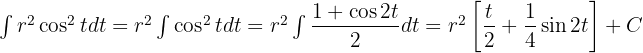
Wir ermitteln die neuen Integrationsgrenzen.

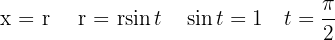
Schließlich

Da der Graph symmetrisch ist:
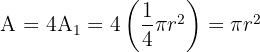
Mit KI zusammenfassen:












