Kapitel
- Irrationale Zahlen
- Die reellen Zahlen
- Zahlengerade
- Darstellung der reellen Zahlen
- Rechnen mit reellen Zahlen
- 1
- 2
- 3
- 4
- Division von reellen Zahlen
- Definition des Intervalls
- Offenes Intervall
- Abgeschlossenes Intervall
- Linksoffenes Intervall
- Rechtsoffenes Intervall
- Mathematische Notation für verschiedene Mengen
- Halbgeraden
- x > a
- x ≥ a
- x < a
- x ≤ a
- Betrag
- Distanz
- Definition der Umgebung
- Seitliche Umgebungen
- Eingeschränkte Umgebung

Irrationale Zahlen
Eine Zahl ist irrational, wenn sie unendlich viele nichtperiodische Nachkommastellen hat und daher nicht als Bruch ausgedrückt werden kann.
Die bekannteste irrationale Zahl ist π, die als das Verhältnis der Länge des Umfangs zu seinem Durchmesser definiert ist.
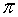
Weitere irrationale Zahlen sind:
Die Zahl e taucht bei Wachstumsprozessen, beim radioaktiven Zerfall und in der Oberleitungsformel auf, also der Kurve, die wir bei Stromleitungen sehen können.
e = 2,718281828459...
Der goldene Schnitt Φ, der von Künstlern aller Epochen (Phidias, Leonardo da Vinci, Albrecht Dürer, Dalí,...) für die Proportionen ihrer Werke verwendet wurde.
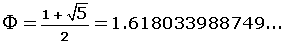
Die reellen Zahlen
Die Menge der rationalen und irrationalen Zahlen ist die Menge der reellen Zahlen, bezeichnet durch 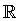
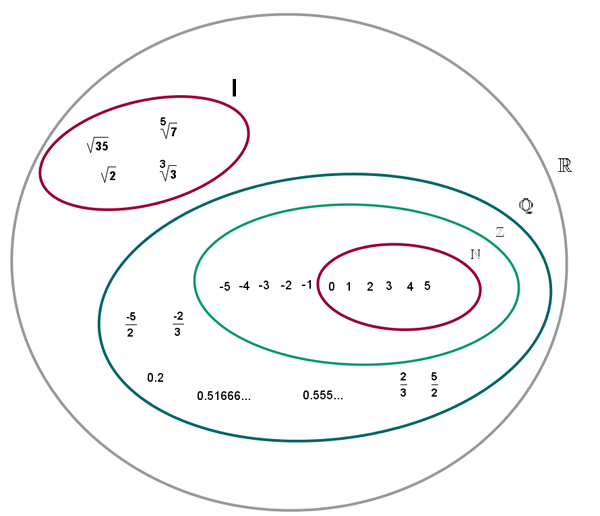
Mit reellen Zahlen können wir alle Rechenoperationen durchführen, mit Ausnahme des geradzahligen und negativen Radikanden und der Division durch 0.
Zahlengerade
Jeder reellen Zahl entspricht ein Punkt auf der Geraden und jedem Punkt auf der Geraden eine reelle Zahl.
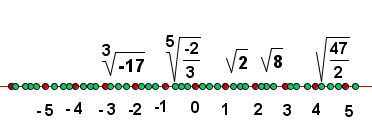
Darstellung der reellen Zahlen
Die reellen Zahlen können auf der Geraden mit beliebiger Annäherung dargestellt werden, aber es gibt Fälle, in denen wir sie genau darstellen können.
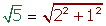
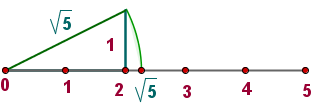
Rechnen mit reellen Zahlen
1
Addition von reellen Zahlen
Rechenregeln:
1 Intern:
Das Ergebnis der Addition zweier reeller Zahlen ist eine weitere reelle Zahl.
a + b 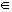
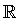
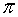
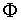
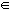
2 Assoziativ:
Die Art und Weise, wie die Summanden gruppiert sind, ändert nichts am Ergebnis.
(a + b) + c = a + (b + c) ·
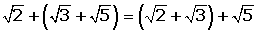
3 Kommutativ:
Die Reihenfolge der Summanden ändert nichts an der Summe.
a + b = b + a
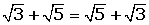
4 Neutrales Element:
Die 0 ist das neutrale Element der Summe, denn jede Zahl, die mit ihr addiert wird, ergibt die gleiche Zahl.
a + 0 = a
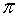
5 Gegenzahl:
Zwei Zahlen sind gegensätzlich, wenn ihre Addition 0 ergibt.
e − e = 0
Die Gegenzahl der Gegenzahl einer Zahl ist gleich der gleichen Zahl.
−(−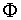
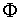
2
Differenz von reellen Zahlen
Die Differenz zweier reeller Zahlen ist definiert als die Summe des Minuenden plus die Gegenzahl des Subtrahenden.
a − b = a + (−b)
3
Produkt aus reellen Zahlen
Die Vorzeichenregel für das Produkt aus ganzen und rationalen Zahlen gilt auch für reelle Zahlen.
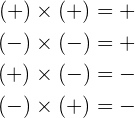
Rechengesetze:
1 Intern:
Das Ergebnis der Multiplikation zweier reeller Zahlen ist eine weitere reelle Zahl.
a · b
2 Assoziativ:
Die Art und Weise, wie die Faktoren gruppiert sind, ändert nichts am Ergebnis. Wenn a, b und c beliebige reelle Zahlen sind, gilt, dass:
(a · b) · c = a · (b · c)
(e · ) · 
3 Kommutativ:
Die Reihenfolge der Faktoren hat keinen Einfluss auf das Produkt.
a · b = b · a
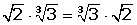
4 Neutrales Element:
Die 1 ist das neutrale Element der Multiplikation, denn jede Zahl, die mit ihr multipliziert wird, ergibt die gleiche Zahl.
a ·1 = a
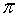
5 Gegenzahl:
Eine Zahl ist der Kehrwert der anderen, wenn ihre Multiplikation das Einheitselement ergibt.
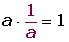
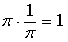
6 Distributiv:
Das Produkt einer Zahl mit einer Summe ist gleich der Summe der Produkte dieser Zahl mit jedem der Summanden.
a · (b + c) = a · b + a · c
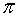
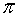
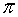
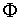
7 Gemeinsamen Faktor ausklammern:
Dies ist die Umkehrung des Distributivgesetzes.
Wenn mehrere Summanden einen gemeinsamen Faktor haben, können wir die Summe in ein Produkt umwandeln, indem wir diesen Faktor ausklammern.
a · b + a · c = a · (b + c)
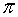
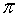
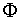
4
Division von reellen Zahlen
Die Division zweier reeller Zahlen ist definiert als das Produkt aus dem Dividenden und dem Kehrwert des Divisors.
Definition des Intervalls
Ein Intervall ist die Menge der reellen Zahlen, die zwischen zwei anderen gegebenen Zahlen liegen: a und b, die als Intervallgrenzen bezeichnet werden.
Offenes Intervall
Das offene Intervall (a, b) ist die Menge aller reellen Zahlen, die größer als a und kleiner als b sind.
(a, b) = {x / a < x < b}
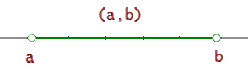
Abgeschlossenes Intervall
Das abgeschlossene Intervall [a, b] ist die Menge aller reellen Zahlen, die größer als oder gleich a und kleiner als oder gleich b sind.
[a, b] = {x / a ≤ x ≤ b}
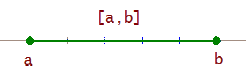
Linksoffenes Intervall
Das linksoffene Intervall, (a, b], ist die Menge aller reellen Zahlen größer als a und kleiner oder gleich b.
(a, b] = {x / a < x ≤ b}
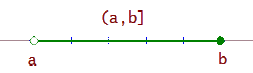
Rechtsoffenes Intervall
Das rechtsoffene Intervall [a, b) ist die Menge aller reellen Zahlen, die größer als oder gleich a und kleiner als b sind.
[a, b) = {x / a ≤ x < b}
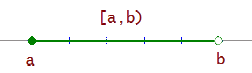
Mathematische Notation für verschiedene Mengen
Wenn wir eine Gruppe von Punkten benennen wollen, die aus zwei oder mehr dieser Intervalle besteht, verwenden wir das Vorzeichen 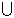
Halbgeraden
Eine Halbgerade bzw. ein Strahl wird durch eine Zahl bestimmt. Alle Zahlen, die größer (oder kleiner) sind als diese, liegen auf einer Halbgeraden.
x > a
(a, +∞) = {x / a < x < +∞}
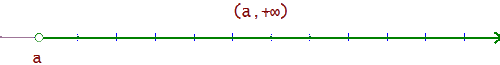
x ≥ a
[a, +∞) = {x / a ≤ x < +∞}
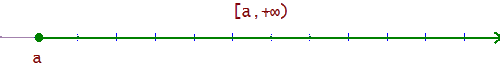
x < a
(-∞, a) = {x / -∞ < x < a}

x ≤ a
(-∞, a] = {x / -∞ < x ≤ a}

Betrag
Der Betrag einer reellen Zahl a, geschrieben |a|, ist die gleiche Zahl a, wenn a positiv oder null ist, und das Gegenteil von a, wenn a negativ ist.
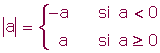
|5| = 5 |-5 |= 5 |0| = 0
|x| = 2 x = −2 x = 2
|x|< 2 − 2 < x < 2 x (−2, 2 )
|x|> 2 x< -2 ó x>2 (−∞, -2 ) (2, +∞)
|x −2 |< 5 − 5 < x − 2 < 5
− 5 + 2 < x < 5 + 2 − 3 < x < 7
Rechenregeln:
1 Gegenzahlen haben den gleichen Betrag.
|a| = |−a|
Beispiel: |5| = |−5| = 5
2 Der Betrag eines Produkts ist gleich dem Produkt der Beträge der Faktoren.
|a · b| = |a|· |b|
Beispiel:
|5 · (−2)| = |5| · |(−2)|
|−10| = |5| · |2|
10 = 10
3 Der Betrag einer Summe ist kleiner oder gleich der Summe der Beträge der Summanden.
|a + b| ≤ |a| + |b|
Beispiel:
|5 + (−2)| ≤ |5| + |(−2)|
|3| = |5| + |2|
3 ≤ 7
Distanz
Die Distanz zwischen zwei reellen Zahlen a und b, geschrieben d(a, b), ist definiert als der Betrag der Differenz der beiden Zahlen:
d(a, b) = |b − a|
Beispiel:
Die Distanz zwischen −5 und 4 ist:
d(−5, 4) = |4 − (−5)| =
= |4 + 5| = |9|
Definition der Umgebung
Das offene Intervall (a-r, a+r) wird als Umgebung mit Zentrum a und Radius r bezeichnet und mit Er(a) oder E(a,r) bezeichnet.
Er(a) = (a-r, a+r)
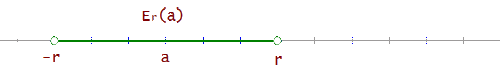
Umgebungen werden mithilfe des Betrags ausgedrückt.
Er(0) = (-r, r) wird als |x|<r ausgedrückt oder
-r < x < r.
Er(a) = (a-r, a+r) wird auch als |x-a|<r ausgedrückt oder
a − r < x < a+r.
Seitliche Umgebungen
Auf der linken Seite
Er(a-) = (a-r, a]
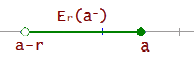
Auf der rechten Seite
Er(a+) = [a, a+r)
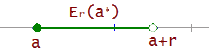
Eingeschränkte Umgebung
Sie wird verwendet, wenn man wissen möchte, was in der Nähe des Punktes passiert, ohne sich dafür zu interessieren, was am Punkt selbst passiert.
E r*(a) = { x (a − r, a + r), x ≠ a}
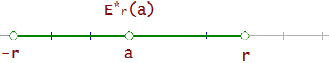
Mit KI zusammenfassen:













