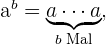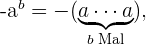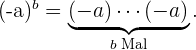Kapitel
Eine Multiplikation, die aus gleichen Faktoren besteht, kann als Potenz geschrieben werden:  , wobei
, wobei  , auch bekannt als Basis, die Zahl ist, die wiederholt wird, und
, auch bekannt als Basis, die Zahl ist, die wiederholt wird, und  , der Exponent, die Anzahl der Wiederholungen des Faktors ist. Zum Beispiel
, der Exponent, die Anzahl der Wiederholungen des Faktors ist. Zum Beispiel
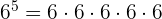
In diesem Beispiel haben wir die Basis  und den Exponenten
und den Exponenten  .
.

Potenzen mit ganzzahligem Exponenten
Potenz mit positivem ganzzahligen Exponenten
Wenn der Exponent einer Potenz eine positive ganze Zahl ist, ergibt sich aus der Notation
Um das Vorzeichen einer Potenz mit einem ganzzahligen Exponenten zu bestimmen, müssen wir Folgendes berücksichtigen:
1 Potenzen mit geradem Exponenten sind immer positiv. Wenn wir also eine Potenz  haben, gilt:
haben, gilt:
- Wenn
 positiv ist und
positiv ist und  gerade, so ist
gerade, so ist  positiv.
positiv. - Wenn
 negativ ist und
negativ ist und  gerade, so ist
gerade, so ist  positiv.
positiv.
Beispiel:
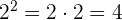

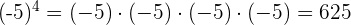
2 Potenzen mit ungeradem Exponenten haben immer dasselbe Vorzeichen wie ihre Basis. Wenn wir also eine Potenz  haben, gilt:
haben, gilt:
- Wenn
 positiv ist und
positiv ist und  ungerade, so ist
ungerade, so ist  positiv.
positiv. - Wenn
 negativ ist und
negativ ist und  ungerade, so ist
ungerade, so ist  negativ.
negativ.
Beispiel:
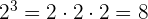
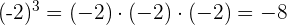
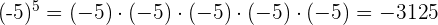
Potenz mit ganzzahligem negativen Exponenten
Eine Potenz mit negativem Exponenten ist gleich dem multiplikativen Kehrwert der Basis der Potenz, erhöht auf den positiven Exponenten (vorausgesetzt, die Basis ist ungleich 0). Wir haben also
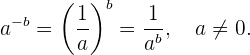
Und für 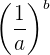 sind die gleichen Eigenschaften wie oben für positive Exponenten erfüllt.
sind die gleichen Eigenschaften wie oben für positive Exponenten erfüllt.
Beispiel:

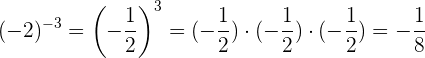
Potenzen von rationalen Zahlen
Potenz einer positiven Zahl
Wenn die Basis einer Potenz eine Bruchzahl ist, erhöhen wir sowohl den Zähler als auch den Nenner auf den Exponenten.

Beispiel:
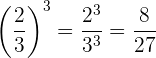
Potenz mit Bruch als Basis und negativem Exponenten
Eine Potenz mit einem Bruch als Basis und einem negativen Exponenten ist gleich dem multiplikativen Kehrwert der Basis, erhöht um den positiven Exponenten. Zur Erinnerung: Die Umkehrung eines Bruchs ist gleichbedeutend mit der Vertauschung von Zähler und Nenner, d. h. der Kehrwert von 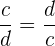 . Wir haben also
. Wir haben also
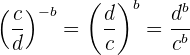
Beispiel:
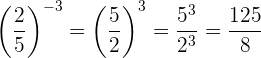
Potenzen mit rationalem Exponenten oder Bruch als Exponent
Eine Potenz mit einem Bruch als Exponent ist gleich einer Wurzel, deren Wurzelexponent der Nenner des Bruchs und der Exponent des Radikanden der Zähler ist.
Potenz mit positivem rationalen Exponenten
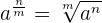
Beispiele:

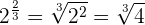
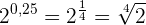
In diesem Fall wandeln wir den Exponenten, der eine Dezimalzahl ist, in den entsprechenden Bruch um.
Potenz mit negativem rationalen Exponenten
Wenn der Exponent ein negativer Bruch ist, ist es wie in den vorherigen Fällen gleichbedeutend damit, den multiplikativen Kehrwert der Basis auf den positiven Exponenten zu erhöhen. Wir haben also
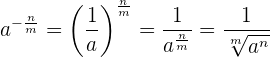
Beispiel:
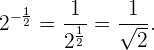
Eigenschaften von Potenzen
Eine Zahl hoch 0 ist gleich 1.

Zum Beispiel:  .
.
Eine Zahl mit dem Exponenten 1 ist gleich ihrer selbst.
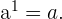
Zum Beispiel: 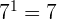 .
.
Produkt von Potenzen mit gleicher Basis.
Wenn wir zwei Potenzen mit der gleichen Basis multiplizieren, ist das Ergebnis eine weitere Potenz mit der gleichen Basis, die auf die Summe der ursprünglichen Exponenten erhöht wird.

Beispiel:
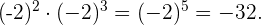

Division von Potenzen mit gleicher Basis
Bei der Division zweier Potenzen mit der gleichen Basis ist das Ergebnis eine weitere Potenz mit der gleichen Basis, die auf den Exponenten des Zählers minus den Exponenten des Nenners erhöht wird.
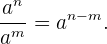
Beispiel:
 .
.

Potenz einer Potenz
Wenn wir eine Potenz einer Potenz haben, ist das Ergebnis eine andere Potenz mit der gleichen Basis, die auf das Produkt der Exponenten erhöht wird.

Beispiel:
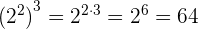 .
.
 .
.
Produkt von Potenzen mit gleichem Exponenten
Bei der Multiplikation zweier Potenzen mit dem gleichen Exponenten ist das Ergebnis eine neue Potenz, deren Basis die Multiplikation der ursprünglichen Basen mit dem gleichen Exponenten ist.

Ejemplo:
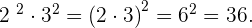
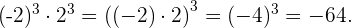
Quotient von Potenzen mit gleichem Exponenten
Wenn wir den Quotienten zweier Potenzen mit dem gleichen Exponenten haben, ist das Ergebnis eine neue Potenz, bei der die Basis der Quotient der ursprünglichen Basen ist, die auf den gleichen Exponenten erhöht wurden.

Beispiel:
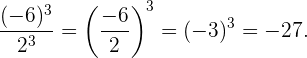
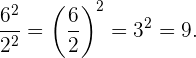
Mit KI zusammenfassen: