Kapitel

Imaginäre Einheit
Dies ist die Bezeichnung für die Zahl 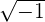 und sie wird mit dem Buchstaben
und sie wird mit dem Buchstaben  angegeben
angegeben
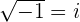
Die Kubikwurzel aus  ist weder eine imaginäre noch eine komplexe Zahl.
ist weder eine imaginäre noch eine komplexe Zahl.
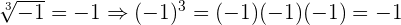
Beispiele mit imaginärer Einheit
1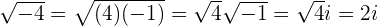
2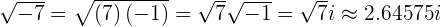
3
4 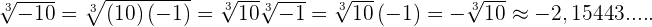
Komplexe Zahl
Die Zahl 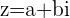 wird als komplexe Zahl in binomischer oder binomialer Form bezeichnet. Im Allgemeinen wird jede komplexe Zahl mit dem Buchstaben
wird als komplexe Zahl in binomischer oder binomialer Form bezeichnet. Im Allgemeinen wird jede komplexe Zahl mit dem Buchstaben  angegeben.
angegeben.
Die Zahl  ist der reelle Teil der komplexen Zahl und wird mit
ist der reelle Teil der komplexen Zahl und wird mit  angegeben, während die Zahl
angegeben, während die Zahl  der imaginäre Teil der komplexen Zahl ist und mit
der imaginäre Teil der komplexen Zahl ist und mit  angegeben wird.
angegeben wird.
Wenn der imaginäre Teil einer komplexen Zahl null ist, d. h.  , wird sie zu einer reellen Zahl
, wird sie zu einer reellen Zahl  , da
, da 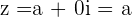 .
.
Wenn der reelle Teil einer komplexen Zahl null ist, d. h. 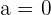 , wird die komplexe Zahl zu
, wird die komplexe Zahl zu  . Man sagt, dass die Zahl eine rein imaginäre Zahl ist.
. Man sagt, dass die Zahl eine rein imaginäre Zahl ist.
Im Allgemeinen wird die Menge aller komplexen Zahlen mit dem Symbol 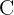 angegeben. Formal wird sie unter Verwendung der Mengenschreibweise wie folgt angegeben:
angegeben. Formal wird sie unter Verwendung der Mengenschreibweise wie folgt angegeben:
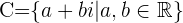
Die komplexen Zahlen 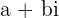 und
und 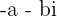 werden Gegenzahlen genannt.
werden Gegenzahlen genannt.
Die komplexen Zahlen  und
und  werden konjugierte komplexe Zahlen genannt.
werden konjugierte komplexe Zahlen genannt.
Zwei komplexe Zahlen sind gleich, wenn sie den gleichen reellen Anteil und den gleichen imaginären Anteil haben, das heißt:

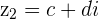
mit  oder
oder 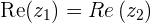 und
und  oder
oder 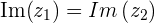
Grafische Darstellung der komplexen Zahlen
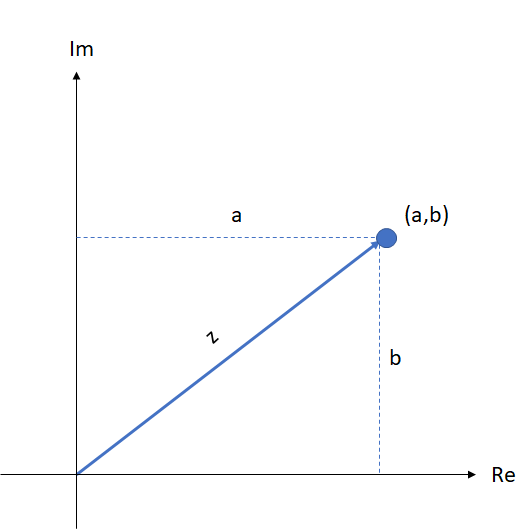
Die komplexen Zahlen werden in der kartesischen Ebene in Form eines Ortsvektors dargestellt, d. h. eines Vektors, dessen Anfangspunkt der Ursprung und dessen Endpunkt der Punkt  ist, auch Affix der komplexen Zahl genannt. Die
ist, auch Affix der komplexen Zahl genannt. Die  -Achse wird reelle Achse und die
-Achse wird reelle Achse und die  -Achse imaginäre Achse genannt.
-Achse imaginäre Achse genannt.
Potenzen der imaginären Einheit

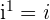
 , da
, da 
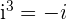 , da
, da 
 , da
, da  oder
oder 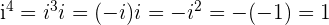
Beispiele für höhere Potenzen der komplexen Zahlen
1 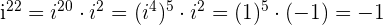
2 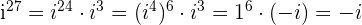
3 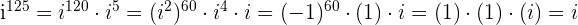
4
Rein imaginäre Zahlen
Eine rein imaginäre Zahl wird wie folgt angegeben:
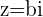 ,
,
wobei:
 eine reelle Zahl ist.
eine reelle Zahl ist.
 ist die imaginäre Einheit.
ist die imaginäre Einheit.
Wir beachten, dass der reelle Teil  ist, d. h,
ist, d. h, 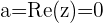 . Komplexe Zahlen, deren reeller Teil ungleich 0 ist, können auch einfach als imaginäre Zahlen bezeichnet werden.
. Komplexe Zahlen, deren reeller Teil ungleich 0 ist, können auch einfach als imaginäre Zahlen bezeichnet werden.
Rechenoperationen mit komplexen Zahlen in binomischer Form
Addition und Subtraktion von komplexen Zahlen
Die Regel für die Addition oder Subtraktion zweier komplexer Zahlen 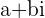 und
und  besteht darin, den reellen Teil der einen mit dem reellen Teil der anderen und den imaginären Teil der einen mit dem imaginären Teil der anderen zu addieren/subtrahieren.
besteht darin, den reellen Teil der einen mit dem reellen Teil der anderen und den imaginären Teil der einen mit dem imaginären Teil der anderen zu addieren/subtrahieren.
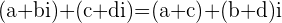

Wenn die Addition und Subtraktion mehrerer komplexer Zahlen kombiniert wird, addiert und/oder subtrahiert man die reellen Teile mit den reellen Teilen und die imaginären Teile mit den imaginären Teilen.
Beispiele:
1 
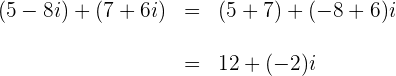
2 

3
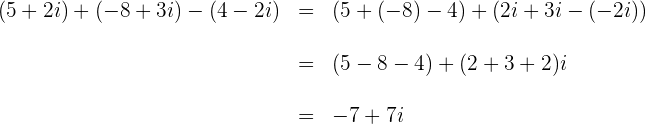
Die Addition und Subtraktion komplexer Zahlen kann auch als Addition und Subtraktion von Polynomen durchgeführt werden, da komplexe Zahlen in binomischer Form ausgedrückt werden.
Beispiel:

Produkt komplexer Zahlen
Das Produkt oder die Multiplikation komplexer Zahlen, die in binomischer Form ausgedrückt sind, erfolgt nach folgender Formel:
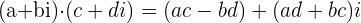
oder sie kann auch als Produkt von Binomien durchgeführt werden.
Beispiel nach der Formel:

Beispiel für ein Produkt aus Binomen:
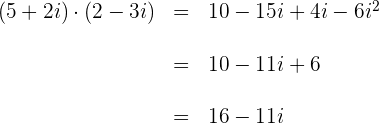
Division komplexer Zahlen
Die Division zweier komplexer Zahlen, die als Bruch ausgedrückt werden, erfolgt durch Multiplikation des Zählers und des Nenners des Bruchs mit der konjugierten komplexen Zahl des Nenners und anschließende Vereinfachung, bis das Ergebnis in der Form 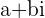 ausgedrückt wird.
ausgedrückt wird.
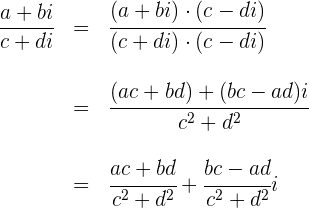
Beispiele:
1 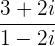
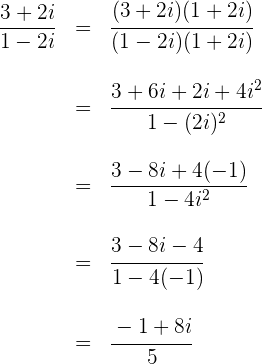
2 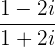
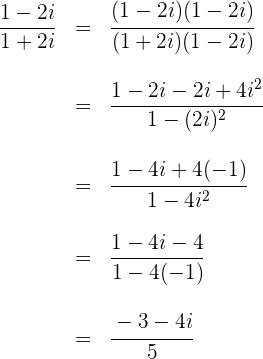
Betrag und Argument komplexer Zahlen
Der Betrag einer komplexen Zahl (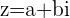 ), der grafisch dargestellt wird, ist die Länge des Vektors von seinem Anfangspunkt (Ursprung) bis zu seinem Endpunkt
), der grafisch dargestellt wird, ist die Länge des Vektors von seinem Anfangspunkt (Ursprung) bis zu seinem Endpunkt  . Er wird mit
. Er wird mit 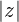 angegeben. Wendet man den Satz des Pythagoras auf das Dreieck
angegeben. Wendet man den Satz des Pythagoras auf das Dreieck 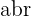 in der folgenden Abbildung an, erhält man die Formel zur Berechnung des Betrags einer komplexen Zahl:
in der folgenden Abbildung an, erhält man die Formel zur Berechnung des Betrags einer komplexen Zahl:
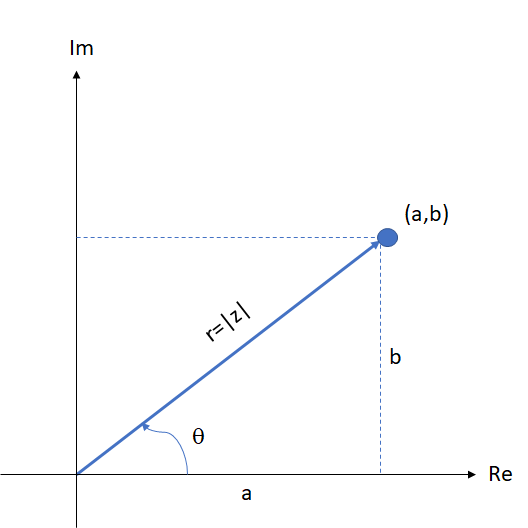
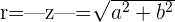
Das Argument einer komplexen Zahl ist der positive Winkel (der sich gegen den Uhrzeigersinn dreht), den der Vektor mit dem positiven Teil der reellen Achse bildet. Es wird mit 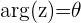 angegeben und anhand der folgenden Formel berechnet, abhängig von dem Quadranten, in dem sich die komplexe Zahl befindet.
angegeben und anhand der folgenden Formel berechnet, abhängig von dem Quadranten, in dem sich die komplexe Zahl befindet.
Erster Quadrant
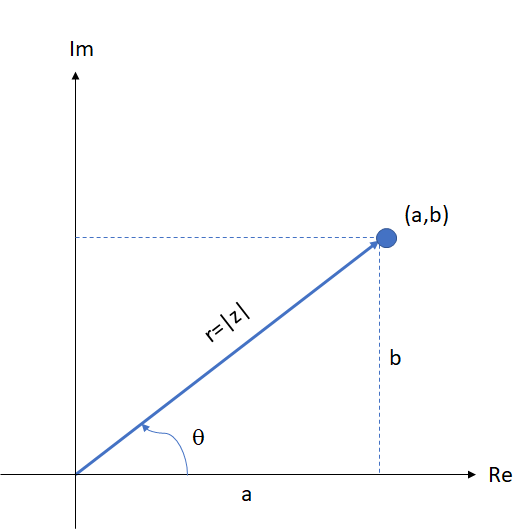
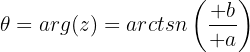
Zweiter Quadrant
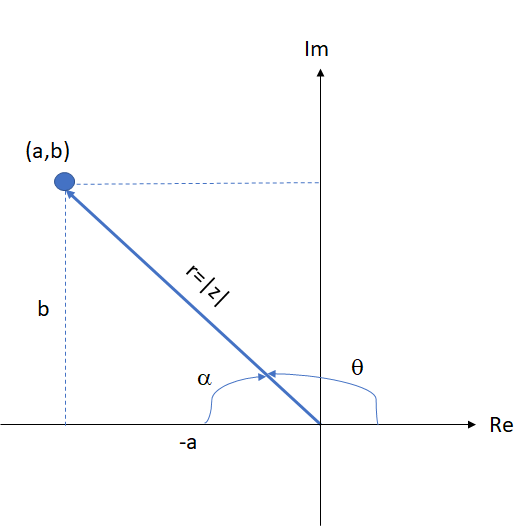
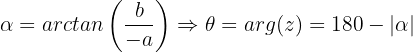
Dritter Quadrant
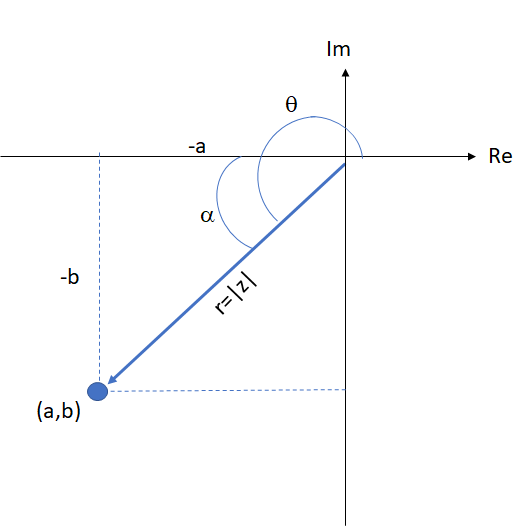
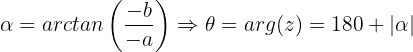
Vierter Quadrant
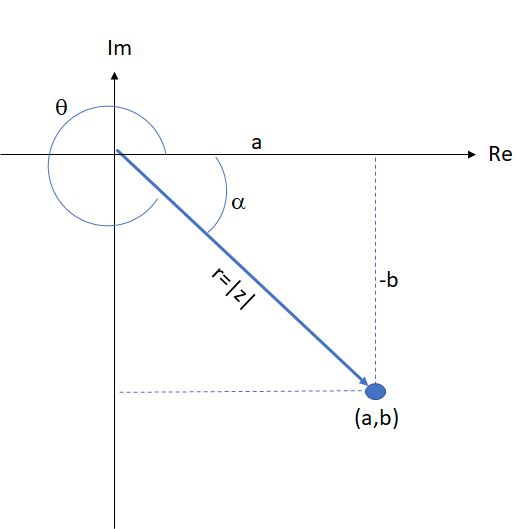
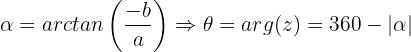
Beispiele: Wir berechnen den Betrag und das Argument der folgenden komplexen Zahlen. Außerdem stellen wir sie grafisch dar.
1 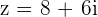
Wir berechnen den Betrag

Wir berechnen das Argument
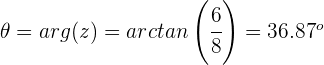
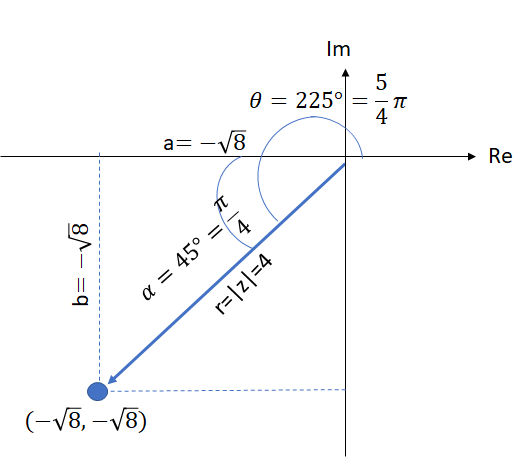
Grafische Darstellung
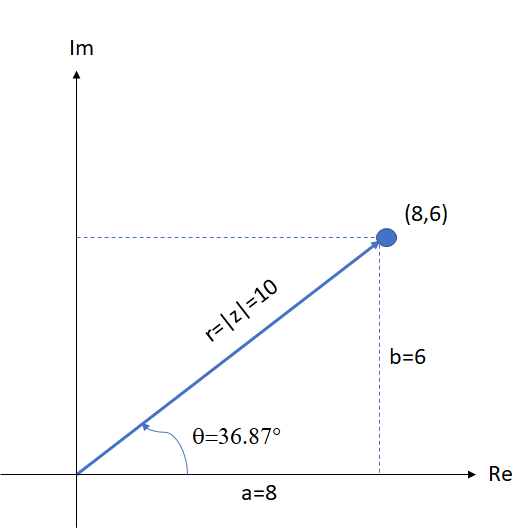
2 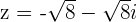
Wir berechnen den Betrag
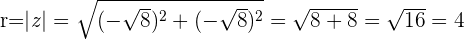
Wir berechnen das Argument
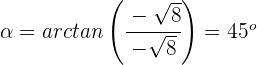
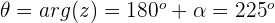
Grafische Darstellung
Komplexe Zahlen in polarer und trigonometrischer Form
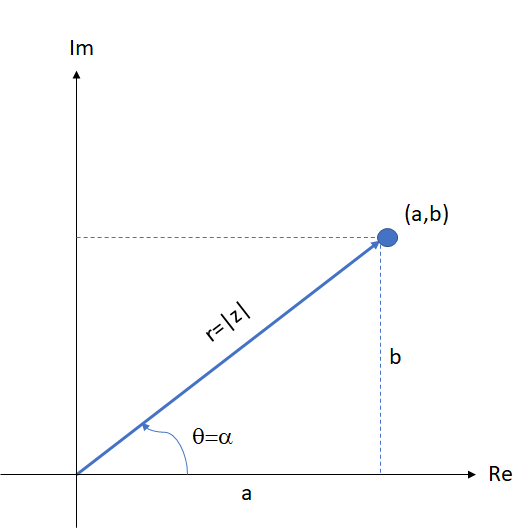
Um den reellen und den imaginären Teil  bzw.
bzw.  der komplexen Zahl in Abhängigkeit von ihrem Betrag und ihrem Argument zu erhalten, werden die Definitionen der Sinus- und Kosinusfunktionen auf den Winkel
der komplexen Zahl in Abhängigkeit von ihrem Betrag und ihrem Argument zu erhalten, werden die Definitionen der Sinus- und Kosinusfunktionen auf den Winkel  im Dreieck
im Dreieck 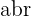 in der obigen Abbildung angewendet.
in der obigen Abbildung angewendet.

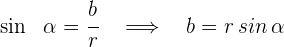
Anschließend wird die trigonometrische und polare Form der ganzen Zahl wie folgt ausgedrückt:
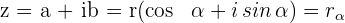
In der folgenden Tabelle sind die quadratischen (binomischen), polaren und trigonometrischen Formen einer beliebigen komplexen Zahl zusammengefasst.
| binomisch | 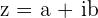 |
|---|---|
| polar | 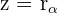 |
| trigonometrisch | 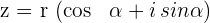 |
Gleiche, konjugierte und entgegengesetzte komplexe Zahlen in trigonometrischen und polaren Formen
Die folgende Grafik zeigt sowohl die polare als auch die trigonometrische Darstellung einer komplexen Zahl 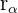 , ihrer komplexen Konjugierten
, ihrer komplexen Konjugierten 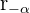 und ihrer komplexen Gegenzahl
und ihrer komplexen Gegenzahl 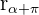 .
.
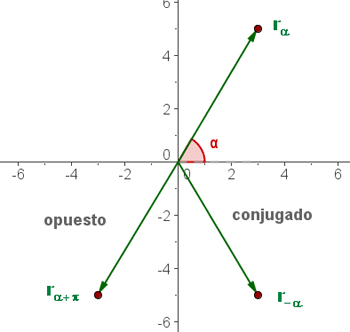
Gleiche komplexe Zahlen
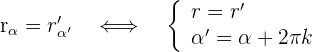

Konjugierte komplexe Zahlen


Komplexe Gegenzahlen


Produkt komplexer Zahlen in Polarform
Formel

Beispiele:
1 

2 

Produkt einer komplexen Zahl mit dem Betrag 1
Wenn man eine komplexe Zahl multiplicar un número complejo 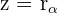 mit
mit  multipliziert, wird
multipliziert, wird  um einen Winkel
um einen Winkel  um den Ursprung gedreht.
um den Ursprung gedreht.
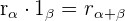
Quotient komplexer Zahlen in Polarform
Formel:

Beispiele:
1 

2 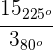
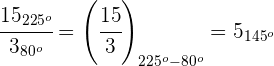
Potenz komplexer Zahlen in Polarform
Formel:

Beispiele:
1 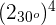
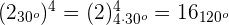
2 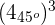

Moivrescher Satz
Der Moivresche Satz wird verwendet, um positive ganzzahlige Potenzen von komplexen Zahlen in trigonometrischer Form zu erhalten.
Die Formel lautet:
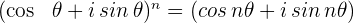
Bei Anwendung auf die  -te Potenz einer komplexen Zahl, ausgedrückt in ihrer Polarform:
-te Potenz einer komplexen Zahl, ausgedrückt in ihrer Polarform:
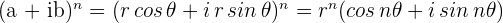
Beispiel:
Die Potenzierung der folgenden komplexen Zahl, ausgedrückt in der Binomialform, soll mithilfe der trigonometrischen Form und des Moivreschen Satzes durchgeführt werden, da die Verwendung der Binomialerweiterung etwas mühsam und zeitaufwändig wäre.

Schritt 1. Der Betrag und das Argument der Basis der Potenzierung, d. h. die komplexe Zahl ohne Exponent, werden berechnet.
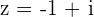
Betrag:

Argument:
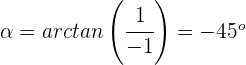
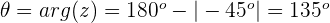
Schritt 2. Die komplexe Zahl wird in ihrer trigonometrischen Form ausgedrückt
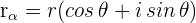
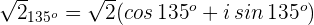
Schritte 3. Wir wenden den Moivreschen Satz an.
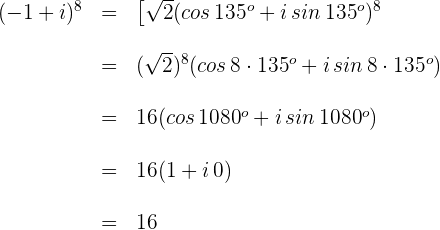
Schritt 4. Wir schreiben das Ergebnis.

n-te Wurzel komplexer Zahlen in Polarform
Jede komplexe Zahl (außer 0) hat genau  unterschiedliche Wurzeln.
unterschiedliche Wurzeln.
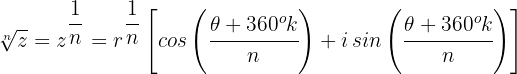

Beispiel:

Schritt 1. Der Betrag und das Argument der komplexen Zahl, aus der die sechste Wurzel gezogen werden soll, werden berechnet.

Betrag
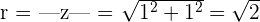
Argument
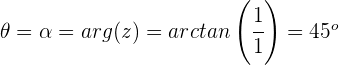
Schritt 2. Man setzt die Daten in die Formel ein, um die 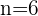 n-ten Wurzeln der komplexen Zahl
n-ten Wurzeln der komplexen Zahl  zu ermitteln.
zu ermitteln.
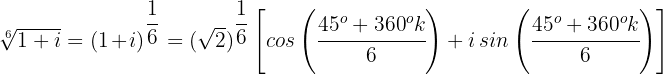
Paso 3. Der Wert von  wird von
wird von 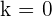 bis
bis  variiert, um die
variiert, um die  n-ten Wurzeln von
n-ten Wurzeln von  zu ermitteln
zu ermitteln
Für 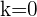
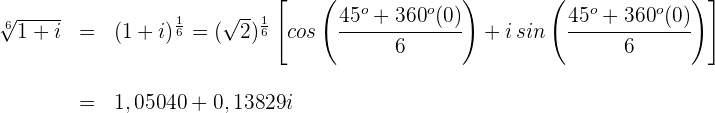
Para 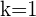
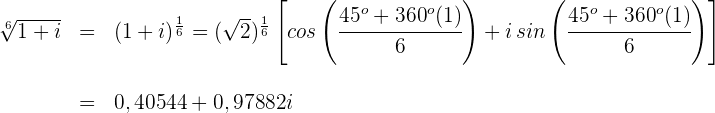
Para 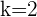
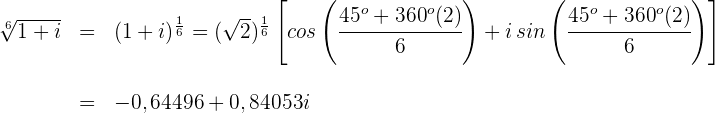
Für 
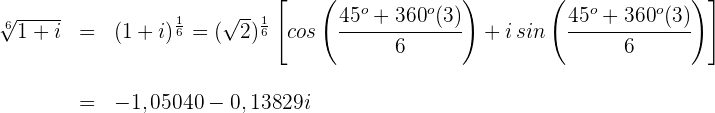
Für 
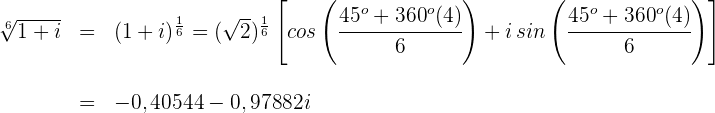
Für 
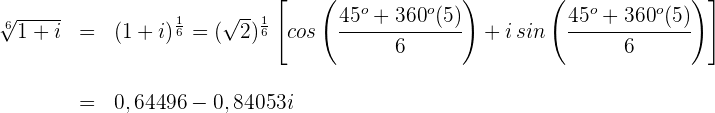
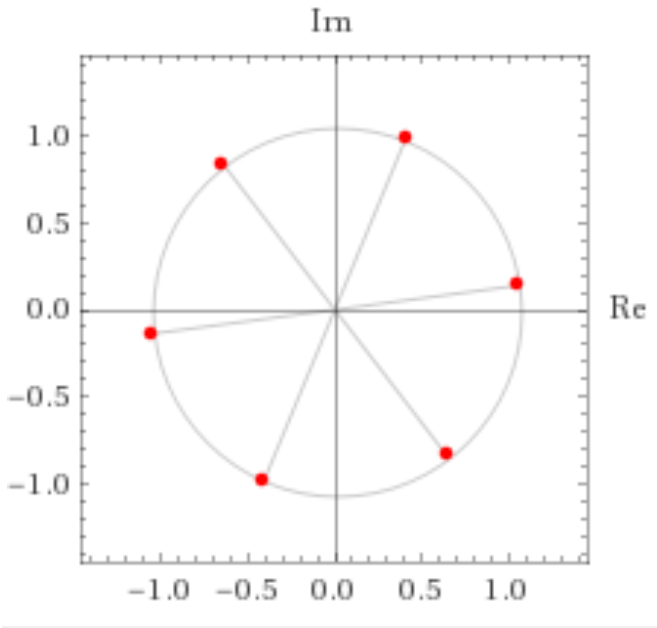
Grafische Darstellung der  Wurzeln der komplexen Zahl
Wurzeln der komplexen Zahl 
Mit KI zusammenfassen:













