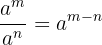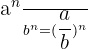Kapitel

Rationale Zahlen
Rationale Zahlen sind Zahlen, die durch den Quotienten zweier ganzer Zahlen dargestellt werden können, oder genauer gesagt, die als Quotient einer ganzen Zahl und einer positiven natürlichen Zahl dargestellt werden können. Das heißt, wir können sie als  mit
mit  ganzen Zahlen schreiben und
ganzen Zahlen schreiben und  .
.
Irrationale Zahlen
Eine Zahl ist irrational, wenn sie unendlich viele nichtperiodische Nachkommastellen hat und daher nicht als Bruch  mit
mit  ganzen Zahlen ausgedrückt werden kann und
ganzen Zahlen ausgedrückt werden kann und  .
.
Reelle Zahlen
Die Menge der rationalen und irrationalen Zahlen ist die Menge der reellen Zahlen und wird mit  angegeben.
angegeben.
Es gibt zum Beispiel Rechenoperationen, die in der Menge der reellen Zahlen nicht möglich sind. Zum Beispiel:
- Wurzelziehen mit geradem Wurzelexponenten und negativem Radikanden. In diesem Fall gibt es keine Lösung in der Menge der reellen Zahlen
- Division durch 0. Wenn der Divisor 0 ist, ist das Ergebnis unbestimmt.
Intervalle
Intervalle werden durch zwei Zahlen bestimmt, die als Extremwerte bezeichnet werden. In einem Intervall gibt es alle Zahlen, die zwischen den beiden liegen, und auch die Extremwerte können enthalten sein.
Es gibt verschiedene Arten von Intervallen:
1 Offenes Intervall: Menge aller reellen Zahlen, die größer als a und kleiner als b sind
2 Abgeschlossenes Intervall: este incluye los extremos del intervalo y los valores entre ellos, se expresa
3 Halboffenes Intervall: In halboffenen Intervallen wird nur ein Extremwert einbezogen und der andere ausgeschlossen. Wir haben
- Linksoffenes Intervall

- Rechtsoffenes Intervall

4 Unendliche Intervalle:
- wenn
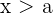 ,
,
- wenn
 ,
,
- wenn
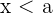 ,
,
- wenn
 ,
,
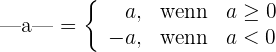
Eigenschaften
Wenn  und
und  reelle Zahlen sind
reelle Zahlen sind
 ,
, ,
, .
.
Wir können den Betrag mit Begriffen wie dem Abstand zwischen zwei Punkten auf der Zahlengerade verknüpfen. In diesem Fall wäre der Abstand zwischen zwei reellen Zahlen  und
und  , angegeben mit
, angegeben mit  ,
,
Umgebungen
Das offene Intervall  wird als Umgebung mit dem Zentrum Se llama entorno de centro
wird als Umgebung mit dem Zentrum Se llama entorno de centro  und dem Radius
und dem Radius  bezeichnet. Sie wird mit
bezeichnet. Sie wird mit 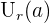 oder
oder 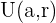 angegeben. Das heißt
angegeben. Das heißt 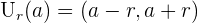 .
.
Es gibt verschiedene Umgebungen
1 Seitliche Umgebungen:
- auf der linken Seite

- auf der rechten Seite

2 Eingeschränkte Umgebung: Sie wird verwendet, wenn man wissen möchte, was in der Nähe des Punktes passiert, ohne sich dafür zu interessieren, was am Punkt selbst passiert

Potenzen
Eine Potenz ist ein Ausdruck der Form  , wobei
, wobei  die Basis und
die Basis und  der Exponent ist.
der Exponent ist.
Ganzzahliger Exponent
Wenn der Exponent eine natürliche Zahl  ist, gibt dies an, wie oft die Basis
ist, gibt dies an, wie oft die Basis  mit sich selbst multipliziert wird. Zum Beispiel
mit sich selbst multipliziert wird. Zum Beispiel
Wenn  eine positive ganze Zahl ist,
eine positive ganze Zahl ist,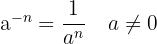
Rationaler Exponent
Wenn der Exponent rational ist, gilt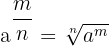
Eigenschaften
Wurzeln
Eine Wurzel ist ein Ausdruck der Form  , wobei
, wobei  und
und  . Außerdem ist
. Außerdem ist  der Radikand und
der Radikand und  der Wurzelexponent. Damit die Rechenoperation in den reellen Zahlen gültig ist, wenn
der Wurzelexponent. Damit die Rechenoperation in den reellen Zahlen gültig ist, wenn  negativ ist, muss
negativ ist, muss  ungerade sein.
ungerade sein.
Äquivalente Wurzeln
Beachte, dass eine Potenz mit einem rationalen Exponenten mit einer Wurzel gleichzusetzen ist. Unter Berücksichtigung dieser Tatsache und der Eigenschaft von Brüchen, die besagt, dass der Bruch äquivalent ist, wenn man Zähler und Nenner mit der gleichen Zahl multipliziert, ergibt sich Folgendes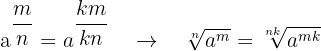
mit  und
und 
Multipliziert oder dividiert man den Wurzelexponenten und den Exponenten des Radikanden durch dieselbe natürliche Zahl, so erhält man eine weitere äquivalente Wurzel.
Vereinfachung von Wurzeln
Wenn es eine natürliche Zahl gibt, die den Wurzelexponenten und den Exponenten des Radikanden teilt, erhält man eine vereinfachte Wurzel.
Wurzeln gleichnamig machen
1Wir ermitteln das kleinste gemeinsame Vielfache der Wurzelexponenten. Dies ist dann unser Wurzelexponent
2Wir dividieren den gemeinsamen Wurzelexponenten durch jeden der Wurzelexponenten. Jedes Ergebnis multiplizieren wir dann mit dem entprechenden Exponenten.
Faktoren außerhalb der Wurzel
Zunächst wird der Radikand in Faktoren zerlegt und wenn:
1 Ein Exponent kleiner als der Wurzelexponent ist: Der entsprechende Faktor bleibt im Radikanden.
2 Ein Exponent gleich dem Wurzelexponenten ist: Der entsprechende Faktor verlässt den Radikanden.
3 Ein Exponent größer als der Wurzelexponent ist: Dieser Exponent wird durch den Wurzelexponenten dividiert. Der erhaltene Quotient ist der Exponent des Faktors außerhalb des Radikanden und der Rest ist der Exponent des Faktors innerhalb des Radikanden.
Faktoren unter die Wurzel bringen
Um Faktoren unter eine Wurzel zu bringen, werden die Faktoren auf den Wurzelexponenten der Wurzel angehoben
Rechnen mit Wurzeln
1 Addition: Zwei Wurzeln können nur dann addiert (oder subtrahiert) werden, wenn es sich um ähnliche Wurzeln handelt, d. h. wenn es sich um Wurzeln mit demselben Wurzelexponenten und demselben Radikanden handelt.
2 Multiplikation:
- Wurzeln mit gleichem Wurzelexponenten: zur Multiplikation von Wurzeln mit gleichem Wurzelexponenten multipliziert man die Radikanden und lässt den Wurzelexponenten unverändert

- Wurzeln mit unterschiedlichem Wurzelexponenten: Zunächst werden sie auf einen gemeinsamen Wurzelexponenten gebracht und dann multipliziert.
3 Division:
- Wurzeln gleichem Wurzelexponenten: Um Wurzeln mit gleichem Wurzelexponenten zu dividieren, dividiert man die Radikanden und lässt den Wurzelexponenten gleich.
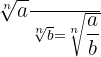
- Wurzeln mit unterschiedlichem Wurzelexponenten: Zunächst werden sie auf einen gemeinsamen Wurzelexponenten gebracht und dann dividiert.
4 Potenzen: Um eine Wurzel auf eine Potenz zu erhöhen, wird der Radikand auf diese Potenz erhöht und der Wurzelexponent bleibt gleich
4 Wurzelziehen: Die Wurzel Wurzel ist eine andere Wurzel mit gleichem Radikanden, deren Wurzelexponent das Produkt der beiden Wurzelexponenten ist
Rationalisieren
Hierbei werden die Wurzeln aus dem Nenner entfernt, was die Berechnung von Rechenoperationen wie der Addition von Brüchen erleichtert.
Wir können drei Fälle unterscheiden:
1Rationalisieren vom Typ 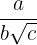 ;
;
Der Zähler und der Nenner werden mit  multipliziert
multipliziert
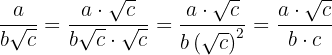
2 Rationalisieren vom Typ 
Der Zähler und der Nenner werden mit 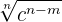 multipliziert
multipliziert

3Rationalisieren vom Typ  und ganz allgemein, wenn der Nenner ein Binom mit mindestens einer Wurzel ist. Der Zähler und der Nenner werden mit dem konjugierten Wert des Nenners multipliziert.
und ganz allgemein, wenn der Nenner ein Binom mit mindestens einer Wurzel ist. Der Zähler und der Nenner werden mit dem konjugierten Wert des Nenners multipliziert.
Logarithmen
Der Logarithmus einer Zahl zu einer bestimmten Basis ist der Exponent, auf den die Basis erhöht werden muss, um die Zahl zu erhalten ,
,
wobei  die Basis,
die Basis,  die Zahl,
die Zahl,  der Logarithmus ist.
der Logarithmus ist.
Aus der Definition des Logarithmus können wir ableiten:
- Es gibt keinen Logarithmus einer Zahl mit einer negativen Basis.

- Den Logarithmus einer negativen Zahl gibt es nicht.

- Es gibt keinen Logarithmus von 0

- Der Logarithmus von 1 ist 0

- Der Logarithmus zur Basis
 von
von  ist 1
ist 1
- Der Logarithmus zur Basis
 einer Potenz zur Basis
einer Potenz zur Basis  ist gleich dem Exponenten
ist gleich dem Exponenten
Eigenschaften von Logarithmen
Eigenschaften
1 Der Logarithmus eines Produkts ist gleich der Summe der Logarithmen der Faktoren:
2 Der Logarithmus eines Quotienten ist gleich dem Logarithmus des Dividenden minus dem Logarithmus des Divisors: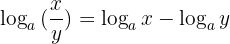
3 Der Logarithmus einer Potenz ist gleich dem Produkt aus dem Exponenten und dem Logarithmus der Basis:
4 Der Logarithmus einer Wurzel ist gleich dem Quotienten aus dem Logarithmus des Radikanden und dem Wurzelexponenten: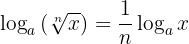
5 Änderung der Basis: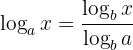
Mit KI zusammenfassen: