Kapitel
Irrationale Zahlen
Eine Zahl ist irrational, wenn sie unendlich viele nicht periodische Nachkommastellen hat und daher nicht als Bruch ausgedrückt werden kann.
Reellen Zahlen
Die aus den rationalen und irrationalen Zahlen gebildete Menge ist die Menge der reellen Zahlen, bezeichnet mit 
.
Mit reellen Zahlen können wir alle Rechenoperationen durchführen, mit Ausnahme des Radizierens geradzahliger und negativer Radikanden und der Division durch 0.
Intervalle werden durch zwei Zahlen bestimmt, die als Extremwerte bezeichnet werden. In einem Intervall gibt es alle Zahlen, die zwischen den beiden liegen, und auch die Extremwerte können enthalten sein.
Intervalle
Offenes Intervall
Die Extremwerte des Intervalls gehöhren nicht dazu
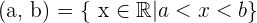
Abgeschlossenes Intervall
Die Extremwerte gehören dazu
Linksoffenes Intervall
Der rechte Extremwert des Intervalls gehört dazu, der linke Extremwert nicht
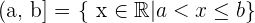
Rechtsoffenes Intervall
Der linke Extremwert des Intervalls gehört dazu, der rechte Extremwert nicht
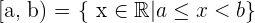
Halbgeraden
Rechtsseitige Halbgerade
1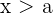 
Der linke Extremwert gehört nicht dazu
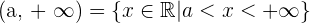
2 
Der linke Extremwert gehört dazu
Linksseitige Halbgerade
1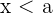 
Der rechte Extremwert gehört nicht dazu
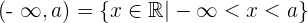
2 
Der rechte Extremwert gehört dazu
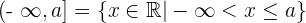
Betrag
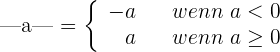
Regeln
1 
2 
3 
Distanz
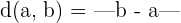
Umgebungen
Das offene Intervall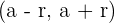 
wird Umgebung mit Mittelpunkt a und Radius 
genannt und mit 
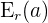oder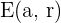 
bezeichnet.
Seitliche Umgebungen
Auf der linken Seite
Auf der rechten Seite
Eingeschränkte Umgebung
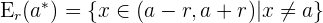
Regeln für Potenzen
1 
2 
3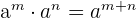 
4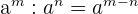 
5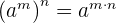 
6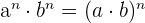 
7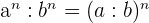 
8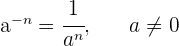 
Wurzeln
Eine Wurzel ist ein Ausdruck der Form 
, wobei 
und 
; wenn 
negativ ist, muss 
ungerade sein.
Eine Wurzel kann als eine Potenz ausgedrückt werden:
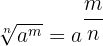
Äquivalente Wurzeln
1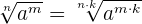
2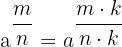
Vereinfachung von Wurzeln
Wenn es eine natürliche Zahl gibt, die den Wurzelexponenten und den Exponenten (oder die Exponenten) des Radikanden teilt, erhält man eine vereinfachte Wurzel.
Wurzeln auf einen gemeinsamen Wurzelexponenten bringen
1Wir ermitteln das kleinste gemeinsame Vielfache der Wurzelexponenten, das dann der gemeinsame Wurzelexponent ist.
2Wir dividieren den gemeinsamen Wurzelexponenten durch jeden der Wurzelexponenten und multiplizieren jedes erhaltene Ergebnis mit dem entsprechenden Exponenten.
Extrahieren von Faktoren außerhalb der Wurzel
Der Radikand wird in Faktoren zerlegt:
1Wenn ein Exponent kleiner als der Wurzelexponent ist, wird der entsprechende Faktor im Radikanden belassen.
2Wenn ein Exponent gleich dem Wurzelexponenten ist, verlässt der entsprechende Faktor den Radikanden.
3Wenn ein Exponent größer als der Wurzelexponent ist, wird der Exponent durch den Wurzelexponenten dividiert. Der erhaltene Quotient ist der Exponent des Faktors außerhalb des Radikanden und der Rest ist der Exponent des Faktors innerhalb des Radikanden.
Faktoren unter die Wurzel bringen
1 Es werden die auf den entsprechenden Wurzelexponenten angehobenen Faktoren unter die Wurzel gebracht.
Rechnen mit Wurzeln
Addition von Wurzeln
Zwei Wurzeln können nur dann addiert (oder subtrahiert) werden, wenn es sich um ähnliche Wurzeln handelt, d. h. wenn es sich um Wurzeln mit demselben Wurzelexponenten und demselben Radikanden handelt.
Produkt aus Wurzeln
1 Wurzeln mit demselben Wurzelexponenten
2 Wurzeln mit unterschiedlichem Wurzelexponenten
Zunächst müssen sie auf einen gemeinsamen Wurzelexponenten gebracht und dann multipliziert werden.
Quotient aus Wurzeln
1 Wurzeln mit demselben Wurzelexponenten
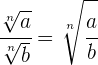
2 Wurzeln mit unterschiedlichem Wurzelexponenten
Wir bringen sie zunächst auf einen gemeinsamen Wurzelexponenten und dividieren im Anschluss.
Potenzen von Wurzeln
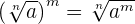
Wurzel einer Wurzel
Rationalisieren
Besteht darin, die Wurzeln aus dem Nenner zu entfernen, was Rechenoperationen wie die Addition von Brüchen erleichtert.
Wir können drei Fälle unterscheiden.
1 
Der Zähler und der Nenner werden mit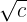 
multipliziert.
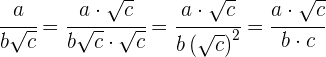
2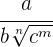 
Der Zähler und der Nenner werden mit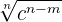 
multipliziert.
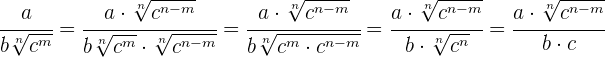
3 
, und ganz allgemein, wenn der Nenner ein Binom mit mindestens einer Wurzel ist.
Der Zähler und der Nenner werden mit der Konjugation des Nenners multipliziert.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
