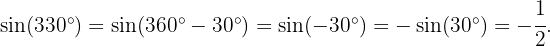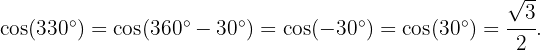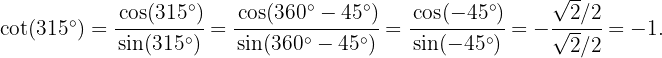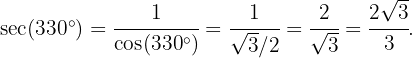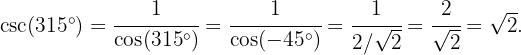Willkommen auf unserer Seite mit Übungen zur Trigonometrie! Hier findest du eine Vielzahl von Aufgaben, die von den Grundlagen bis zu den fortgeschrittensten Konzepten in diesem faszinierenden Bereich der Mathematik reichen.
Die Trigonometrie ist ein Teilgebiet der Mathematik, das die Beziehungen zwischen den Winkeln und Seiten von Dreiecken untersucht. Diese Disziplin, die ihre Wurzeln in der Astronomie und Navigation hat, findet in einer Vielzahl von Bereichen Anwendung, von der Physik über das Ingenieurwesen bis hin zur Informatik und darüber hinaus.
Unsere Seite soll dir helfen, deine Trigonometriekenntnisse zu verbessern. Jede Übung ist so konzipiert, dass sie dein Verständnis herausfordert und deine Problemlösungskompetenz verbessert.
Und denk daran: Übung macht den Meister. Also, nur zu! Entdecke mit diesen Übungen die Schönheit und Nützlichkeit der Trigonometrie.
Gegeben ist 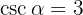 . Berechne die restlichen trigonometrischen Verhältnisse.
. Berechne die restlichen trigonometrischen Verhältnisse.
Der Kosekans ist in zwei Quadranten positiv, die Werte von  y
y  sind in beiden Quadranten gleich, der Unterschied zwischen den beiden Fällen sind die Vorzeichen einiger trigonometrischer Verhältnisse. Wir beginnen also mit der Berechnung der Werte von
sind in beiden Quadranten gleich, der Unterschied zwischen den beiden Fällen sind die Vorzeichen einiger trigonometrischer Verhältnisse. Wir beginnen also mit der Berechnung der Werte von  und
und  . Die Definition des Kosekans ist
. Die Definition des Kosekans ist  , weshalb
, weshalb 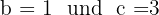 . Nun berechnen wir den Wert von
. Nun berechnen wir den Wert von  mithilfe des Satzes des Pythagoras:
mithilfe des Satzes des Pythagoras: 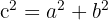

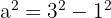
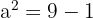
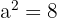
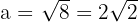
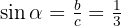
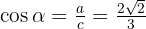

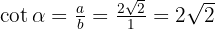
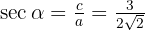
 in diesem Quadranten negativ ist:
in diesem Quadranten negativ ist: 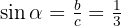
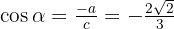

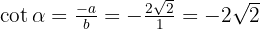

Berechne die Verhältnisse der folgenden Winkel:
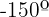
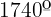
Denke daran, dass je nach Funktion negative Winkel die Funktion negativ machen können oder nicht. Bei Winkeln größer als 90º versuchen wir außerdem, den Winkel wie folgt auszudrücken: 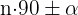 , wobei, wenn
, wobei, wenn  gerade ist, entspricht dies der Funktion von
gerade ist, entspricht dies der Funktion von 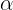 . Das heißt,
. Das heißt, 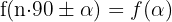 , wobei
, wobei  die trigonometrischen Verhältnisse darstellt. Es ist auch wichtig, daran zu denken, dass Funktionen unterschiedliche Vorzeichen haben, je nachdem, in welchem Quadranten sie sich befinden.
die trigonometrischen Verhältnisse darstellt. Es ist auch wichtig, daran zu denken, dass Funktionen unterschiedliche Vorzeichen haben, je nachdem, in welchem Quadranten sie sich befinden.
a 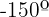
 . Wir befinden uns also im 2. Quadranten und müssen uns daher das Vorzeichen jeder Funktion ansehen:
. Wir befinden uns also im 2. Quadranten und müssen uns daher das Vorzeichen jeder Funktion ansehen: 
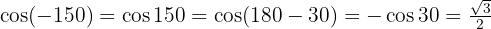
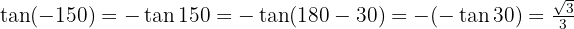
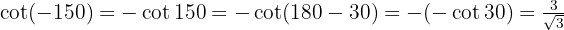
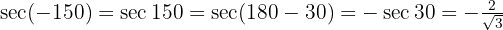

b 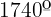
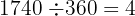 und wir haben einen Rest von
und wir haben einen Rest von  , welcher äquivalent ist. Also berechnen wir die trigonometrischen Funktionen für den Winkel
, welcher äquivalent ist. Also berechnen wir die trigonometrischen Funktionen für den Winkel  .
. 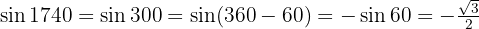
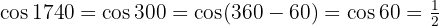
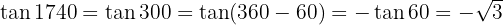
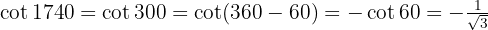
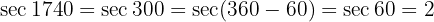
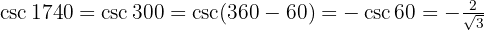
Vereinfache die Brüche:

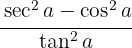
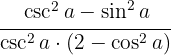
Um die Brüche zu vereinfachen, müssen wir uns sowohl an die trigonometrischen Funktionen und ihre Definitionen als auch an einige trigonometrische Identitäten erinnern.
 Wir beginnen mit der direkten Anwendung der entsprechenden trigonometrischen Identitäten und ändern dann die Definition von Sekans und Kosekans,
Wir beginnen mit der direkten Anwendung der entsprechenden trigonometrischen Identitäten und ändern dann die Definition von Sekans und Kosekans,  , um schließlich die Brüche zu dividieren und die Definition des Tangens zu ermitteln.
, um schließlich die Brüche zu dividieren und die Definition des Tangens zu ermitteln. 
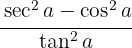 Wir nutzen die Definition des Sekans, subtrahieren und dividieren die Brüche,
Wir nutzen die Definition des Sekans, subtrahieren und dividieren die Brüche, 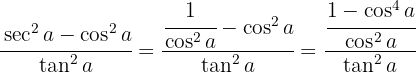 Wir wandeln die Differenz der Quadrate in konjugierte Binome um und ändern die Definition des Tangens.
Wir wandeln die Differenz der Quadrate in konjugierte Binome um und ändern die Definition des Tangens. 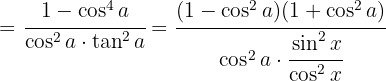 Wir streichen die Kosinusse und wenden an:
Wir streichen die Kosinusse und wenden an: 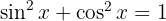

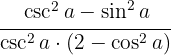 Wir trennen die Brüche und vereinfachen,
Wir trennen die Brüche und vereinfachen, 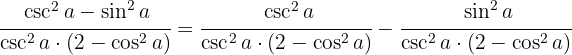 Wir bringen die Subtraktion wieder zusammen und teilen die Zahl 2, um die Identität
Wir bringen die Subtraktion wieder zusammen und teilen die Zahl 2, um die Identität 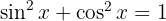
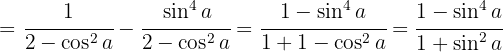 nutzen zu können. Wir wandeln die Differenz der Quadrate in konjugierte Binome um und wenden die Identität wieder an:
nutzen zu können. Wir wandeln die Differenz der Quadrate in konjugierte Binome um und wenden die Identität wieder an: 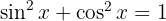

Berechne die Länge der Seite und des Apothemas eines regelmäßigen Achtecks, das in einen Kreis mit dem Radius 49 cm eingeschrieben ist.
Wir beginnen damit, den Wert des Winkels zu berechnen:
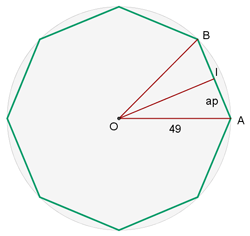
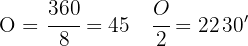 Wir teilen den Winkel in zwei Hälften, so dass wir ein rechtwinkliges Dreieck bilden und die trigonometrischen Funktionen anwenden können. Um den Wert der Seite zu ermitteln, verwenden wir die Sinusfunktion.
Wir teilen den Winkel in zwei Hälften, so dass wir ein rechtwinkliges Dreieck bilden und die trigonometrischen Funktionen anwenden können. Um den Wert der Seite zu ermitteln, verwenden wir die Sinusfunktion. 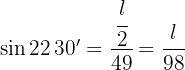 Wir berechnen den Wert von l und erhalten:
Wir berechnen den Wert von l und erhalten: 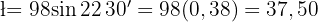 cm Um den Wert des Apothemas zu berechnen, wenden wir die Kosinusfunktion an.
cm Um den Wert des Apothemas zu berechnen, wenden wir die Kosinusfunktion an. 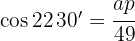 Wir ermitteln das Apothema
Wir ermitteln das Apothema 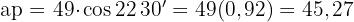 cm
cmDrei Dörfer A, B und C sind durch Straßen miteinander verbunden. Die Entfernung von A nach C beträgt 6 km und von B nach C 9 km. Der Winkel, den diese Straßen bilden, beträgt 120°. Wie weit sind A und B voneinander entfernt?
Um den Wert der Strecke zwischen A und B zu ermitteln, ist es am einfachsten, den Kosinussatz anzuwenden,
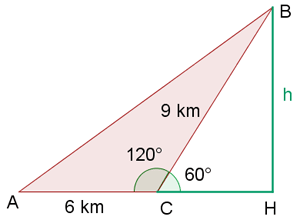
Wir beginnen mit der direkten Anwendung des Kosinussatzes, d. h: 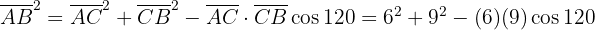

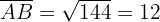 cm
cm
Löse die folgende trigonometrische Gleichung: 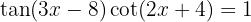
Zunächst verwenden wir die Definition von Tangens und Kotangens in Bezug auf die Sinus- und Kosinusfunktionen: 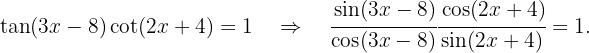 Wenn wir die Nenner entfernen und den Term der rechten Seite subtrahieren, erhalten wir
Wenn wir die Nenner entfernen und den Term der rechten Seite subtrahieren, erhalten wir 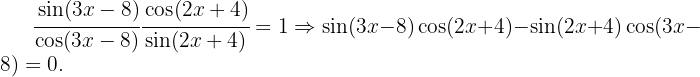 Nun verwenden wir die Formel für die Subtraktion von Winkeln der Sinusfunktion
Nun verwenden wir die Formel für die Subtraktion von Winkeln der Sinusfunktion 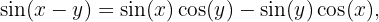 um zu erhalten, dass
um zu erhalten, dass 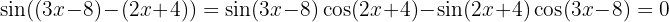 Wir haben also
Wir haben also 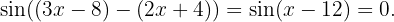 Das Problem ist also die Lösung der Gleichung
Das Problem ist also die Lösung der Gleichung 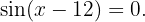 Denk daran, dass sich die Sinusfunktion aufhebt, wenn ihr Argument ein ganzzahliges Vielfaches von
Denk daran, dass sich die Sinusfunktion aufhebt, wenn ihr Argument ein ganzzahliges Vielfaches von  ist. Somit erhalten wir
ist. Somit erhalten wir 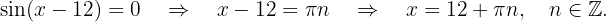 Die Lösung ist
Die Lösung ist
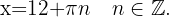
Ermittle folgende Werte
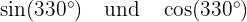
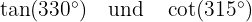
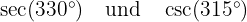
Wie in Aufgabe 2 verwenden wir wieder das Ergebnis, das uns sagt, dass  wobei
wobei  eine gerade Zahl ist und
eine gerade Zahl ist und  eine trigonometrische Funktion darstellt.
eine trigonometrische Funktion darstellt.
a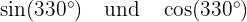
 und erhalten
und erhalten b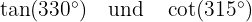
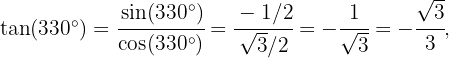 wobei wir den ersten Abschnitt verwendet haben, um das Ergebnis zu erhalten.
wobei wir den ersten Abschnitt verwendet haben, um das Ergebnis zu erhalten.
c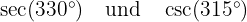
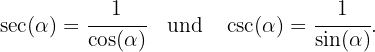 Somit:
Somit: Gegeben ist 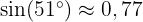 . Berechne den Wert von
. Berechne den Wert von  in der folgenden Abbildung
in der folgenden Abbildung
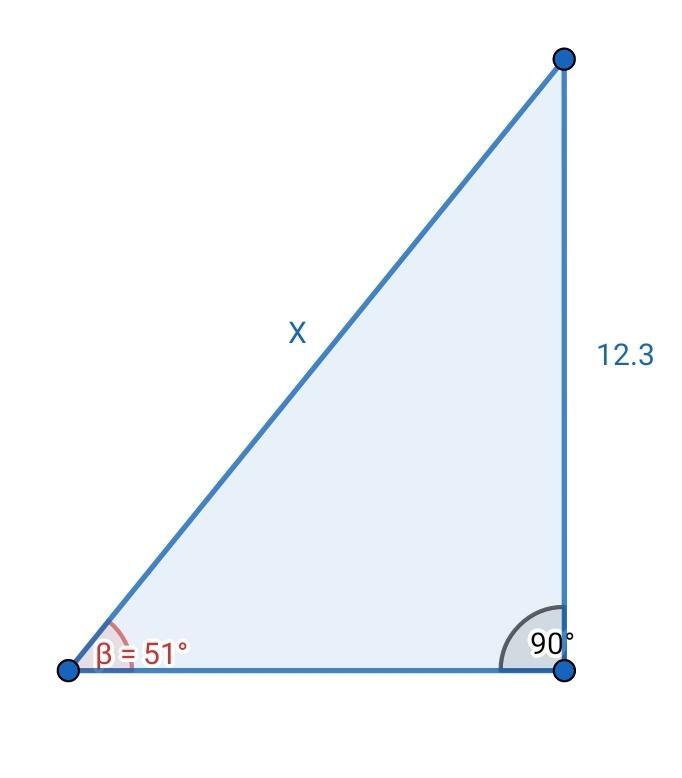
Der Wert von  stellt die Hypotenuse des rechtwinkligen Dreiecks dar. Wir haben Informationen zum Winkel und zum gegenüberliegenden Schenkel des Winkels. Da wir also die Hypotenuse ermitteln wollen, verwenden wir die Sinusfunktion:
stellt die Hypotenuse des rechtwinkligen Dreiecks dar. Wir haben Informationen zum Winkel und zum gegenüberliegenden Schenkel des Winkels. Da wir also die Hypotenuse ermitteln wollen, verwenden wir die Sinusfunktion: 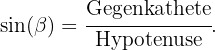
Wir haben also 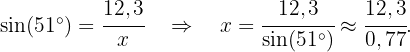
Und schließlich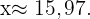
Beweise die folgenden trigonometrischen Identitäten
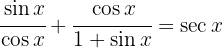
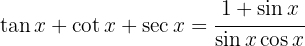
a 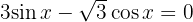 auf dem Intervall
auf dem Intervall  Es gilt, dass00
Es gilt, dass00 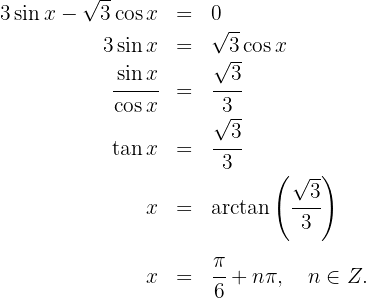 Somit ist
Somit ist 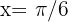 die einzige Lösung auf dem Intervall
die einzige Lösung auf dem Intervall 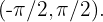
b 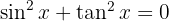 auf dem Intervall
auf dem Intervall 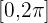
Beachte, dass 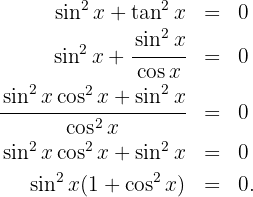 Dies bedeutet, dass
Dies bedeutet, dass 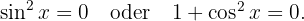
- Wenn
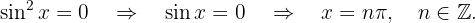
- Wenn
 , gibt es keine reellen Lösungen.
, gibt es keine reellen Lösungen.
Die Lösung ist also  Auf dem Intervall
Auf dem Intervall 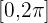 sind die Lösungen
sind die Lösungen 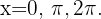
Mit KI zusammenfassen: