In der Geometrie und Trigonometrie spielen Winkel eine grundlegende Rolle beim Messen und Verstehen der räumlichen Beziehungen zwischen Objekten. In dieser Übung werden wir Winkel unter Verwendung des Sexagesimalsystems untersuchen, das eines der am häufigsten verwendeten Systeme zur Messung von Winkeln ist.
Im Sexagesimalsystem wird ein Winkel in Grad, Minuten und Sekunden unterteilt. Ein Grad ist in 60 Minuten unterteilt, und jede Minute ist wiederum in 60 Sekunden unterteilt. Daher kann ein Winkel von 1 Grad als 1° ausgedrückt werden, 1 Grad und 30 Minuten als 1°30', und so weiter. Wir üben das Umrechnen zwischen Grad, Minuten und Sekunden sowie das Addieren, Subtrahieren und Multiplizieren von Winkeln im Sexagesimalsystem.
Und nun zur Praxis!
Addiere wie folgt. Denke daran, dass  und
und 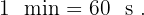
a
b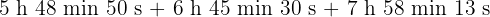
c
a
Wir addieren die Werte, deren Einheiten gleich sind und dividieren die Minuten und Sekunden durch 60.

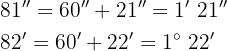
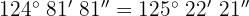
b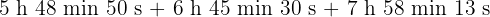
Wir addieren die Werte, deren Einheiten gleich sind und dividieren die Minuten und Sekunden durch 60.

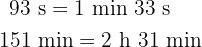
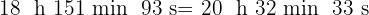
c
Wir addieren die Werte, deren Einheiten gleich sind und dividieren die Minuten und Sekunden durch 60.

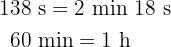
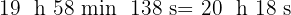
Denke daran, dass  und
und 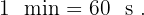
a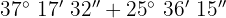
b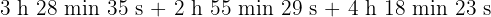
c
a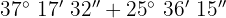
Wir addieren die Werte, deren Einheiten gleich sind und wenn die Minuten und Sekunden größer als 60 sind dividieren wir sie durch 60. In diesem Fall trifft das jedoch nicht zu und wir erhalten

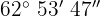
b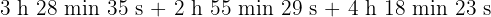
Wir addieren die Werte, deren Einheiten gleich sind und dividieren die Minuten und Sekunden durch 60.

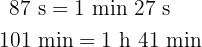
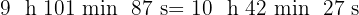
c
Wir addieren die Werte, deren Einheiten gleich sind und dividieren die Minuten und Sekunden durch 60.

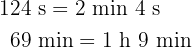
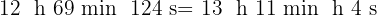
Denke daran, dass  und
und 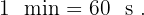
a
b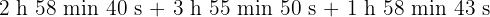
c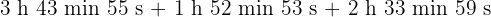
a
Wir addieren die Werte, deren Einheiten gleich sind und dividieren die Minuten und Sekunden durch 60.
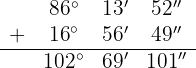
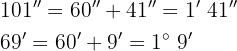

b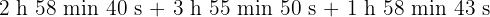
Wir addieren die Werte, deren Einheiten gleich sind und dividieren die Minuten und Sekunden durch 60.

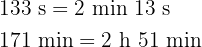
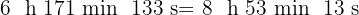
c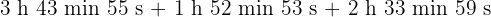
Wir addieren die Werte, deren Einheiten gleich sind und dividieren die Minuten und Sekunden durch 60.

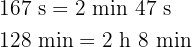

Multipliziere wie folgt:
a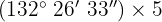
b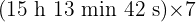
c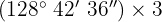
a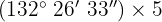
Wir multiplizieren Einheit für Einheit und dividieren die Minuten und Sekunden durch 60.
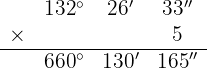
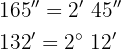
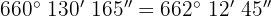
b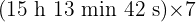
Wir multiplizieren Einheit für Einheit und dividieren die Minuten und Sekunden durch 60.
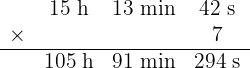
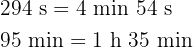
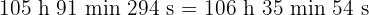
c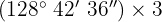
Wir multiplizieren Einheit für Einheit und dividieren die Minuten und Sekunden durch 60.
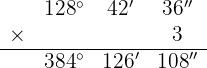
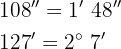
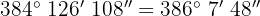
Multipliziere wie folgt:
a
b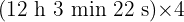
c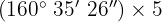
a
Wir multiplizieren Einheit für Einheit und dividieren die Minuten und Sekunden durch 60.
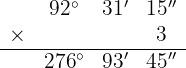
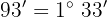
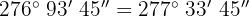
b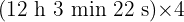
Wir multiplizieren Einheit für Einheit und dividieren die Minuten und Sekunden durch 60.

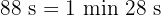

c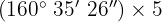
Wir multiplizieren Einheit für Einheit und dividieren die Minuten und Sekunden durch 60.
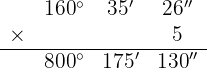
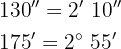
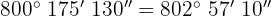
Dividiere wie folgt
a
b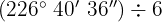
a
Wir dividieren Einheit für Einheit. Der Quotient wird in eine Untereinheit umgewandelt, addiert und anschließend dividiert.
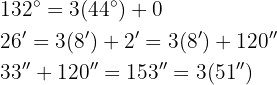
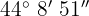
b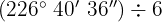
Wir dividieren Einheit für Einheit. Der Quotient wird in eine Untereinheit umgewandelt, addiert und anschließend dividiert.
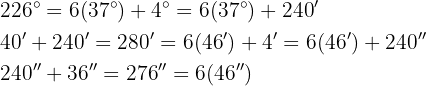

Dividiere wie folgt
a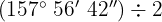
b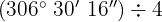
a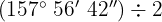
Wir dividieren Einheit für Einheit. Der Quotient wird in eine Untereinheit umgewandelt, addiert und anschließend dividiert.
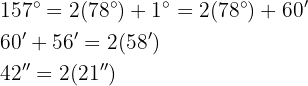

b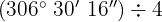
Wir dividieren Einheit für Einheit. Der Quotient wird in eine Untereinheit umgewandelt, addiert und anschließend dividiert.
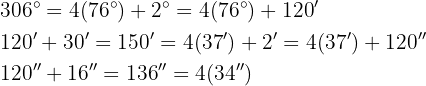

Berechne die Komplementär- und Ergänzungswinkel von 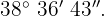
1Berechnung des Komplementärwinkels
Da ein Winkel und sein Komplementärwinkel 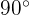 ergeben müssen, wird die Differenz berechnet, indem in eine Untereinheit umgerechnet wird:
ergeben müssen, wird die Differenz berechnet, indem in eine Untereinheit umgerechnet wird: 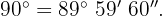

2Berechnung des Ergänzungswinkels
Da ein Winkel und sein Ergänzungswinkel 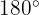 ergeben müssen, wird die Differenz berechnet, indem in eine Untereinheit umgerechnet wird:
ergeben müssen, wird die Differenz berechnet, indem in eine Untereinheit umgerechnet wird: 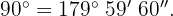

Berechne die Komplementär- und Ergänzungswinkel von 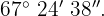
1Berechnung des Komplementärwinkels
Da ein Winkel und sein Komplementärwinkel 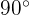 ergeben müssen, wird die Differenz berechnet, indem in eine Untereinheit umgerechnet wird:
ergeben müssen, wird die Differenz berechnet, indem in eine Untereinheit umgerechnet wird: 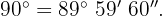
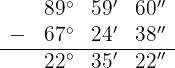
2Berechnung des Ergänzungswinkels
Da ein Winkel und sein Ergänzungswinkel 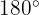 ergeben müssen, wird die Differenz berechnet, indem in eine Untereinheit umgerechnet wird:
ergeben müssen, wird die Differenz berechnet, indem in eine Untereinheit umgerechnet wird: 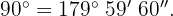

Berechne die Komplementär- und Ergänzungswinkel von 
1Berechnung des Komplementärwinkels
Da ein Winkel und sein Komplementärwinkel 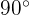 ergeben müssen, wird die Differenz berechnet, indem in eine Untereinheit umgerechnet wird:
ergeben müssen, wird die Differenz berechnet, indem in eine Untereinheit umgerechnet wird: 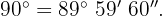

2Berechnung des Ergänzungswinkels
Da ein Winkel und sein Ergänzungswinkel 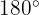 ergeben müssen, wird die Differenz berechnet, indem in eine Untereinheit umgerechnet wird:
ergeben müssen, wird die Differenz berechnet, indem in eine Untereinheit umgerechnet wird: 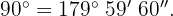

Mit KI zusammenfassen:


