

Für die linke Seite der Gleichung wenden wir die Definitionen von Tangens und Kotangens an
Wir wissen, dass  ist und wenden die Definitionen von Sekans und Kosekans an. Wir erhalten somit
ist und wenden die Definitionen von Sekans und Kosekans an. Wir erhalten somit

Dies ist schließlich unser gesuchtes Ergebnis.

 Zunächst multiplizieren wir die Klammer aus
Zunächst multiplizieren wir die Klammer aus

Wir klammern  aus beiden Summanden aus, nutzen
aus beiden Summanden aus, nutzen  und wenden die Definitionen von Kosekans und Kotangens an
und wenden die Definitionen von Kosekans und Kotangens an


 Wir sehen uns zunächst die rechte Seite an und klammern
Wir sehen uns zunächst die rechte Seite an und klammern  aus beiden Summanden aus
aus beiden Summanden aus

Wir nutzen  und wenden die Definition des Sekans an
und wenden die Definition des Sekans an

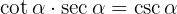
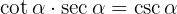 Wir wenden die Definitionen von Kotangens und Sekans an
Wir wenden die Definitionen von Kotangens und Sekans an
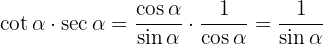
Wir kürzen den Faktor 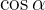 und wenden die Definition des Kosekans an
und wenden die Definition des Kosekans an
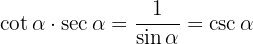
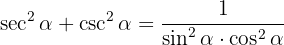
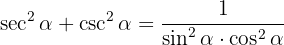 Wir wenden die Definitionen von Sekans und Kosekans an und addieren die Brüche
Wir wenden die Definitionen von Sekans und Kosekans an und addieren die Brüche
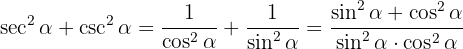
Schließlich nutzen wir die Identität  und erhalten das gewünschte Ergebnis
und erhalten das gewünschte Ergebnis
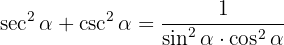
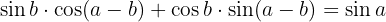
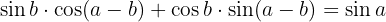 Wir stellen zunächst fest, dass
Wir stellen zunächst fest, dass
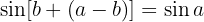
Die Formel für den Sinus der Summe lautet
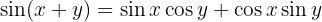
Hierdurch erhalten wir sofort die gewünschte Identität
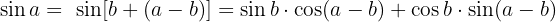
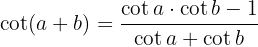
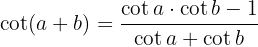 Die Definition des Kotangens besagt, dass
Die Definition des Kotangens besagt, dass

Wir verwenden die Formel für den Tangens der Summe und vereinfachen

Wir dividieren den Zähler und den Nenner durch  , um dann mit Hilfe des Kotangens den Ausdruck zu vereinfachen
, um dann mit Hilfe des Kotangens den Ausdruck zu vereinfachen
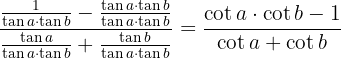
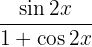
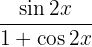
Wir wenden die Formel für den Sinus des Doppelwinkels an
Und da  , gilt
, gilt 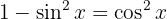
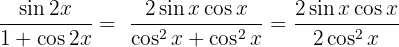
Wir vereinfachen und wenden die Definition des Tangens an
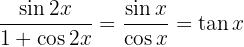
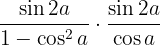
latex]\displaystyle \frac{\sin 2a}{1-\cos^2a}\cdot \frac{\sin 2a}{\cos a}[/latex]
Wir nutzen, dass  ist und wenden die Formel für den Sinus des Doppelwinkels an. Im Anschluss multiplizieren wir die Brüche
ist und wenden die Formel für den Sinus des Doppelwinkels an. Im Anschluss multiplizieren wir die Brüche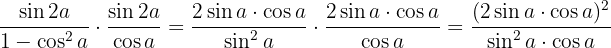
wir vereinfachen
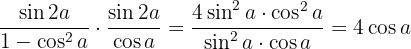
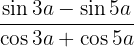
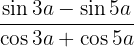 Wir wenden die Formeln an, mit denen aus einer Summe trigonometrischer Funktionen ein Produkt wird
Wir wenden die Formeln an, mit denen aus einer Summe trigonometrischer Funktionen ein Produkt wird

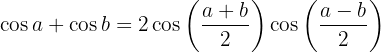
Somit
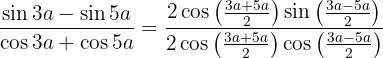
Wir vereinfachen und wenden die Definition des Tangens an. Außerdem ist der Tangens eine ungerade Funktion, so dass 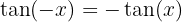
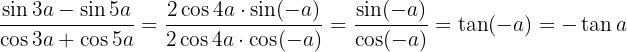
Mit KI zusammenfassen:


