Kapitel

Entfernung zwischen einem zugänglichen Punkt und einem unzugänglichen Punkt
Wenn man einen unzugänglichen Punkt  hat und seine Entfernung zu einem zugänglichen Punkt
hat und seine Entfernung zu einem zugänglichen Punkt  messen will, misst man die Entfernung von
messen will, misst man die Entfernung von  zu einem zweiten zugänglichen Punkt
zu einem zweiten zugänglichen Punkt  so, dass man ein Dreieck mit den Eckpunkten
so, dass man ein Dreieck mit den Eckpunkten  erhält.
erhält.

Mithilfe eines Theodoliten werden die den bekannten Eckpunkten entsprechenden Winkel gemessen.
Wir wenden den Sinussatz an und erhalten die Entfernung zwischen den Punkten  und
und  .
.
Beispiel: Ermittle die Entfernung zwischen zwei Punkten  und
und  , wenn bekannt ist, dass die Entfernung von
, wenn bekannt ist, dass die Entfernung von  zu einem Punkt
zu einem Punkt 
 beträgt und mit Hilfe eines Theodoliten ermittelt wurde, dass
beträgt und mit Hilfe eines Theodoliten ermittelt wurde, dass 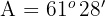 und
und  .
.
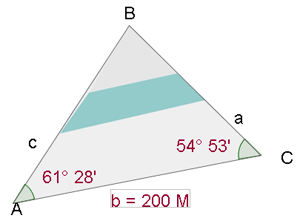
1Wir berechnen das Maß des Winkels  und verwenden dazu das Ergebnis, das besagt, dass die Summe der Innenwinkel eines Dreiecks gleich
und verwenden dazu das Ergebnis, das besagt, dass die Summe der Innenwinkel eines Dreiecks gleich  ist.
ist.
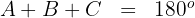
2Wir setzen die bekannten Werte der Winkel  ,
,  ein und lösen nach
ein und lösen nach  auf.
auf.
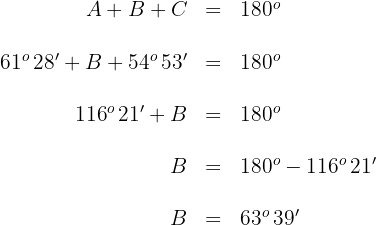
3Wir wenden den Sinussatz für 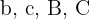 an
an
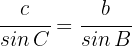
4Wir setzen die bekannten Werte ein und lösen nach  auf
auf

Somit ist die gesuchte Entfernung 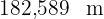
Aufgaben mit Lösungen
Ermittle die Entfernung zwischen zwei Punkten  und
und  , die durch einen Fluss getrennt sind, wenn bekannt ist, dass die Entfernung von
, die durch einen Fluss getrennt sind, wenn bekannt ist, dass die Entfernung von  zu einem Punkt
zu einem Punkt 
 beträgt und mit Hilfe eines Theodoliten ermittelt wurde, dass
beträgt und mit Hilfe eines Theodoliten ermittelt wurde, dass  und
und 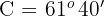 .
.
1Wir stellen grafisch dar:
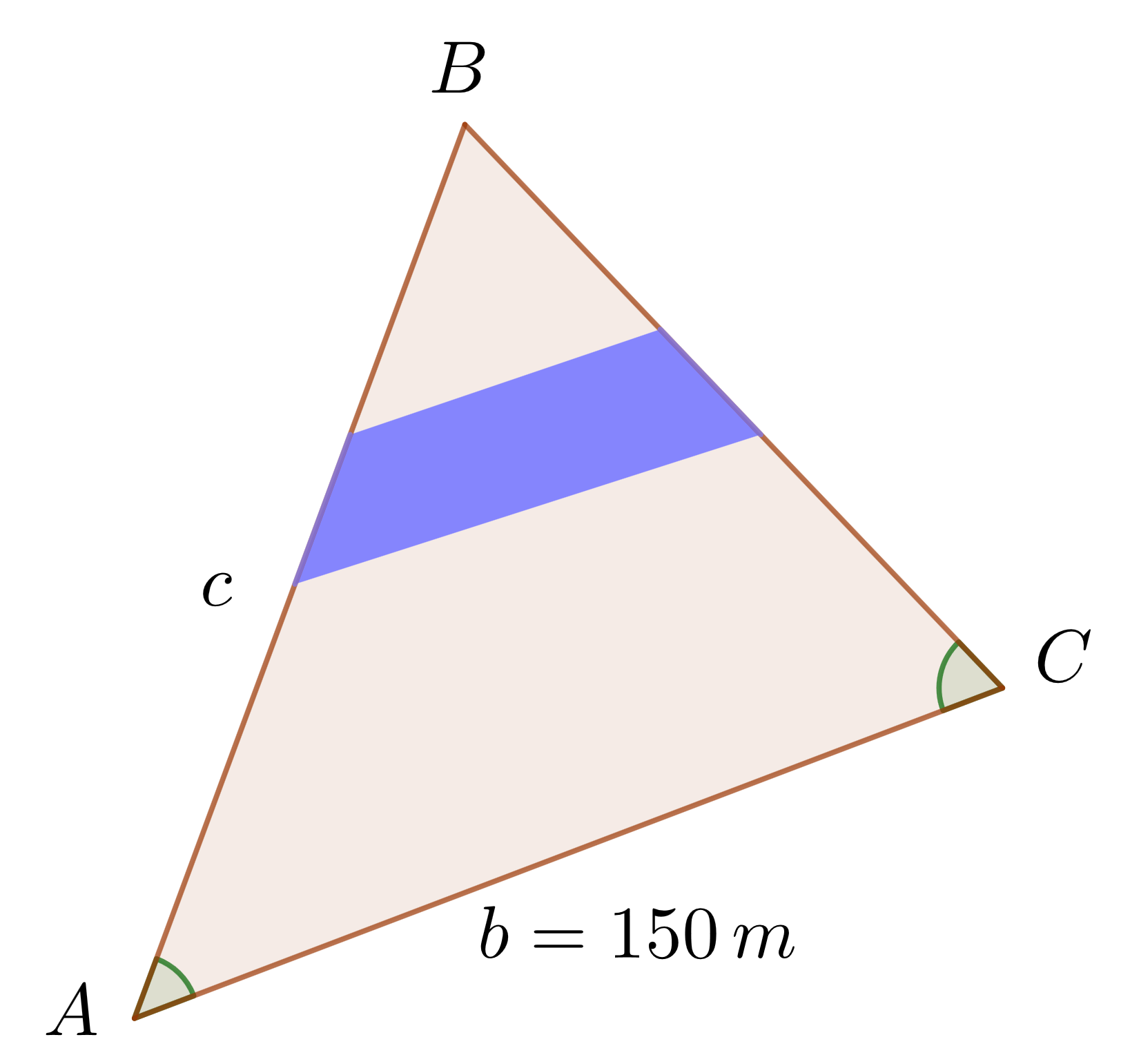
2Wir berechnen das Maß des Winkels  und verwenden dazu das Ergebnis, das besagt, dass die Summe der Innenwinkel eines Dreiecks gleich
und verwenden dazu das Ergebnis, das besagt, dass die Summe der Innenwinkel eines Dreiecks gleich  ist.
ist.

3Wir setzen die bekannten Werte für die Winkel  ,
,  ein und lösen nach
ein und lösen nach 

4Wir wenden den Sinussatz für 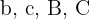 an
an
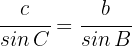
5Wir setzen die uns bekannten Werte ein und lösen nach 
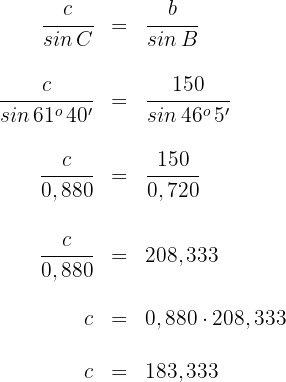
Somit ist die gesuchte Entfernung 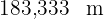
Ein Mann am Strand möchte wissen, wie weit eine Insel entfernt ist. Er betrachtet also zwei Punkte am Strand, die  voneinander entfernt sind, und ermittelt mit Hilfe eines Theodoliten die Winkel für die Punkte am Strand. Diese sind
voneinander entfernt sind, und ermittelt mit Hilfe eines Theodoliten die Winkel für die Punkte am Strand. Diese sind  und
und 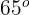 . Wie weit ist die Insel vom ersten Punkt entfernt?
. Wie weit ist die Insel vom ersten Punkt entfernt?
1Wir stellen grafisch dar

2Wir berechnen das Maß des Winkels  . Dazu verwenden wir das Ergebnis, das uns sagt, dass die Summe der Innenwinkel eines Dreiecks gleich
. Dazu verwenden wir das Ergebnis, das uns sagt, dass die Summe der Innenwinkel eines Dreiecks gleich  ist.
ist.

3Wir setzen die bekannten Werte für die Winkel  ,
,  ein und lösen nach
ein und lösen nach 
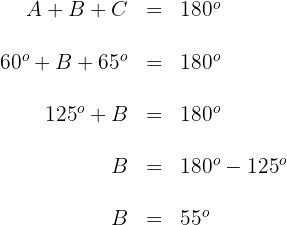
4Wir wenden den Sinussatz für 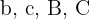 an
an
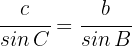
5Wir setzen die uns bekannten Werte ein und lösen nach 
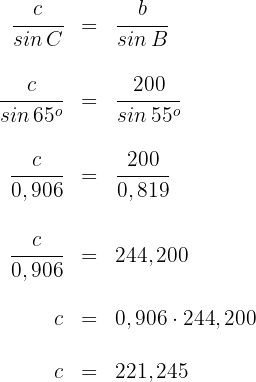
Somit ist die gesuchte Entfernung 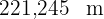
Ein Kind lässt einen Drachen steigen und sein Vater befindet sich in  Entfernung. Wenn die Winkel der Höhe des Kindes und des Vaters in Bezug auf den Drachen jeweils
Entfernung. Wenn die Winkel der Höhe des Kindes und des Vaters in Bezug auf den Drachen jeweils 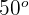 und
und  sind, wie groß ist dann die Entfernung zwischen dem Vater und dem Drachen?
sind, wie groß ist dann die Entfernung zwischen dem Vater und dem Drachen?
1Wir stellen grafisch dar
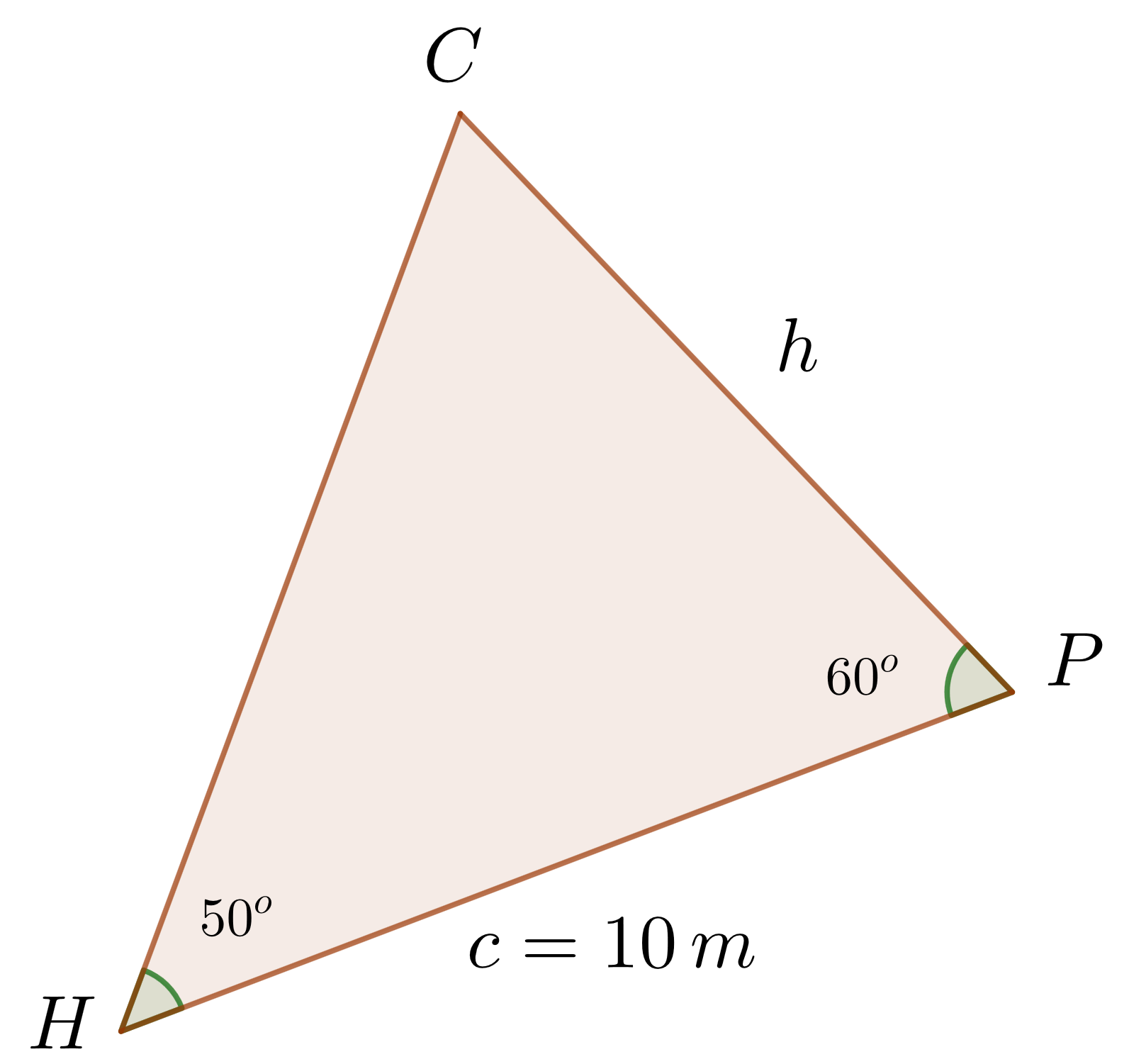
2Wir berechnen das Maß des Winkels  . Dazu verwenden wir das Ergebnis, das uns sagt, dass die Summe der Innenwinkel eines Dreiecks gleich
. Dazu verwenden wir das Ergebnis, das uns sagt, dass die Summe der Innenwinkel eines Dreiecks gleich  ist.
ist.

3Wir setzen die bekannten Werte für die Winkel 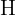 ,
,  ein und lösen nach
ein und lösen nach 
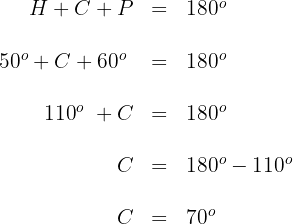
4Wir wenden den Sinussatz für 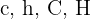 an
an
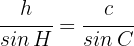
5Wir setzen die uns bekannten Werte ein und lösen nach 
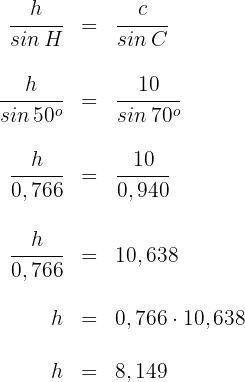
Somit ist die gesuchte Entfernung 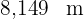
Zwei Boote sind 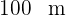 voneinander entfernt und blicken beide auf einen Steg am Strand. Wenn die Winkel der Boote zum Steg
voneinander entfernt und blicken beide auf einen Steg am Strand. Wenn die Winkel der Boote zum Steg 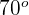 und
und 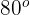 sind, bestimme die Entfernung des ersten Bootes zum Steg.
sind, bestimme die Entfernung des ersten Bootes zum Steg.
1Wir stellen grafisch dar

2Wir berechnen das Maß des Winkels  . Dazu verwenden wir das Ergebnis, das uns sagt, dass die Summe der Innenwinkel eines Dreiecks gleich
. Dazu verwenden wir das Ergebnis, das uns sagt, dass die Summe der Innenwinkel eines Dreiecks gleich  ist.
ist.

3Wir setzen die bekannten Werte für die Winkel 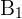 ,
,  ein und lösen nach
ein und lösen nach  .
.

4Wir wenden den Sinussatz für  an
an
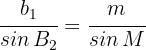
5Wir setzen die uns bekannten Werte ein und lösen nach 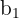
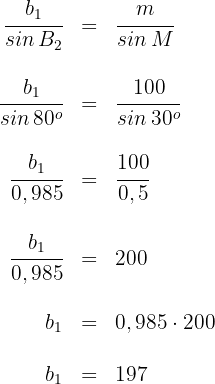
Somit ist die gesuchte Entfernung 
Ermittle die Entfernung zwischen zwei Punkten  und
und  , wenn bekannt ist, dass die Entfernung von
, wenn bekannt ist, dass die Entfernung von  zu einem Punkt
zu einem Punkt 
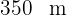 beträgt und mit Hilfe eines Theodoliten ermittelt wurde, dass
beträgt und mit Hilfe eines Theodoliten ermittelt wurde, dass  und
und  .
.
1Wir stellen grafisch dar
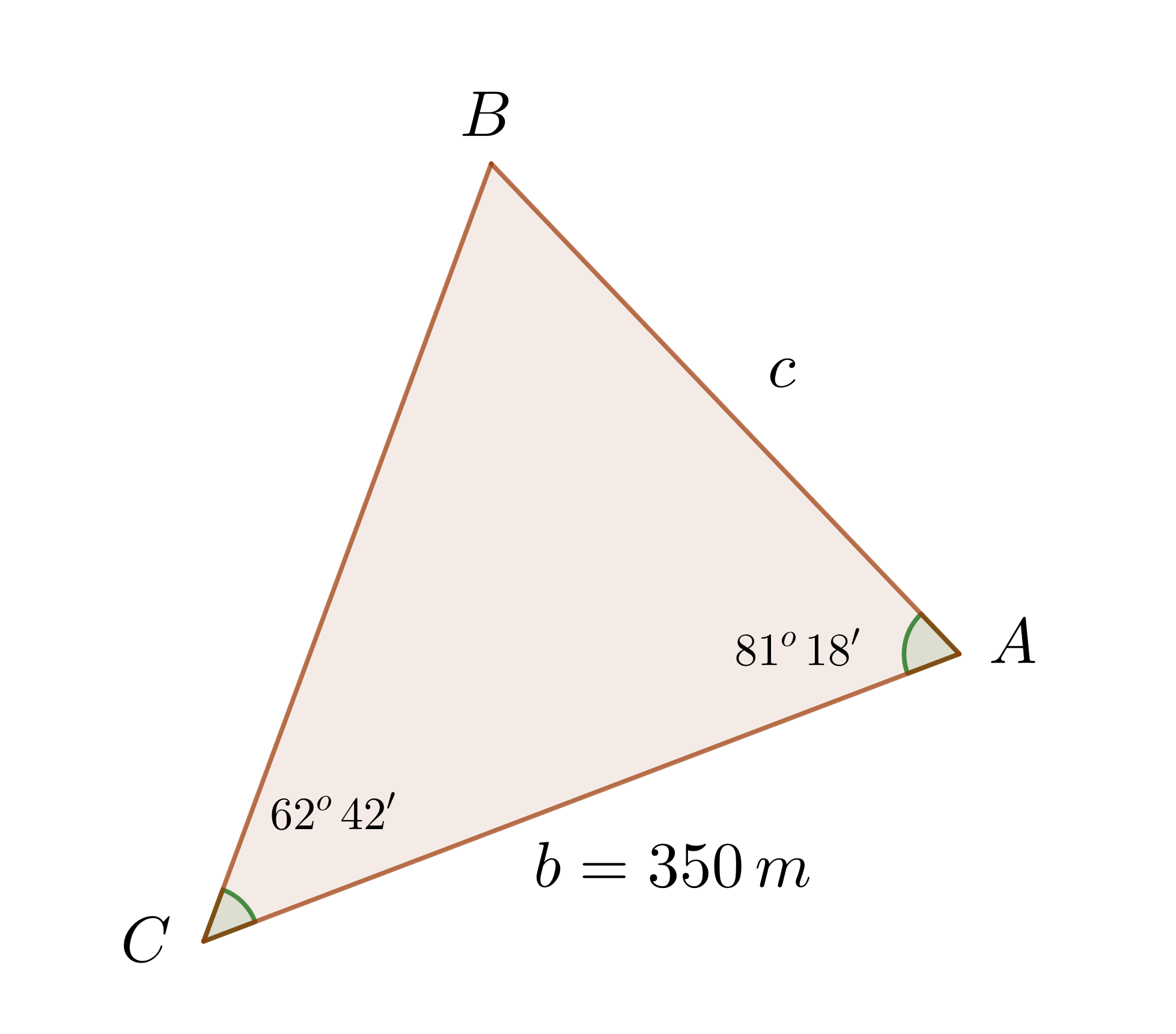
2Wir berechnen das Maß des Winkels  . Dazu verwenden wir das Ergebnis, das uns sagt, dass die Summe der Innenwinkel eines Dreiecks gleich
. Dazu verwenden wir das Ergebnis, das uns sagt, dass die Summe der Innenwinkel eines Dreiecks gleich  ist.
ist.

3Wir setzen die bekannten Werte für die Winkel  ,
,  ein und lösen nach
ein und lösen nach  .
.
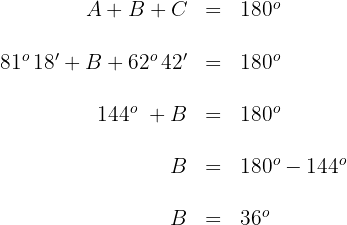
4Wir wenden den Sinussatz für 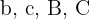 an
an
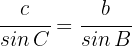
5Wir setzen die uns bekannten Werte ein und lösen nach 
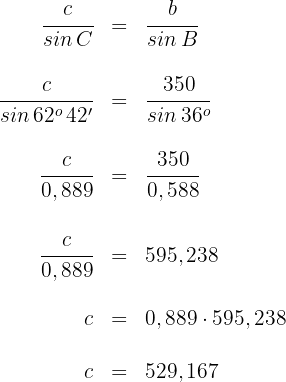
Somit ist die gesuchte Entfernung 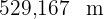
Mit KI zusammenfassen:












