Das allgemeine Glied einer Zahlenfolge ist ein Kriterium, mit dem wir jeden beliebigen Term der Zahlenfolge bestimmen können. Wir schreiben 
.
1 Überprüfe, ob die Zahlenfolge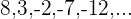 
eine arithmetische Folge ist.
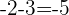
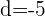
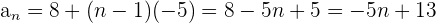
2 Überprüfe, ob die Zahlenfolge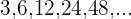 
eine geometrische Zahlenfolge ist.
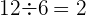
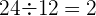
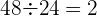
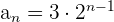
3 Überprüfe, ob die Glieder der Zahlenfolge 
Quadratzahlen sind.
Wir stellen fest, dass die Basen eine arithmetische Folge sind, wobei 
und der Exponent konstant ist
Das allgemeine Glied ist also:
Wir können auch Zahlenfolgen bestimmen, deren Glieder Zahlen sind, die nahe an Quadratzahlen liegen
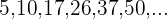
Wir ermitteln das allgemeine Glied wie im vorherigen Beispiel und addieren 1.
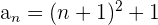
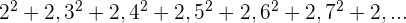
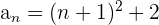
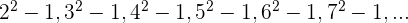
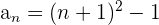
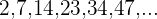
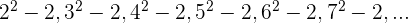
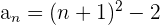
4 Wenn die Glieder der Zahlenfolge nacheinander das Vorzeichen wechseln.
Wenn die ungeraden Glieder negativ sind und die geraden positiv: Wir multiplizieren mal 
.
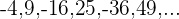
Wenn die ungeraden Glieder positiv sind und die geraden negativ: Wir multiplizieren mal 
.
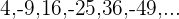
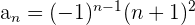
5 Wenn die Glieder Brüche sind
Das allgemeine Glied des Zählers und des Nenners wird separat berechnet.
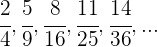
Wir haben zwei Zahlenfolgen:
Die erste Zahlenfolge ist eine arithmetische Folge mit 
, die zweite ist eine Folge von Quadratzahlen
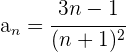
Mit KI zusammenfassen:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
