Um den Sinus, den Kosinus und den Tangens des Doppelten eines bestimmten Winkels zu bestimmen, wenden wir die Formeln für den Doppelwinkel an. Dies kann für jeden beliebigen Winkel angewendet werden, vorausgesetzt, sein Wert ist für die drei oben genannten trigonometrischen Funktionen bekannt.
Sinus des Doppelwinkels
Die Formel zur Berechnung des Sinus eines Doppelwinkels lautet
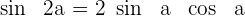
Beispiel 1: Berechne den Sinus von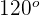 
1 Der Winkel 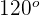kann wie folgt geschrieben werden
2 Wir berechnen den Sinus und den Kosinus für den gängigen Winkel 
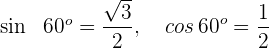
3 Wir setzen in die Formel für den Sinus eines Doppelwinkels ein
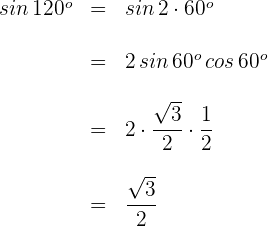
Beispiel 2: Berechne den Sinus von 
, wenn 
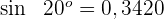und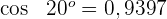 
1 Der Winkel kann wie folgt geschrieben werden
2 Die Werte des Sinus und Kosinus für den Winkel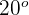 
sind hier angegeben, da es sich nicht um einen gängigen Winkel handelt
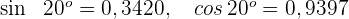
3 Wir setzen in die Formel für den Sinus eines Doppelwinkels ein
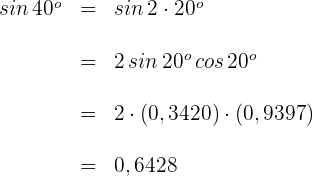
Es ist zu beachten, dass bei den gängigen Winkeln ein genaues Ergebnis erzielt wird, während bei den nicht gängigen Winkeln nur Näherungswerte erhalten werden.
Kosinus des Doppelwinkels
Die Formel zur Berechnung des Kosinus eines Doppelwinkels lautet
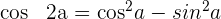
Beispiel 1: Berechne den Kosinus von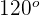
1 Der Winkel 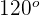kann wie folgt geschrieben werden
2 Wir berechnen die Werte des Sinus und des Kosinus für
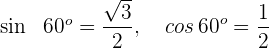
3 Wir setzen in die Formel für den Kosinus eines Doppelwinkels ein
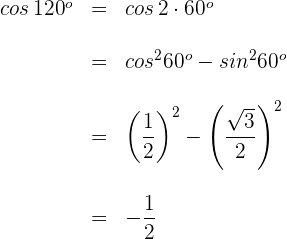
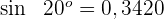Beispiel 2: Berechne den Kosinus von , wenn und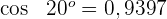
1 Der Winkel kann wie folgt geschrieben werden
2 Die Werte des Sinus und Kosinus für den Winkel 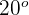sind hier angegeben, da es sich nicht um einen gängigen Winkel handelt
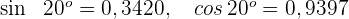
3 Wir setzen in die Formel für den Kosinus eines Doppelwinkels ein
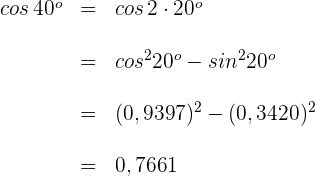
Beispiel 3: Berechne den Kosinus von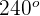 
1 Der Winkel 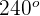kann wie folgt geschrieben werden
2 Die Werte des Sinus und Kosinus für 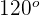sind
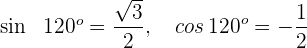
3 Wir setzen in die Formel für den Kosinus eines Doppelwinkels ein
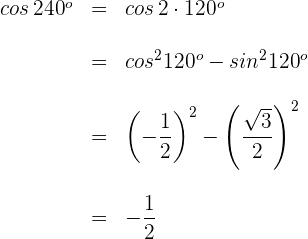
Tangens des Doppelwinkels
Die Formel zur Berechnung des Tangens eines Doppelwinkels lautet
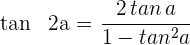
Beispiel 1: Berechne den Tangens von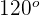
1 Der Winkel 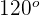kann wie folgt geschrieben werden
2 Wir ermitteln die Werte für den Tangens von
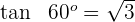
3 Wir setzen in die Formel für den Tangens eines Doppelwinkels ein
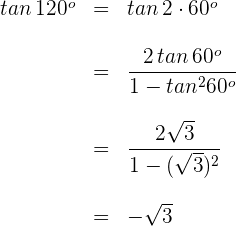
Beispiel 2: Berechne den Tangens von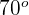 
, wenn 
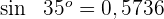und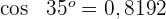 
1 Der Winkel 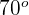kann als 
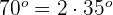geschrieben werden.
2 Wir ermitteln die Werte für den Tangens von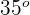 
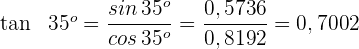
3 Wir setzen in die Formel für den Tangens eines Doppelwinkels ein
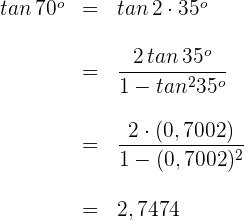
Beispiel 3: Berechne den Tangens von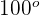 
, wenn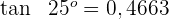 
1 Der Winkel 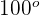wird als 
geschrieben und der Winkel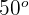 
als 
2 Der Wert für den Tangens von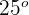 
ist gemäß den Daten durch 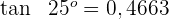gegeben.
3 Wir setzen in die Formel für den Tangens eines Doppelwinkels ein
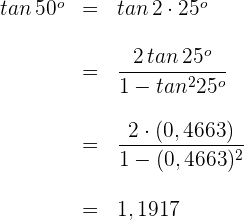
4 Wir setzen erneut in die Formel für den Tangens eines Doppelwinkels ein und erhalten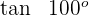 
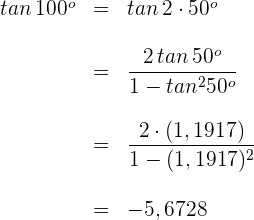
Denk daran, dass du bei den gängigen Winkeln ein exakte Ergebnis erhältst, während du bei nicht gängigen Winkeln nur Näherungswerte erhältst.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
