Kapitel
Ein Dreieck ist stumpfwinklig, wenn keines seiner Winkel rechtwinklig ist.
Zur Lösung stumpfwinkliger Dreiecke wenden wir den Sinus- und Kosinussatz an.
Je nach den uns bekannten Elementen gibt es vier Arten der Auflösung von stumpfwinkligen Dreiecken:
Eine Seite und zwei angrenzende Winkel sind bekannt
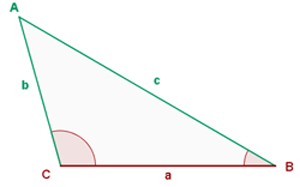
Wir nehmen an, dass die Seite 
und die angrenzenden Winkel 
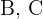bekannt sind. Um den Winkel und die übrigen Seiten zu finden, unternehmen wir folgende Schritte
1 Um den Winkel 
zu bestimmen, gehen wir wie folgt vor
2 Um 
zu berechnen, wenden wir den Sinussatz
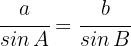
Wir multiplizieren beide Seiten der Gleichung mit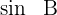 
und erhalten
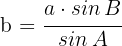
3 Um 
zu berechnen, wenden wir den Sinussatz an
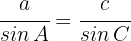
Wir multiplizieren beide Seiten der Gleichung mit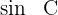 
und erhalten
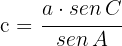
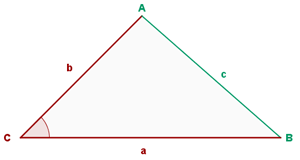
Zwei Seiten sowie der Winkel zwischen ihnen sind bekannt
Angenommen, die Seiten que se conocen los lados 
sowie der Winkel 
sind bekannt. Wir möchten nun die verbleibende Seite und die verbleibenden Winkel berechnen
1 Um die Seite zu berechnen, wenden wir den Kosinussatz an
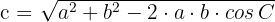
2 Für die Berechnung des Winkels 
wenden wir den Sinussatz an
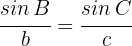
Wir multiplizieren beide Seiten der Gleichung mit und erhalten
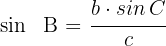
Wir ermitteln die Werte von 
, die die Gleichheit erfüllen. Beachte, dass es zwei Werte für gibt, einen im 1. Quadranten und einen im 2.
3 Um den fehlenden Winkel zu bestimmen, wenden wir das Ergebnis an, dass die Summe der Innenwinkel eines Dreiecks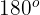 
ist, und bestimmen den Winkel, der uns interessiert. Dies müssen Sie für jeden der Werte von tun
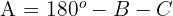
Um herauszufinden, welches der Winkelpaare richtig ist, musst du prüfen, welches der Paare den Sinussatz erfüllt.
Zwei Seiten und ein gegenüber liegender Winkel sind bekannt
Angenommen, die Seiten und der Winkel sind bekannt. Um die verbleibenden Seiten und Winkel zu berechnen, analysieren wir zunächst den Sinus des Winkels, der der bekannten Seite gegenüberliegt, mithilfe des Sinussatzes
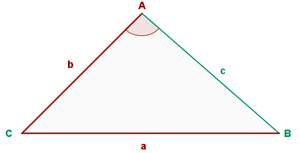
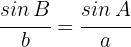
Wir ermitteln 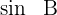und analysieren seinen Wert, um festzustellen, ob es eine Lösung gibt und ob es möglich ist, die restlichen Elemente des Dreiecks zu bestimmen.
Keine Lösung
Wenn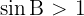 
, hat die Gleichung keine Lösung, da der Sinus eines Winkels nicht größer als 1 sein kann.
Eine einzige Lösung
Wenn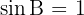 
, hat die Gleichung eine einzige Lösung 
, da es sich um ein rechtwinkliges Dreieck handelt.
Eine oder zwei Lösungen
Wenn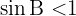 
, hat die Gleichung eine oder zwei Lösungen, abhängig von den Werten von :
Wenn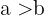 
gibt es eine Lösung.
Wenn 
gibt es zwei Lösungen.
Drei Seiten sind bekannt
Angenommen, alle drei Seiten des Dreiecks sind bekannt. Für die Winkel gehen wir wie folgt vor
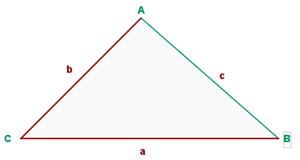
1 Um den ersten Winkel, sagen wir Winkel , zu finden, wenden wir den Kosinussatz an
Wir bestimmen 
und ermitteln , der sich im 1. Quadranten befindet
2 Um den zweiten Winkel zu berechnen, wenden wir wieder den Kosinussatz an
3 Wir berechnen den dritten Winkel
Aufgaben
Berechne die verbleibenden Elemente jedes der Dreiecke mit den folgenden Daten:
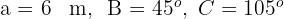
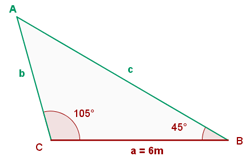
Da es sich um ein Dreieck handelt, von dem wir eine Seite und zwei angrenzende Winkel kennen, wenden wir die Formeln an, die wir zuvor für die erste Art der Auflösung erhalten haben.
1 Wir ermitteln den dritten Winkel 
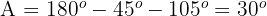
2 Um die Seite zu ermitteln, wenden wir den Sinussatz an und erhalten
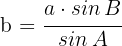
Wir setzen die bekannten Werte ein und erhalten
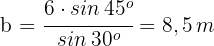
3 Um die fehlende Seite zu berechnen, wenden wir den Sinussatz an und erhalten
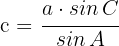
Wir setzen die bekannten Werte ein und erhalten
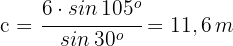
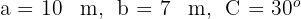
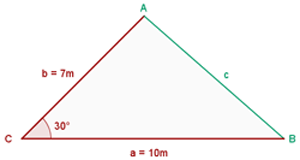
Da es sich um ein Dreieck handelt, bei dem wir zwei Seiten und die dazugehörigen Winkel kennen, wenden wir die Formeln an, die wir zuvor für die zweite Art der Auflösung erhalten haben.
1 Wir wenden den Kosinussatz an, um die dritte Seite 
zu berechnen
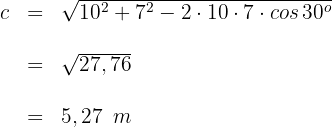
2 Wir wenden den Sinussatz an, um einen der beiden fehlenden Winkel zu berechnen
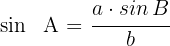
Wir setzen die bekannten Werte ein und erhalten
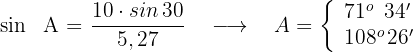
3 Wir berechnen nun den fehlenden Winkel. Beachte, dass für jeden der Werte von ein Wert ermittelt wird
Wenn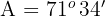 
, ist 
Wenn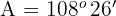 
, ist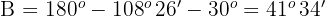 
Wir bestimmen, welches der Winkelpaare richtig ist
Wenn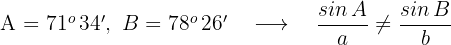 
Wenn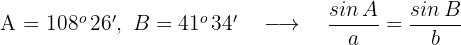 
Das gesuchte Winkelpaar ist also 
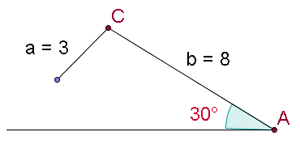
Da es sich um ein Dreieck handelt, bei dem wir zwei Seiten und einen gegenüberliegenden Winkel kennen, wenden wir die oben genannten Formeln für die dritte Art der Auflösung an
Mit dem Sinussatz erhalten wir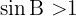 
. Da der Sinus eines Winkels niemals größer als 1 sein kann, gibt es keine Lösung für das Problem. Die Abbildung zeigt, dass es das betreffende Dreieck so nicht gibt.
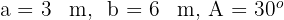
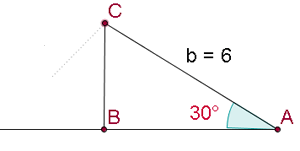
Da es sich um ein Dreieck handelt, bei dem wir zwei Seiten und einen gegenüberliegenden Winkel kennen, wenden wir die oben genannten Formeln für die dritte Art der Auflösung an.
1 Der Sinussatz zeigt uns, dass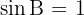 
und die Gleichung somit eine einzige Lösung, nämlich , hat. Es handelt sich also um ein rechtwinkliges Dreieck.
2 Wir berechnen den fehlenden Winkel
3 Mit dem Satz des Pythagoras berechnen wir die fehlende Seite
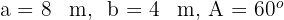
Da es sich um ein Dreieck handelt, bei dem wir zwei Seiten und einen entgegengesetzten Winkel kennen, wenden wir die Formeln an, die wir oben für die dritte Art der Auflösung erhalten haben.
1 Aus dem Sinussatz ergibt sich, dass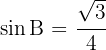 
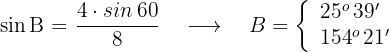
Da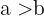 
, ist nur die Lösung 
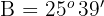gültig
3 Wir berechnen den fehlenden Winkel
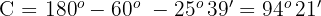
4 Wir wenden den Sinussatz an und berechnen die fehlende Seite
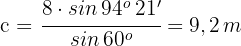
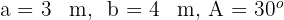
Da es sich um ein Dreieck handelt, bei dem wir zwei Seiten und einen gegenüberliegenden Winkel kennen, wenden wir die oben genannten Formeln für die dritte Art der Auflösung an
1 Aus dem Sinussatz ergibt sich, dass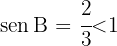 
. Die Gleichung hat somit eine oder zwei Lösungen
2 Wir berechnen die Werte für den Winkel
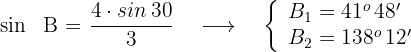
Da 
, sind beide Lösungen gültig
3 Wir berechnen den fehlenden Winkel
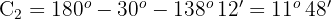
4 Wir wenden den Sinussatz an und berechnen die fehlende Seite
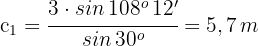
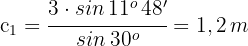
1 Um den ersten Winkel, also den Winkel , zu finden, wenden wir den Kosinussatz an, ermitteln und berechnen den Wert von , der im ersten Quadranten liegt
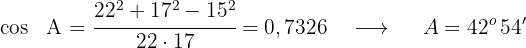
2 Um den zweiten Winkel zu berechnen, wenden wir wieder den Kosinussatz an und ermitteln den Wert im ersten Quadranten
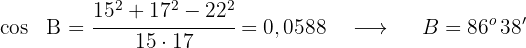
3 Wir berechnen den dritten Winkel
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
