Kapitel
- Winkelfunktionen
- Trigonometrischer Pythagoras
- Identitäten der Summe und Differenz von Winkeln
- Identitäten des Doppelwinkels und des Halbwinkels
- Identitäten mit Potenzen
- Umrechnung Summe – Produkt und umgekehrt
- Sinussatz, Kosinussatz und Tangenssatz
- Formel für die Berechnung der Fläche eines Dreiecks

Winkelfunktionen
Sehen wir uns das folgende rechtwinklige Dreieck an:
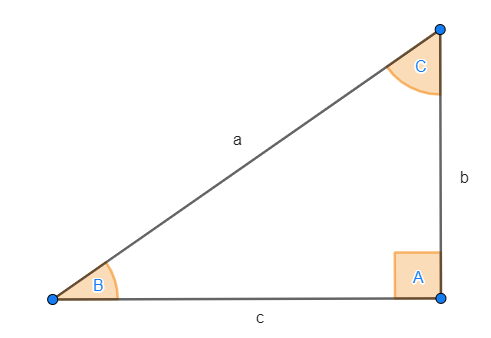
Die trigonometrischen Funktionen oder Winkelfunktionen definieren wir für den Winkel  wie folgt:
wie folgt:
1 Sinus:
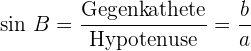
Manchmal wird der Sinus auch als 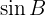 bezeichnet.
bezeichnet.
2 Kosinus:
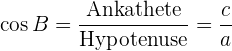
3 Tangens:
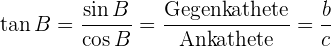
Der Tangens wird manchmal auch als 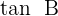 bezeichnet.
bezeichnet.
4 Kotangens:
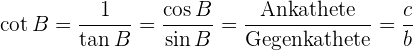
Der Kotangens wird manchmal auch als 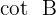 bezeichnet.
bezeichnet.
5 Sekans:
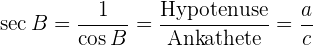
6 Kosekans:
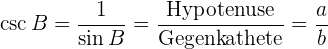
Der Kosekans wird manchmal auch als 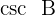 bezeichnet.
bezeichnet.
Bei den folgenden Identitäten verwenden wir  y
y  , um die Winkel (anstelle von
, um die Winkel (anstelle von  ,
,  oder
oder  ) zu benennen.
) zu benennen.
Trigonometrischer Pythagoras
Eine trigonometrische Identität ist eine Beziehung zwischen trigonometrischen Funktionen, die für alle Winkel  des Definitionsbereichs gilt. Diese Identitäten sind beim Lösen von Integralen, Differentialgleichungen und anderen mathematischen Problemen sehr nützlich.
des Definitionsbereichs gilt. Diese Identitäten sind beim Lösen von Integralen, Differentialgleichungen und anderen mathematischen Problemen sehr nützlich.
Da trigonometrische Funktionen durch rechtwinklige Dreiecke definiert sind, sind die folgenden Identitäten erfüllt:
1 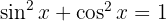
2 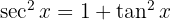
3 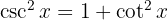
Identitäten der Summe und Differenz von Winkeln
1 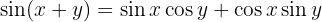
2 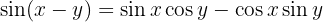
3 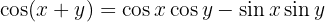
4 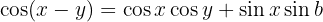
5 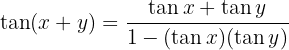
6 
Identitäten des Doppelwinkels und des Halbwinkels
Die Identitäten des Doppelwinkels erhalten wir über die Identitäten der Winkelsumme (mit  ). Die Identitäten des Halbwinkels erhalten wir hingegen über die Identität des Doppelwinkels von
). Die Identitäten des Halbwinkels erhalten wir hingegen über die Identität des Doppelwinkels von  .
.
Doppelwinkel
1 
2 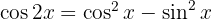
3 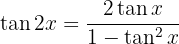
Halbwinkel
1 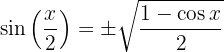
2 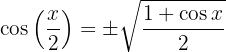
3 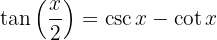
Beachte, dass der Tangens des Halbwinkels auch die folgenden Identitäten erfüllt:

und
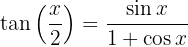
Identitäten mit Potenzen
1 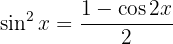
2 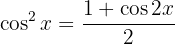
Umrechnung Summe – Produkt und umgekehrt
Umrechnung Summe – Produkt
1 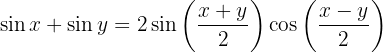
2 
3 
4 
5 
Umrechnung Produkt – Summe
1 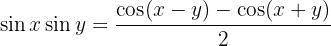
2 
3 
4 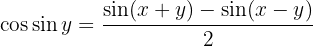
Sinussatz, Kosinussatz und Tangenssatz
Mit den Sätzen des Sinus, Kosinus und Tangens können wir Seiten oder Winkel berechnen, wenn unser Dreieck nicht rechwinklig ist. Sieh dir folgende Abbildung an:
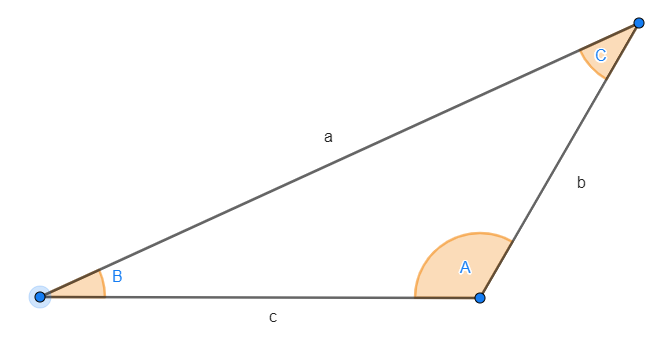
1 Sinussatz: Gegeben ist ein Dreieck (nicht unbedingt rechteckig) mit den Seiten  ,
,  und
und  mit den jeweiligen Winkeln
mit den jeweiligen Winkeln  ,
,  und
und  . Es gilt:
. Es gilt:

Hinweis: Wenn wir zwei Winkel und eine Seite haben, können mir mit dem Sinussatz die restlichen Seiten berechnen (den verbleibenden Winkel berechnen wir, indem wir uns daran erinnern, dass die Summe der Winkel gleich  ist).
ist).
2 Kosinussatz: Gegeben ist ein Dreieck (nicht unbedingt rechtwinklig) mit den Seiten  ,
,  und
und  mit den jeweiligen Winkeln
mit den jeweiligen Winkeln  ,
,  und
und  . Es gilt:
. Es gilt:
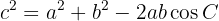
Außerdem ist Folgendes erfüllt:
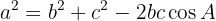
und
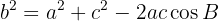
Hinweis: Wenn wir die Länge der drei Seiten haben, können wir mit dem Kosinussatz die Winkel berechnen. Ähnlich verhält es sich, wenn wir zwei Seiten und den Winkel zwischen ihnen haben. Dann verwenden wir den Kosinussatz, um die verbleibenden zwei Winkel und die verbleibende Seite zu berechnen.
3 Tangenssatz: Gegeben ist ein Dreieck (nicht unbedingt rechtwinklig) mit den Seiten  ,
,  und
und  mit den jeweiligen Winkeln
mit den jeweiligen Winkeln  ,
,  und
und  . Es gilt:
. Es gilt:

Formel für die Berechnung der Fläche eines Dreiecks
Schließlich sehen wir uns noch einige Formeln zur Berechnung des Flächeninhalts eines Dreiecks an. In diesen Formeln wird die Fläche mit  bezeichnet:
bezeichnet:
1 Wenn  die Basis und
die Basis und  die Höhe ist (die senkrecht zur Basis
die Höhe ist (die senkrecht zur Basis  steht), wird die Fläche wie folgt berechnet:
steht), wird die Fläche wie folgt berechnet:
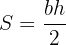
2 Gegeben ist das Dreieck mit den Seiten  ,
,  und
und  mit den jeweiligen Winkeln
mit den jeweiligen Winkeln  ,
,  und
und  . Die Fläche wird wie folgt berechnet:
. Die Fläche wird wie folgt berechnet:

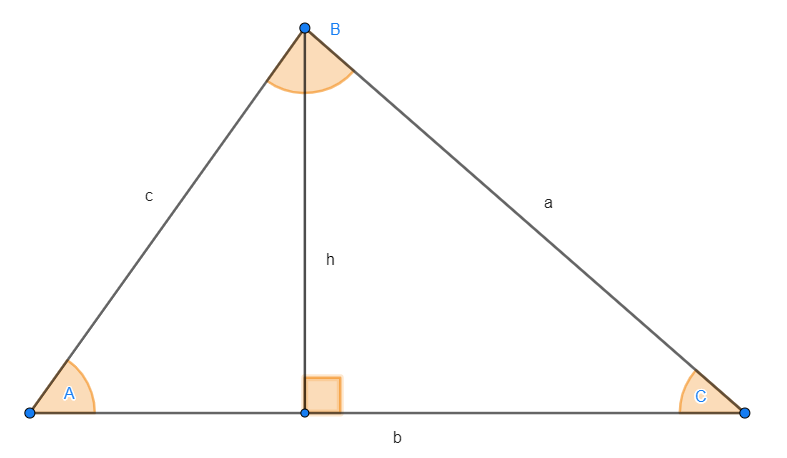
In der folgenden Abbildung sehen wir die Höhe, die senkrecht auf  steht. Daraus können wir schließen, dass
steht. Daraus können wir schließen, dass 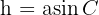 , woraus die Formel abgeleitet wird.
, woraus die Formel abgeleitet wird.
3 Wenn  den Radius dem Umkreises angibt, wird die Fläche wie folgt berechnet:
den Radius dem Umkreises angibt, wird die Fläche wie folgt berechnet:

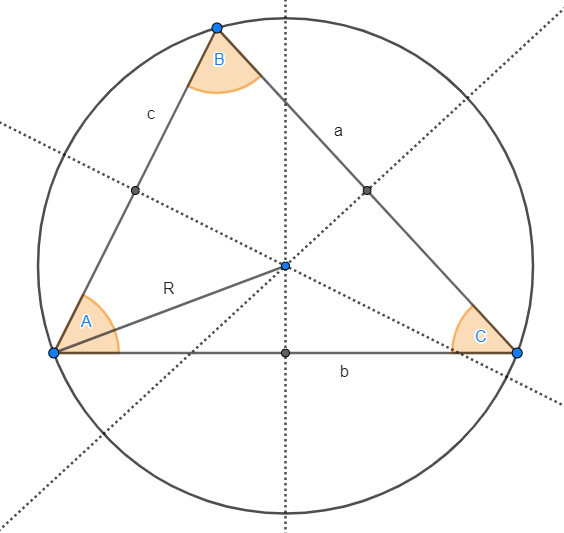
In der folgenden Abbildung sehen wir den Umkreis mit dem Radius  .
.
4 Wenn  den Radius eines Inkreies angibt, wird die Fläche wie folgt berechnet:
den Radius eines Inkreies angibt, wird die Fläche wie folgt berechnet:
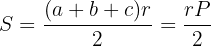 ,
,
wobei  der Umfang des Dreiecks ist.
der Umfang des Dreiecks ist.
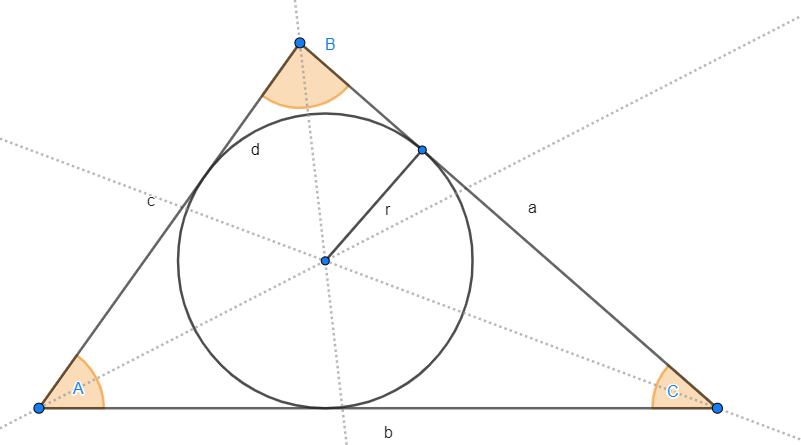
Folgende Abbildung zeigt den Inkreis.  ist dabei der Radius.
ist dabei der Radius.
5 Satz des Heron: 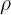 ist der halbe Umfang des Dreiecks mit den Seiten
ist der halbe Umfang des Dreiecks mit den Seiten  ,
,  und
und  . Das heißt
. Das heißt
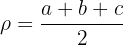
Die Fläche wird wie folgt berechnet
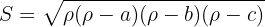
Mit KI zusammenfassen:












