Berechne für das folgende gleichschenklige Dreieck die Länge der unbekannten Seiten und die Winkel in jedem Fall: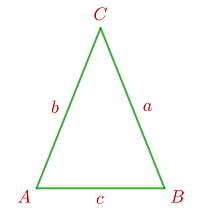 
Gegeben sind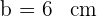 
und 
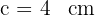. Berechne 
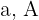und 
.
Bitte wähle eine Antwort aus.
Wir wissen, dass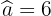 
, da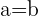 
gleichschenklig ist
Wir zeichnen die Seitenhalbierende, die durch 
verläuft und es entstehen zwei rechtwinklige Dreiecke der Seitenlänge 2 und der Hyptenuse 6. Wir ermitteln 
, indem wir die trigonometrischen Eigenschaften anwenden:
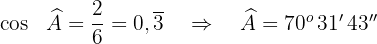
Da das Dreieck gleichschenklig ist, nämlich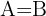 
, gilt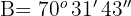 
Gegeben sind 
und 
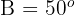. Berechne 
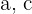und 
.
Bitte wähle eine Antwort aus.
Wir wissen, dass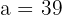 
, da 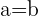gleichschenklig ist und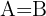 
Da die Summe der Seiten des Dreiecks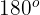 
ist, gilt:
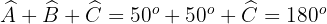
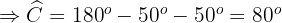
Um 
zu berechnen, wenden wir den Kosinussatz an
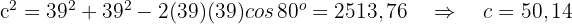
Gegeben sind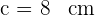 
und 
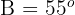. Berechne 
und .
Bitte wähle eine Antwort aus.
Wir wissen dass,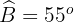 
. Da das Dreieck gleichschenklig ist, gilt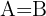
Da die Summe der Seiten des Dreiecks 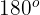ist, gilt:
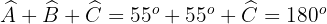
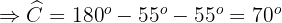
Wir zeichnen die Seitenhalbierende, die durch verläuft. Diese teilt das gleichschenklige Dreieck in zwei gleiche rechtwinklige Dreiecke. Wir berechnen 
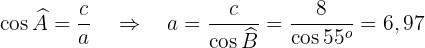
Wir wissen, dass 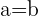, da das Dreieck gleichschenklig ist.
Gegeben sind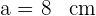 
und 
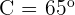. Berechne 
und .
Bitte wähle eine Antwort aus.
Wir wissen, dass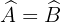 
und dass 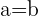, da das Dreieck gleichschenklig ist
Da die Summe der Seiten des Dreiecks 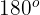ist, gilt:
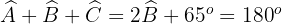
Wir wenden den Kosinussatz an:
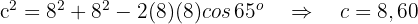
Berechne: (Runde, falls nötig, auf zwei Dezimalstellen)
Berechne die Höhe eines vertikalen Pfostens, wenn du weißt, dass an seinem oberen Ende zwei gleich lange Kabel gespannt sind, die sich im gleichen Abstand vom Pfostenfuß befinden. Wenn der Abstand zwischen den beiden Kabeln 
Meter beträgt und der Winkel zwischen ihnen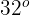 
misst, gilt
Höhe = 
Dieses Feld ist erforderlich.
Wir stellen fest, dass das Dreieck gleichschenklig ist, da die Länge der Kabel gleich ist.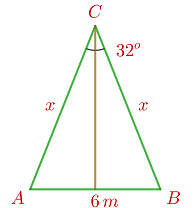 
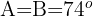. Wir berechnen die Höhe wie folgt:
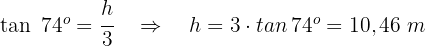
Eine Stadt liegt in gleicher Entfernung zu zwei Städten 
, die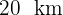 
voneinander entfernt sind. Der Winkel misst 
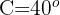. Wie weit liegt die Stadt von den Städten entfernt?
Abstand =
Dieses Feld ist erforderlich.
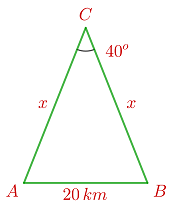
Wir stellen fest, dass es sich um ein gleichschenkliges Dreieck handelt. Wir wenden den Kosinussatz an
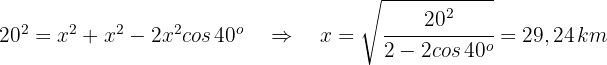
Zwei Personen befinden sich an einem Strand und sind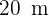 
voneinander entfernt. Beide beobachten ein Segelboot auf dem Meer, das ein gleichschenkliges Dreieck bildet, dessen Basiswinkel 
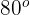betragen. Gib die Entfernung des Segelboots vom Strand an.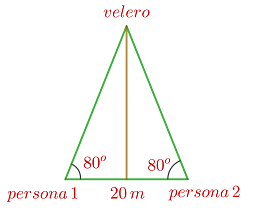 
Distanz =
Dieses Feld ist erforderlich.
Der Mast teilt also das gleichschenklige Dreieck in zwei gleiche rechtwinklige Dreiecke mit den Winkeln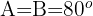 
. Um die Entfernung des Segelboots zum Strand zu berechnen, gehen wir wie folgt vor:
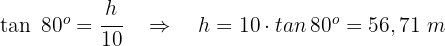
Um die Breite eines Flusses zu bestimmen, stellen sich zwei Personen auf derselben Seite des Flusses in einem Abstand von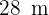 
voneinander auf und betrachten einen gemeinsamen Punkt am anderen Ufer, sodass ein Dreieck entsteht. Der Betrachtungswinkel der beiden Personen beträgt 
. Berechne die Breite des Flusses.
Breite =
Dieses Feld ist erforderlich.
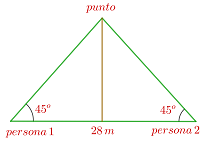
Die Breite teilt das gleichschenklige Dreieck in zwei gleiche rechtwinklige Dreiecke mit den Winkeln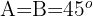 
. Um die Höhe zu berechnen, wenden wir calcular la altura aplicamos 
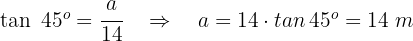an. Wir teilen das Dreieck in zwei rechtwinklige Dreiecke, um die trigonometrischen Eigenschaften anzuwenden. Wir lösen das System:
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
