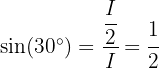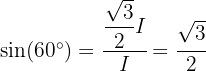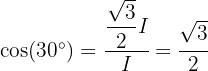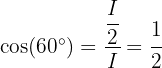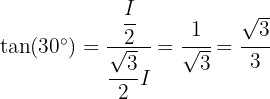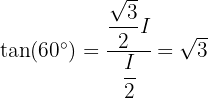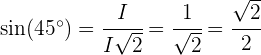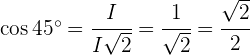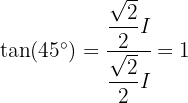Kapitel
In diesem Artikel werden wir die genauen Werte der Winkelfunktionen Sinus, Kosinus und Tangens für die Winkel 30°, 45° und 60° ermitteln. Diese Winkel bilden zusammen mit den Winkeln 0° und 90° einen Teil der bedeutendsten Winkel.

Sinus, Kosinus und Tangens von 30º und 60º
Um den Wert der Winkelfunktionen Sinus, Kosinus und Tangens von 30° und 60° zu ermitteln, zeichnen wir ein gleichseitiges Dreieck mit den Eckpunkten ABC, wie in der Abbildung gezeigt. Da es sich um ein gleichseitiges Dreieck handelt, misst jeder der drei Winkel 60°. Nun zeichnen wir die Höhe h ein, indem wir den Scheitelpunkt A halbieren. Das Ergebnis sind zwei Winkel von je 30°.
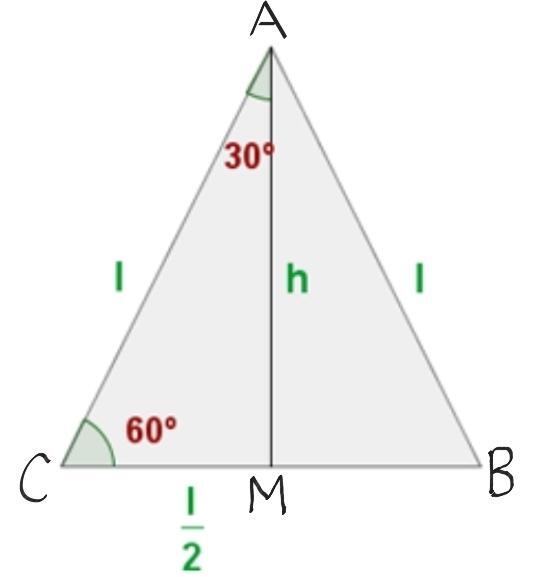
Wenn wir den Satz des Pythagoras auf das rechtwinklige Dreieck mit den Eckpunkten AMC anwenden, erhalten wir die Höhe:

Nun wenden wir die Definition der Winkelfunktionen in einem rechtwinkligen Dreieck and und erhalten
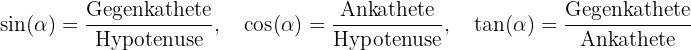
für einen Innenwinkel  des Dreiecks, mit Ausnahme des rechten Winkels. Somit ergibt sich
des Dreiecks, mit Ausnahme des rechten Winkels. Somit ergibt sich
Sinus, Kosinus und Tangens von 45º
Um den Wert der Winkelfunktionen Sinus, Kosinus und Tangens im Winkel von 45° zu erhalten, zeichnen wir ein Quadrat. Jeder Innenwinkel des Quadrats misst 90°. Wir zeichnen die Diagonale, die zwei der inneren Winkel halbiert, und erhalten einen Winkel von 45°.
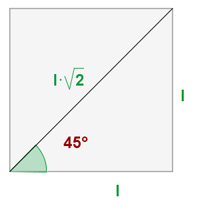
Wiederum unter Verwendung des Satzes des Pythagoras hat diese Diagonale eine Länge von

Aus der Definition der Winkelfunktionen in einem rechtwinkligen Dreieck ergibt sich wiederum, dass
Winkelfunktionen der gängigsten Winkel
Schließlich können wir alle Informationen, die wir in diesem Artikel aufgeführt haben, in der folgenden Tabelle zusammenfassen, der sogenannten Tabelle der Winkelfunktionen der gängigsten Winkel:
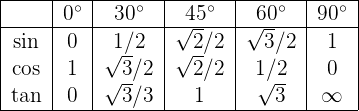
Um die Tabelle zu vervollständigen, haben wir hier die bekannten Werte der Winkelfunktionen für die Winkel 0° und 90° verwendet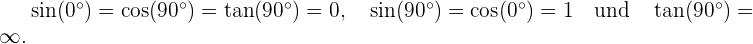
Mit KI zusammenfassen: