Kapitel
In diesem Fall müssen wir die fehlende Seite und die beiden fehlenden Winkel finden, wofür wir den Sinus- und Kosinussatz anwenden.
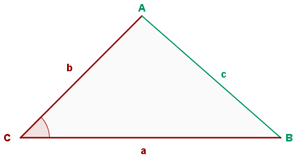
Angenommen, wir kennen die Seiten  und den Winkel
und den Winkel  zwischen ihnen. Um die restlichen Elemente zu finden, gehen wir wie folgt vor:
zwischen ihnen. Um die restlichen Elemente zu finden, gehen wir wie folgt vor:
1 Wir wenden den Kosinussatz an, um die dritte Seite  zu ermitteln
zu ermitteln
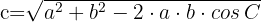
2 Wir wenden den Sinussatz an, um einen der beiden fehlenden Winkel zu bestimmen
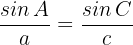
Wir ermitteln 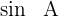 und suchen die Werte von
und suchen die Werte von  , die die Gleichheit erfüllen. Man beachte, dass es zwei Werte für
, die die Gleichheit erfüllen. Man beachte, dass es zwei Werte für  gibt, einen im ersten Quadranten und einen im zweiten Quadranten
gibt, einen im ersten Quadranten und einen im zweiten Quadranten
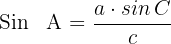
3 Um den fehlenden Winkel zu finden, wenden wir das Ergebnis an, dass die Summe der Innenwinkel eines Dreiecks 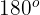 ist, und bestimmen den Winkel, der uns interessiert. Debes realizarlo para cada uno de los valores de
ist, und bestimmen den Winkel, der uns interessiert. Debes realizarlo para cada uno de los valores de 
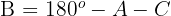
Um herauszufinden, welches der Winkelpaare richtig ist, müssen wir prüfen, welches der Paare den Sinussatz erfüllt

Beispiel 1
Folgende Werte sind bekannt:  und
und  . Berechne die verbleibenden Elemente.
. Berechne die verbleibenden Elemente.
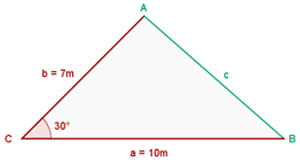
Um die gesuchten Elemente zu ermitteln, wenden wir den Sinus- und den Kosinussatz an, wie unten dargestellt
1 Wir wenden den Kosinussatz an, um die dritte Seite  zu bestimmen
zu bestimmen
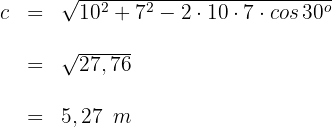
2 Wir wenden den Sinussatz an, um einen der beiden fehlenden Winkel zu ermitteln
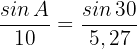
Wir ermitteln 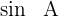 und somit den Wert von
und somit den Wert von 
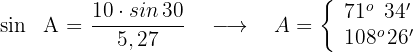
3 Wir ermitteln den fehlenden Winkel. Beachte, dass für wir für jeden der Werte von  einen Wert erhalten
einen Wert erhalten
Wenn 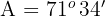 , ist
, ist 
Wenn 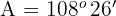 , ist
, ist 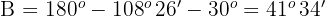
Wir bestimmen, welches der Winkelpaare richtig ist
Wenn 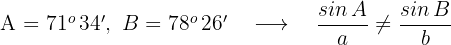
Wenn 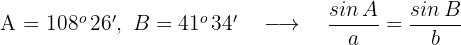
Somit ist das gesuchte Winkelpaar 
Beispiel 2
Folgende Werte sind bekannt:  und
und 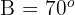 . Berechne die verbleibenden Elemente.
. Berechne die verbleibenden Elemente.
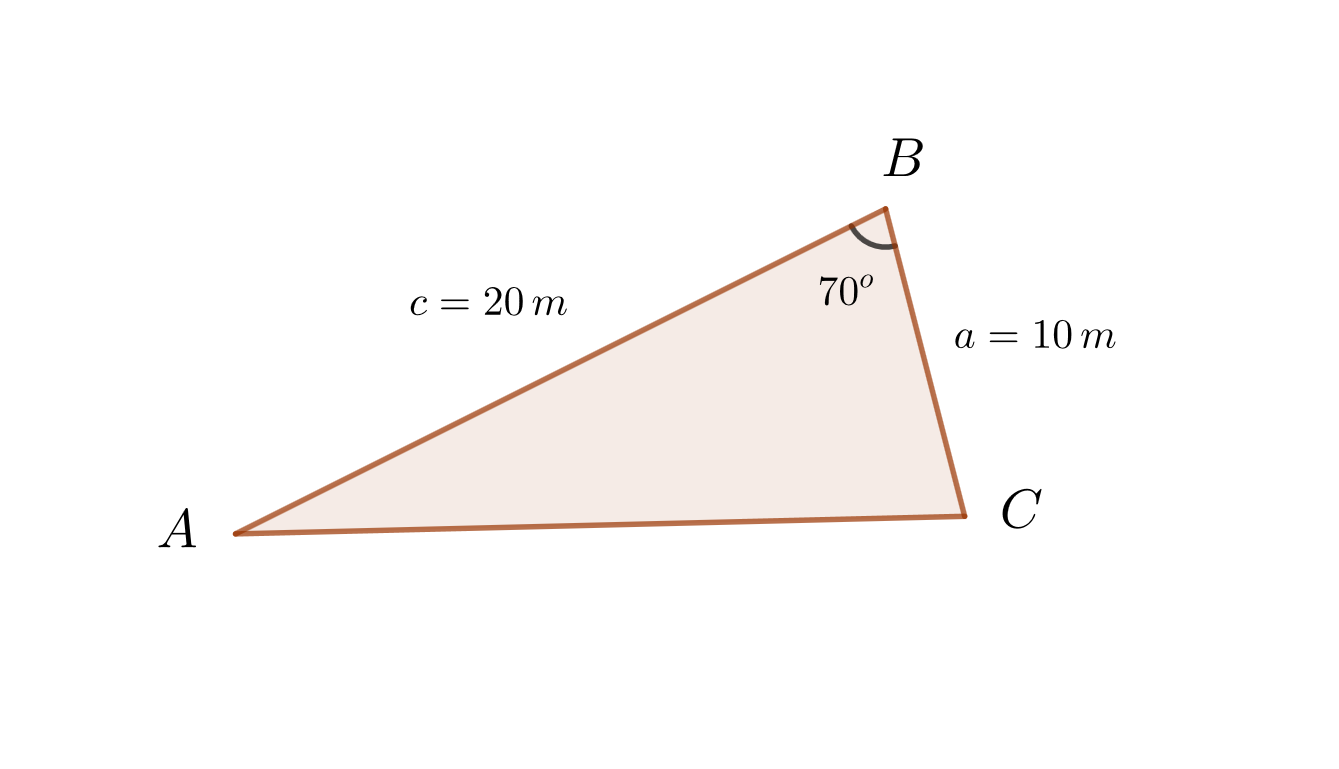
1 Wir wenden den Kosinussatz an, um die dritte Seite  zu ermitteln
zu ermitteln
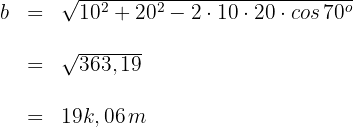
2 Wir wenden den Sinussatz an, um einen der beiden fehlenden Winkel zu ermitteln
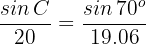
Wir ermitteln 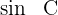 und erhalten den Wert von
und erhalten den Wert von 
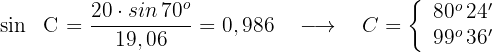
3 Wir ermitteln den fehlenden Winkel für jeden der Werte von 
Wenn 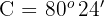 , ist
, ist 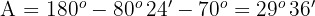
Wenn 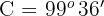 , ist
, ist 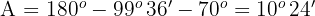
Wir berechnen, welches der Winkelpaare richtig ist
Wenn 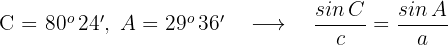
Wenn 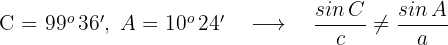
Somit ist  das gesuchte Winkelpaar
das gesuchte Winkelpaar
Beispiel 3
Folgende Werte sind bekannt: 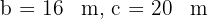 und
und 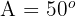 . Berechne die verbleibenden Elemente.
. Berechne die verbleibenden Elemente.
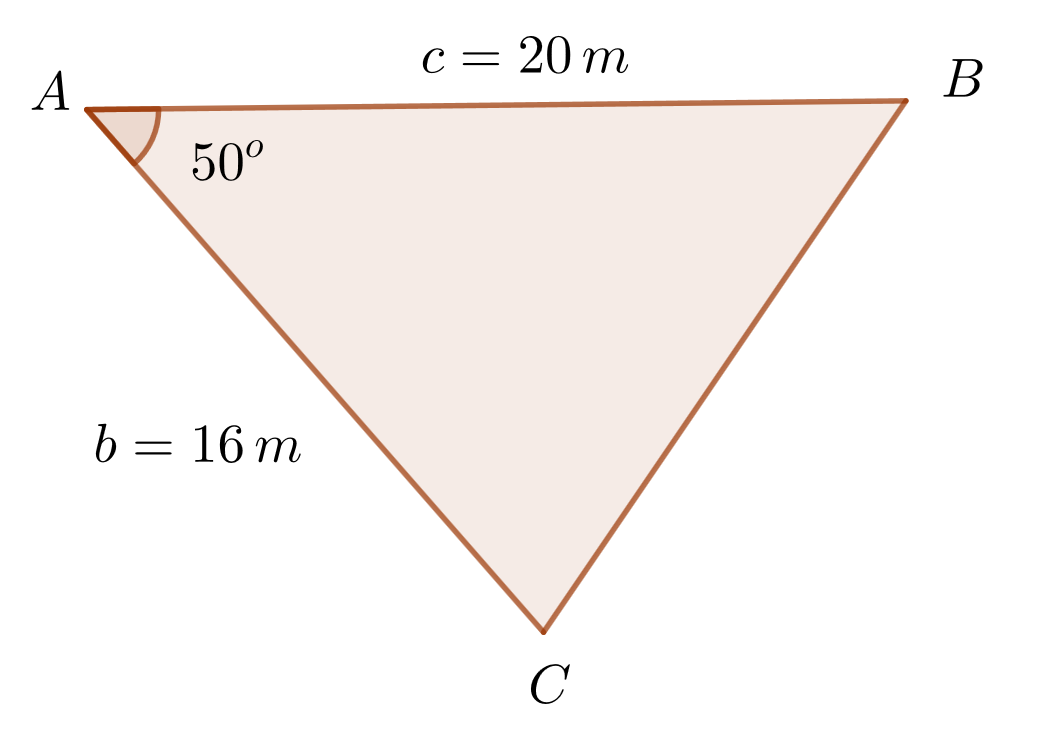
1 Wir wenden den Kosinussatz an, um die dritte Seite  zu finden
zu finden
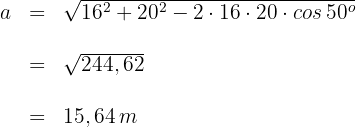
2 Wir wenden den Sinussatz an, um einen der beiden fehlenden Winkel zu ermitteln
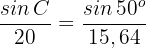
Wir ermitteln  und erhalten den Wert für
und erhalten den Wert für 
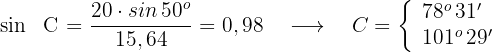
3 Wir ermitteln den fehlenden Winkel für jeden der Werte von 
Wenn 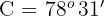 , ist
, ist 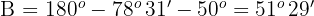
Wenn 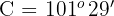 , ist
, ist 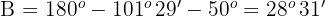
Wir bestimmen, welches der Winkelpaare richtig ist
Wenn 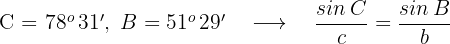
Wenn 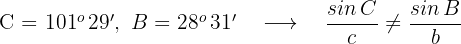
Somit ist  das gesuchte Winkelpaar.
das gesuchte Winkelpaar.
Mit KI zusammenfassen:












