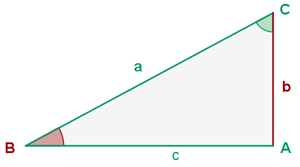
Gegeben ist ein rechtwinkliges Dreieck  mit
mit  und
und 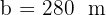 . Löse das Dreieck.
. Löse das Dreieck.
1
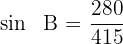
Wir wenden die Funktion 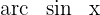 auf beiden Seiten der Gleichung an und erhalten
auf beiden Seiten der Gleichung an und erhalten
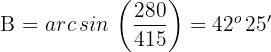
2
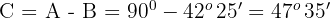
3
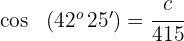
Wir bestimmen  und lösen
und lösen
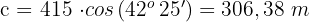
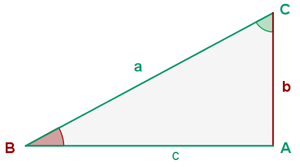
Gegeben ist ein rechtwinkliges Dreieck  mit
mit  und
und 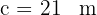 . Löse das Dreieck.
. Löse das Dreieck.
1
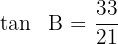
Wir wenden die Funktion 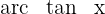 auf beiden Seiten der Gleichung an und erhalten
auf beiden Seiten der Gleichung an und erhalten
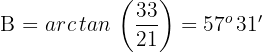
2
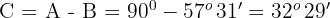
3
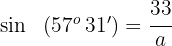
Wir bestimmen  und lösen
und lösen
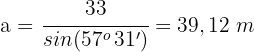
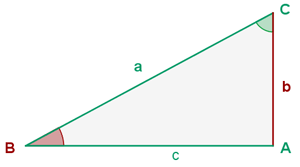
Gegeben ist ein rechtwinkliges Dreieck  mit
mit 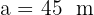 und
und  . Löse das Dreieck.
. Löse das Dreieck.
1
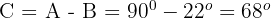
2
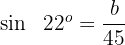
Wir bestimmen  und lösen
und lösen
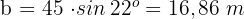
3
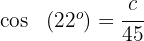
Wir bestimmen  und lösen
und lösen
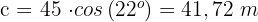
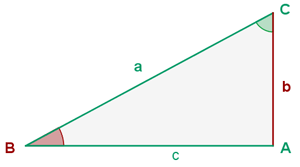
Gegeben ist ein rechtwinkliges Dreieck  mit
mit 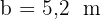 und
und 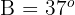 . Löse das Dreieck
. Löse das Dreieck
1 2 Wir bestimmen 3 Wir bestimmen 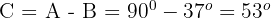
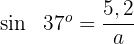
 und lösen
und lösen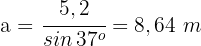
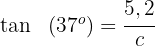
 und lösen
und lösen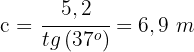
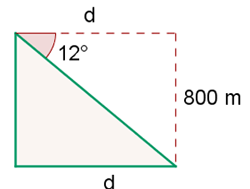
Ein Luftschiff fliegt in einer Höhe von  und bewegt sich in einem Winkel von
und bewegt sich in einem Winkel von  von einem Dorf weg. Wie weit entfernt vom Dorf befindet sich das Luftschiff?
von einem Dorf weg. Wie weit entfernt vom Dorf befindet sich das Luftschiff?
1
1
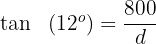
Wir bestimmen die Distanz  und lösen
und lösen
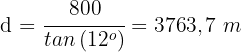
Ermittle den Radius eines Kreises, bei dem eine Sehne mit einer Länge von 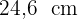 einen entsprechenden Bogen von
einen entsprechenden Bogen von 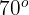 hat.
hat.
1 Wir stellen die uns bekannten Daten grafisch dar
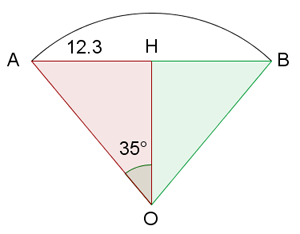
2Es ensteht ein gleichschenkliges Dreieck, dessen Seiten dem Radius des Kreises entsprechen. 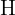 ist der Mittelpunkt des Segments
ist der Mittelpunkt des Segments  . Das Dreieck
. Das Dreieck 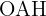 ist dann rechtwinklig und
ist dann rechtwinklig und 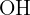 halbiert den Winkel
halbiert den Winkel 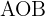
3Wir berechnen den Sinus des Winkels 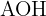
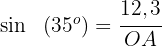
Wir ermitteln die Distanz  und lösen
und lösen
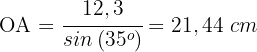
Der gesuchte Radius ist also 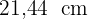 .
.
Berechne die Fläche eines dreieckigen Grundstücks, dessen Seiten 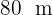 und
und 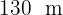 lang sind und einen Winkel von
lang sind und einen Winkel von 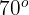 bilden.
bilden.
1 Wir stellen die uns bekannten Daten grafisch dar
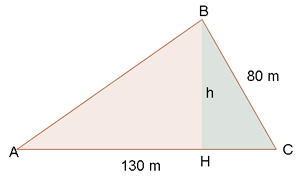
2Wir berechnen die Höhe  des Dreiecks. Hierzu berechnen wir den Sinus von
des Dreiecks. Hierzu berechnen wir den Sinus von 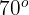
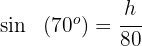
3Wir ermitteln  und lösen
und lösen
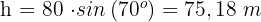
Die gesuchte Fläche ist
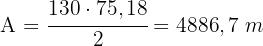
Berechne die Höhe eines Baums, wenn folgende Daten gegeben sind: Von einem Punkt am Boden aus sieht man, dass sich seine Krone um einen Winkel von 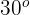 neigt und wenn wir uns
neigt und wenn wir uns  nähern, beträgt der Winkel
nähern, beträgt der Winkel 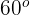 .
.
1 Wir stellen die uns bekannten Daten grafisch dar
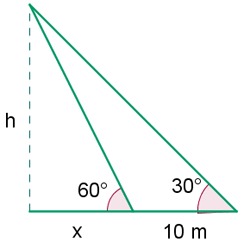
2Wir berechnen den Tangens von 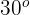 und bestimmen
und bestimmen 
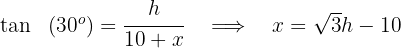
3Wir berechnen den Tangens von 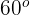 und bestimmen
und bestimmen 
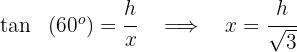
Wir setzen die beiden Werte für  gleich und lösen nach
gleich und lösen nach  auf
auf
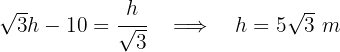
Die Länge der Seite eines regelmäßigen Achtecks beträgt  . Bestimme sowohl den Radius des Inkreises als auch den Radius des Umkreises.
. Bestimme sowohl den Radius des Inkreises als auch den Radius des Umkreises.
1 Wir stellen die uns bekannten Daten grafisch dar
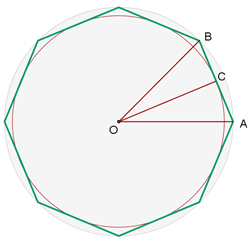
2 Der Winkel 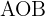 ist gleich
ist gleich 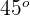 , weshalb der Winkel
, weshalb der Winkel  gleich
gleich  ist. Wir berechnen den Radius des Inkreises wie folgt
ist. Wir berechnen den Radius des Inkreises wie folgt
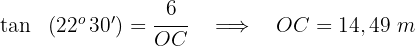
3 Wir berechnen den Radius des Umkreises wie folgt
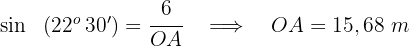
Berechne die Länge der Seite und des Apothemas eines regelmäßigen Achtecks, das einen Umkreis mit einem Radius von 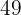 cm hat.
cm hat.
1Wir stellen die uns bekannten Daten grafisch dar
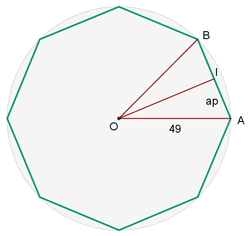
2 Der Winkel 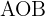 ist gleich
ist gleich 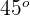 . Wenn wir also eine Winkelhalbierende einzeichnen, erhalten wir zwei gleiche, rechtwinklige Dreiecke. Wir berechnen die Seite wie folgt:
. Wenn wir also eine Winkelhalbierende einzeichnen, erhalten wir zwei gleiche, rechtwinklige Dreiecke. Wir berechnen die Seite wie folgt:
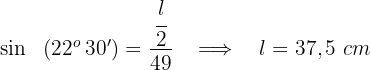
3 Wir berechnen das Apothema
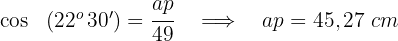
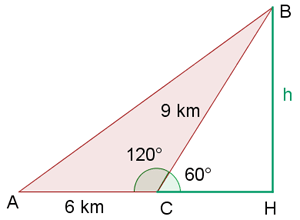
Drei Dörfer A, B und C sind durch Straßen verbunden. Die Entfernung von A nach C beträgt  km und von Dorf B nach C
km und von Dorf B nach C  km. Der Winkel, den diese Straßen bilden, beträgt
km. Der Winkel, den diese Straßen bilden, beträgt  . Wie weit liegen A und B voneinander entfernt?
. Wie weit liegen A und B voneinander entfernt?
1 Wir stellen die uns bekannten Daten grafisch dar und konstruieren ein rechtwinkliges Dreieck  , so dass
, so dass  auf dem Abschnitt
auf dem Abschnitt  liegt
liegt
2 Wir berechnen die Höhe
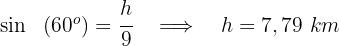
3 Wir berechnen die Distanz 
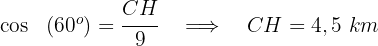
4 Wir berechnen die Distanz  mit dem Satz von Pythagoras
mit dem Satz von Pythagoras
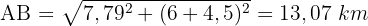
Mit KI zusammenfassen:



