Berechne die fehlende Seite des Dreiecks
Ein Dreieck  hat folgende Eigenschaften:
hat folgende Eigenschaften:
Die Hypotenuse:  .
.
Eine der Katheten: 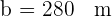
Löse das Dreieck.
Ein Dreieck  hat folgende Eigenschaften:
hat folgende Eigenschaften:
Die Hypotenuse:  .
.
Eine der Katheten: 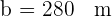
Löse das Dreieck.
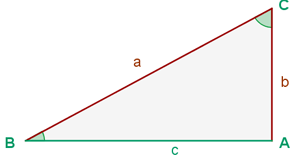
Das bedeutet, dass wir herausfinden müssen, wie lang die fehlende Seite ist und den Wert der Winkel berechnen müssen. Da das Dreieck rechtwinklig ist, ist der Winkel  .
.
Wir wenden den Sinus an und erhalten
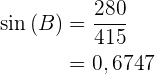
Mit dem Arkussinus erhalten wir den Winkel. Sobald wir zwei Winkel haben, können wir direkt den letzten Winkel berechnen;
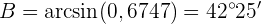
Nun haben wir zwei Winkel und berechnen den Letzten:

Beim Winkel  wenden wir den Kosinus an und ermitteln den Wert der Seite
wenden wir den Kosinus an und ermitteln den Wert der Seite  :
:
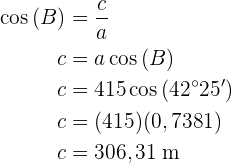
So einfach konnten wir die fehlenden Daten ermitteln.
a berechnen, wenn b und c bekannt sind
Gegeben ist ein Dreieck  mit den Katheten
mit den Katheten
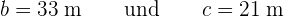
Löse das Dreieck.
Gegeben ist ein Dreieck  mit den Katheten
mit den Katheten
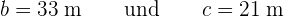
Löse das Dreieck.
Wir müssen also die fehlenden Seiten und Winkel berechnen. Da das Dreieck rechtwinklig ist, haben wir auch den Winkel  .
.
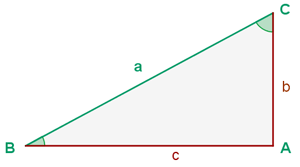
Um den Winkel  zu bestimmen, berechnen wir seinen Tangens und wenden dann den Arkustangens an:
zu bestimmen, berechnen wir seinen Tangens und wenden dann den Arkustangens an:
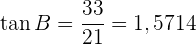
Wir wenden den Arkustangens an und erhalten 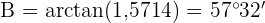 . So erhalten wir zwei Winkel und können den Dritten,
. So erhalten wir zwei Winkel und können den Dritten,  , direkt berechnen:
, direkt berechnen:
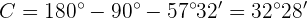
Als Letztes müssen wir noch die Seite  berechnen. Hierfür nutzen wir den Sinus und wenden ihn auf den Winkel
berechnen. Hierfür nutzen wir den Sinus und wenden ihn auf den Winkel  an. Danach berechnen wir
an. Danach berechnen wir  .
.
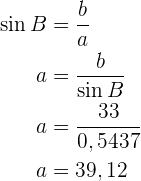
So einfach konnten wir die fehlenden Daten ermitteln.
Löse das Dreieck, wenn eine Seite und ein Winkel bekannt sind
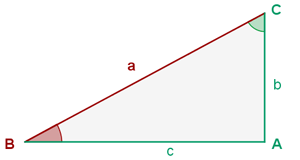
Gegeben ist ein Dreieck  mit der Hypotenuse und einem Winkel
mit der Hypotenuse und einem Winkel

Löse das Dreieck.
Gegeben ist ein Dreieck  mit der Hypotenuse und einem Winkel
mit der Hypotenuse und einem Winkel

Löse das Dreieck.
Wir müssen also die fehlenden Seiten und Winkel berechnen. Da das Dreieck rechtwinklig ist, haben wir auch den Winkel  .
.
Da zwei Winkel bekannt sind, können wir den Dritten,  , direkt berechnen:
, direkt berechnen:
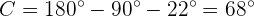
Um die Seite  zu erhalten, wenden wir den Sinus auf den Winkel
zu erhalten, wenden wir den Sinus auf den Winkel  an und ermitteln
an und ermitteln  :
:
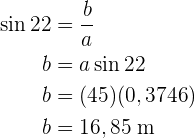
Um die Seite  zu erhalten, wenden wir den Kosinus auf den Winkel
zu erhalten, wenden wir den Kosinus auf den Winkel  an und ermitteln
an und ermitteln  :
:
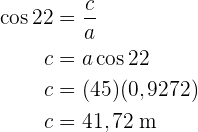
So haben wir die fehlenden Seiten und Winkel ermittelt.
Löse das Dreieck, bei dem eine Seite und ein Winkel gegeben ist
Gegeben ist ein Dreieck  mit einer Kathete und einem Winkel
mit einer Kathete und einem Winkel

Löse das Dreieck.
Gegeben ist ein Dreieck  mit einer Kathete und einem Winkel
mit einer Kathete und einem Winkel

Löse das Dreieck.
Wir berechnen die fehlenden Seiten und Winkel. Da es sich um ein rechtwinkliges Dreieck handelt, wissen wir bereits im Voraus, dass ein Winkel ist.
ist.
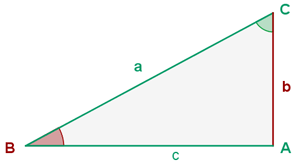
Da zwei von drei Winkeln bekannt sind, können wir den fehlenden Winkel  direkt berechnen.
direkt berechnen.
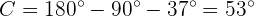
Um die Seite  zu erhalten, wenden wir den Sinus auf den Winkel
zu erhalten, wenden wir den Sinus auf den Winkel  an und bestimmen
an und bestimmen  :
:
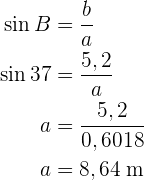
Um die Seite  zu erhalten, wenden wir den Kotangens auf den Winkel
zu erhalten, wenden wir den Kotangens auf den Winkel  an und bestimmen
an und bestimmen  :
:
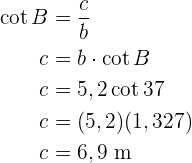
Wir haben die fehlenden Seiten und Winkel berechnet.
Löse folgendes rechtwinkliges Dreieck
Gegeben ist ein Dreieck  mit der Hypotenuse und einem Winkel
mit der Hypotenuse und einem Winkel

Löse das Dreieck.
Gegeben ist ein Dreieck  mit der Hypotenuse und einem Winkel
mit der Hypotenuse und einem Winkel

Löse das Dreieck.
Wir ermitteln die fehlenden Seiten. Da es sich um ein rechtwinkliges Dreieck handelt, wissen wir bereits im Voraus, dass ein Winkel ist.
ist.
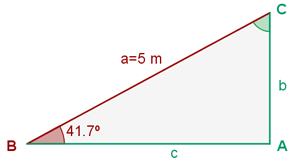
Da zwei von drei Winkeln bekannt sind, können wir den fehlenden Winkel  direkt berechnen.
direkt berechnen.
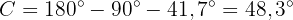
Um die Seite  zu erhalten, wenden wir den Sinus auf den Winkel
zu erhalten, wenden wir den Sinus auf den Winkel  an und bestimmen
an und bestimmen  :
:
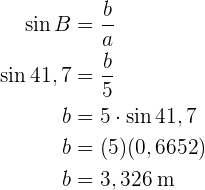
Um die Seite  zu ermitteln, wenden wir den Kosinus auf den Winkel
zu ermitteln, wenden wir den Kosinus auf den Winkel  an und bestimmen
an und bestimmen  :
:
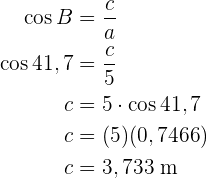
Wir haben die fehlenden Seiten und Winkel berechnet.
Berechne die fehlenden Daten des folgenden Dreiecks
Gegeben ist ein Dreieck  mit einer Kathete und einem Winkel
mit einer Kathete und einem Winkel

Löse das Dreieck.
Gegeben ist ein Dreieck  mit einer Kathete und einem Winkel
mit einer Kathete und einem Winkel

Löse das Dreieck.
Wir ermitteln die fehlenden Seiten und Winkel. Da es sich um ein rechtwinkliges Dreieck handelt, wissen wir bereits im Voraus, dass ein Winkel ist.
ist.
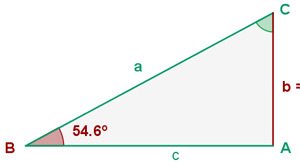
Da zwei von drei Winkeln bekannt sind, können wir den fehlenden Winkel  direkt berechnen
direkt berechnen
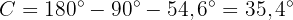
Um die Seite  zu berechnen, wenden wir den Tangens auf den Winkel
zu berechnen, wenden wir den Tangens auf den Winkel  an und bestimmen
an und bestimmen  :
:
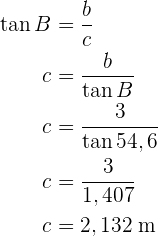
Um die Seite  zu ermitteln, wenden wir den Sinus auf den Winkel
zu ermitteln, wenden wir den Sinus auf den Winkel  an und bestimmen
an und bestimmen  :
:
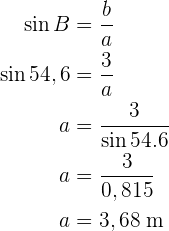
Wir haben die fehlenden Seiten und Winkel berechnet.
Zwei Seiten eines Dreiecks sind gegeben
Gegeben ist ein rechtwinkliges Dreieck  mit der Hypotenuse und einer Kathete
mit der Hypotenuse und einer Kathete

Löse das Dreieck.
Gegeben ist ein Dreieck  mit der Hyptenuse und einer Kathete
mit der Hyptenuse und einer Kathete

Löse das Dreieck.
Wir ermitteln die fehlenden Seiten und Winkel. Da es sich um ein rechtwinkliges Dreieck handelt, wissen wir bereits im Voraus, dass ein Winkel ist.
ist.
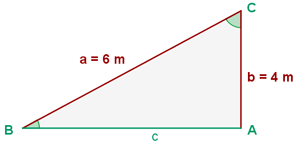
Um den Winkel  zu ermitteln, berechnen wir als Erstes des Kosinus des Winkels mithilfe der Kathete und der Hypotenuse. So können wir dann die Umkehrfunktion, den Arkuskosinus, anwenden.
zu ermitteln, berechnen wir als Erstes des Kosinus des Winkels mithilfe der Kathete und der Hypotenuse. So können wir dann die Umkehrfunktion, den Arkuskosinus, anwenden.
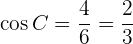
Wir wenden den Arkuskosinus an und erhalten 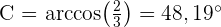 . Da wir zwei Winkel bereits haben, können wir den Dritten direkt berechnen
. Da wir zwei Winkel bereits haben, können wir den Dritten direkt berechnen
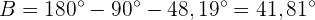
Um die Seite  zu ermitteln, wenden wir den Sinus auf den Winkel
zu ermitteln, wenden wir den Sinus auf den Winkel  und ermitteln
und ermitteln  :
:
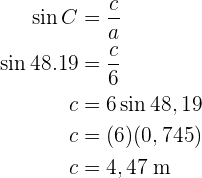
Wir haben die fehlenden Seiten und Winkel berechnet.
Löse folgendes Dreieck
Gegeben ist ein Dreieck  mit den zwei Katheten
mit den zwei Katheten

Löse das Dreieck.
Gegeben ist ein Dreieck  mit den zwei Katheten
mit den zwei Katheten

Löse das Dreieck.
Wir ermitteln die fehlenden Seiten und Winkel. Da es sich um ein rechtwinkliges Dreieck handelt, wissen wir bereits im Voraus, dass ein Winkel ist.
ist.
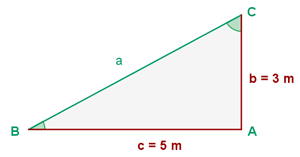
Um den Winkel  zu ermitteln, berechnen wir zunächst seinen Tangens und nutzen hierfür die Katheten. Im Anschluss können wir den Arkustangens berechnen
zu ermitteln, berechnen wir zunächst seinen Tangens und nutzen hierfür die Katheten. Im Anschluss können wir den Arkustangens berechnen
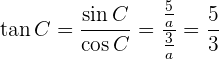
Wir erhalten also 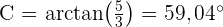 . Und da wir nun zwei Winkel haben, können wir den Dritten direkt berechnen
. Und da wir nun zwei Winkel haben, können wir den Dritten direkt berechnen
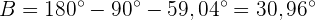
Um die Seite  zu ermitteln, wenden wir den Sinus auf den Winkel
zu ermitteln, wenden wir den Sinus auf den Winkel  an und bestimmen
an und bestimmen  :
:
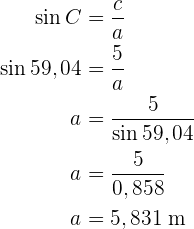
Wir haben die fehlenden Seiten und Winkel berechnet.
Ein Baum und sein Schatten
Ein Baum mit einer Höhe von  wirft einen Schatten, der
wirft einen Schatten, der  lang ist.
lang ist.
Berechne den Höhenwinkel der Sonne in diesem Moment.
Ein Baum mit einer Höhe von  wirft einen Schatten, der
wirft einen Schatten, der  lang ist.
lang ist.
Berechne den Höhenwinkel der Sonne in diesem Moment.
Zwischen dem Boden und dem Baum entsteht ein Winkel von  . Somit haben wir zwei Katheten. Außerdem ist der Höhenwinkel der Winkel, der am Scheitelpunkt entsteht, wo der Schatten aufhört.
. Somit haben wir zwei Katheten. Außerdem ist der Höhenwinkel der Winkel, der am Scheitelpunkt entsteht, wo der Schatten aufhört.
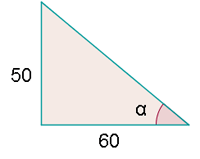
Um also den Höhenwinkel  ermitteln zu können, berechnen wir zunächst seinen Tangens mithilfe der Katheten und wenden danach den Arkustangens auf unser Ergebnis an
ermitteln zu können, berechnen wir zunächst seinen Tangens mithilfe der Katheten und wenden danach den Arkustangens auf unser Ergebnis an
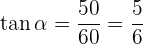
Wir erhalten somit  .
.
Berechne den Abstand anhand der vorherigen Dreiecke
Ein Luftschiff fliegt in einer Höhe von 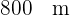 und bewegt sich in einem Winkel von
und bewegt sich in einem Winkel von 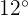 von einem Dorf weg.
von einem Dorf weg.
Wie weit ist das Luftschiff vom Dorf entfernt?
Ein Luftschiff fliegt in einer Höhe von 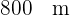 und bewegt sich in einem Winkel von
und bewegt sich in einem Winkel von 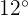 von einem Dorf weg.
von einem Dorf weg.
Wie weit ist das Luftschiff vom Dorf entfernt?
Mit den gegebenen Daten können wir den Sachverhalt grafisch darstellen.
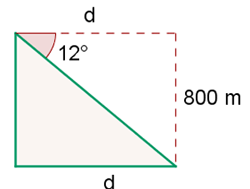
Wir möchten herausfinden, wie weit das Luftschiff vom Dorf entfernt ist. Wir müssen also die Kathete  berechnen. Hierzu berechnen wir den Tangens des Winkels mit dem Wert
berechnen. Hierzu berechnen wir den Tangens des Winkels mit dem Wert 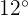 und nutzen zugleich die Katheten. Nun können wir
und nutzen zugleich die Katheten. Nun können wir  bestimmen:
bestimmen:
Berechne den Radius des Kreises
Berechne den Radius eines Kreises, wenn eine Sehne 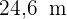 lang ist und der entsprechende Bogen
lang ist und der entsprechende Bogen  misst.
misst.
Der Mittelpunktswinkel misst genauso viel wie der Bogen, der ihn umspannt. Wir haben also
Um den Radius zu ermitteln (Seite ), wenden wir den Sinus auf den Winkel an, der
), wenden wir den Sinus auf den Winkel an, der  beträgt, indem wir die bekannte Kathete und
beträgt, indem wir die bekannte Kathete und  nutzen, um danach den Radius berechnen zu können:
nutzen, um danach den Radius berechnen zu können:
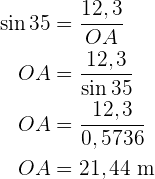
Berechne die Fläche, wenn ein Winkel und 2 Seiten bekannt sind
Berechne die Fläche eines dreieckigen Grundstücks, dessen Seiten 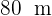 und
und 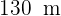 lang sind und einen Winkel von
lang sind und einen Winkel von  bilden.
bilden.
Berechne die Fläche eines dreieckigen Grundstücks, dessen Seiten 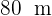 und
und 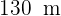 lang sind und einen Winkel von
lang sind und einen Winkel von  bilden.
bilden.
Wir haben also den Winkel 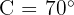 und können uns folgende Grafik ansehen, die das Dreieck darstellt.
und können uns folgende Grafik ansehen, die das Dreieck darstellt.
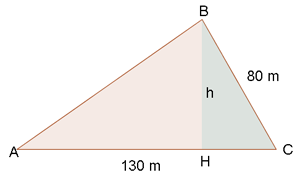
Wir sehen, dass die Höhe unser ursprüngliches Dreieck in zwei rechtwinklige Dreiecke teilt. Wir nehmen das rechte Dreieck, da wir mehr darüber wissen, um die Höhe und schließlich die Fläche zu berechnen. Für die Höhe nutzen wir den Sinus des Winkels  , die zu diesem Dreieck gehörende Kathete und die Höhe, die wir so schließlich berechnen können:
, die zu diesem Dreieck gehörende Kathete und die Höhe, die wir so schließlich berechnen können:
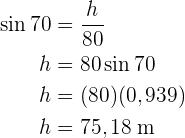
Die Höhe beträgt also 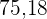 und wir können nun die Fläche berechnen:
und wir können nun die Fläche berechnen:
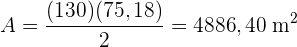
Berechne die Höhe des Baums
Berechne die Höhe des Baums mit folgenden Informationen: Von einem Punkt am Boden aus kann man sehen, dass sich die Krone um einen Winkel von  neigt und wenn wir uns
neigt und wenn wir uns  nähern, beträgt der Winkel
nähern, beträgt der Winkel  .
.
Zum besseren Verständnis versuchen wir, das Problem mit der folgenden Zeichnung darzustellen
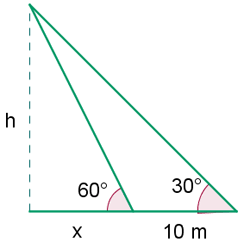
Um das Problem zu lösen, berechnen wir zunächst den Tangens des Winkels von  und den zugehörigen Katheten. Danach berechnen wir den Tangens des Winkels von
und den zugehörigen Katheten. Danach berechnen wir den Tangens des Winkels von 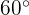 mit den zugehörigen Katheten und bestimmen
mit den zugehörigen Katheten und bestimmen  für beide:
für beide:
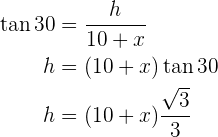
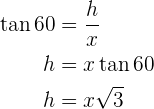
Wir erhalten ein Gleichungssystem
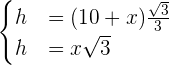
Wir lösen das System und erhalten 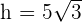 .
.
Radius berechnen
Die Länge der Seite eines regelmäßigen Achtecks beträgt  . Bestimme den Radius des Inkreises und den Radius des Umkreises.
. Bestimme den Radius des Inkreises und den Radius des Umkreises.
Die folgende Grafik zeigt uns das Achteck sowie den Inkreis und den Umkreis.
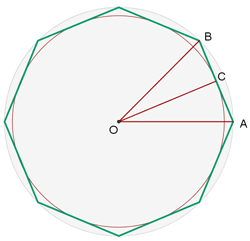
Gegeben ist die Seite  . Außerdem stellt die Seite
. Außerdem stellt die Seite 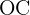 den Radius des Inkreises dar und die Seite
den Radius des Inkreises dar und die Seite 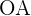 den Radius des Umkreises. Wir wissen auch, dass der Winkel
den Radius des Umkreises. Wir wissen auch, dass der Winkel  beträgt und da es sich um ein Achteck handelt, haben wir
beträgt und da es sich um ein Achteck handelt, haben wir  .
.
Radius des Inkreises
Wir berechnen den Tangens des Winkels 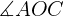 . Hierfür nehmen wir den Wert des Winkels sowie der Katheten und können so schließlich die Kathete
. Hierfür nehmen wir den Wert des Winkels sowie der Katheten und können so schließlich die Kathete 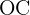 berechnen.
berechnen.
Radius des Umkreises
Wir berechnen den Sinus des Winkels 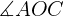 . Hierfür nutzen wir sowohl den Winkel also auch die Kathete und die Hyptenuse, um schließlich die Hypotenuse
. Hierfür nutzen wir sowohl den Winkel also auch die Kathete und die Hyptenuse, um schließlich die Hypotenuse 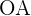 ermitteln zu können.
ermitteln zu können.
Berechne die Seite und das Apothema des Achtecks
Berechne die Länge der Seite und des Apothema eines regelmäßigen Achtecks, das in einem Kreis mit einem Radius von 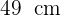 liegt.
liegt.
Mit der folgenden Grafik können wir uns das Problem besser vorstellen.
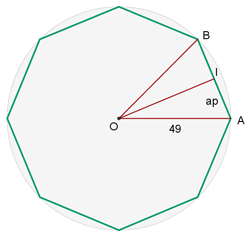
Der Radius entspricht der Seite 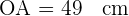 . Nun ist die Seite des Achtecks gegeben durch
. Nun ist die Seite des Achtecks gegeben durch  sowie
sowie 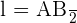 .
.
Außerdem sehen wir, dass das Apothema 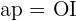 den Winkel
den Winkel  in zwei Teile teilt. Der Winkel beträgt
in zwei Teile teilt. Der Winkel beträgt  und da es sich um ein Achteck handelt, gilt
und da es sich um ein Achteck handelt, gilt 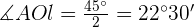 . Die Seiten
. Die Seiten 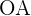 ,
,  und
und 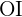 bilden zudem ein rechtwinkliges Dreieck.
bilden zudem ein rechtwinkliges Dreieck.
Seite des Achtecks
Wir berechnen den Sinus des Winkels 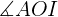 . Hierfür nutzen wir den Wert des Winkels und die Hypotenuse (Radius des Achtecks) sowie die Kathete (die Hälfte der Seite des Achtecks). So können wir schließlich die Kathete
. Hierfür nutzen wir den Wert des Winkels und die Hypotenuse (Radius des Achtecks) sowie die Kathete (die Hälfte der Seite des Achtecks). So können wir schließlich die Kathete  ermitteln.
ermitteln.
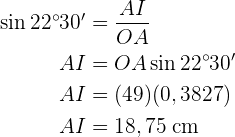
Die Seite ist also 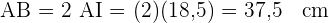 lang.
lang.
Apothema des Achtecks
Wir berechnen den Kosinus des Winkels 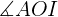 . Hierfür nutzen wir den Winkel und die Hypotenuse (den Radius des Achtecks) und die Kathete (das Apothema), um schließlich die Kathete
. Hierfür nutzen wir den Winkel und die Hypotenuse (den Radius des Achtecks) und die Kathete (das Apothema), um schließlich die Kathete 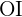 berechnen zu können.
berechnen zu können.
Entfernung zwischen zwei Dörfern
Drei Dörfer  ,
,  und
und  sind durch eine Straße miteinander verbunden. Die Entfernung von
sind durch eine Straße miteinander verbunden. Die Entfernung von  nach
nach  beträgt
beträgt 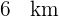 und von
und von  nach
nach  sind es
sind es 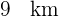 . Außerdem beträgt der Winkel, den die Straßen bilden,
. Außerdem beträgt der Winkel, den die Straßen bilden, 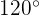 .
.
Wie weit liegen  und
und  auseinander?
auseinander?
Drei Dörfer  ,
,  und
und  sind durch eine Straße miteinander verbunden. Die Entfernung von
sind durch eine Straße miteinander verbunden. Die Entfernung von  nach
nach  beträgt
beträgt 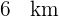 und von
und von  nach
nach  sind es
sind es 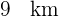 . Außerdem beträgt der Winkel, den die Straßen bilden,
. Außerdem beträgt der Winkel, den die Straßen bilden, 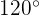 .
.
Wie weit liegen  und
und  auseinander?
auseinander?
Mit der folgenden Grafik können wir uns den Sachverhalt besser vorstellen.
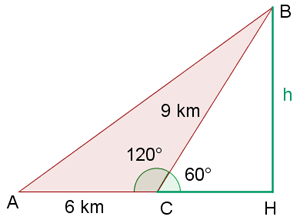
Um dieses Problem zu lösen, zeichnen wir zusätzliche Angaben ein. Wir müssen als Erstes die Katheten des rechtwinkligen Dreiecks (grün eingezeichnet) berechnen und können so dann die Katheten des anderen Dreiecks bestimmen sowie die Hypotenuse (unser gesuchter Wert).
Die Katheten des rechtwinkligen Dreiecks (grün) berechnen
Wir berechnen den Sinus und den Kosinus des Winkels Calcularemos el seno y el coseno del ángulo 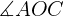 . Hierfür nehmen wir den Wert des Winkels und der Katheten sowie der Hypotenuse. So können wir schließlich die Katheten
. Hierfür nehmen wir den Wert des Winkels und der Katheten sowie der Hypotenuse. So können wir schließlich die Katheten  und
und  berechnen.
berechnen.

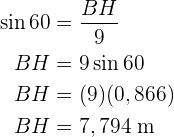
Die Katheten des anderen Dreiecks und die Hypotenuse berechnen
Zur Berechnung der Hypotenuse wenden wir den Satz von Pythagoras an. Die Katheten, die wir hierfür nutzen, sind  und
und 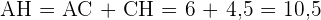 .
.

Mit KI zusammenfassen:



