Sinussatz
Jede Seite eines Dreiecks ist direkt proportional zum Sinus des gegenüberliegenden Winkels.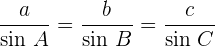
Anwendungen
Mit diesem Satz können Probleme gelöst werden, wenn die gegebenen Daten unter einen der folgenden Fälle fallen:
1 Wenn wir die Maße von 2 Seiten eines Dreiecks und den Winkel gegenüber einer der Seiten haben.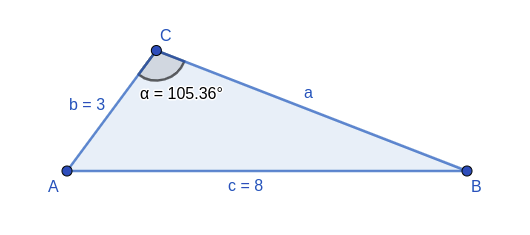
Durch die Anwendung des Satzes können wir sofort den Winkel ermitteln, der der anderen Seite, die uns bekannt ist, gegenüberliegt
2 Wenn wir die Maße von 2 Winkeln eines Dreiecks und der Seite, die einem von ihnen gegenüberliegt, haben.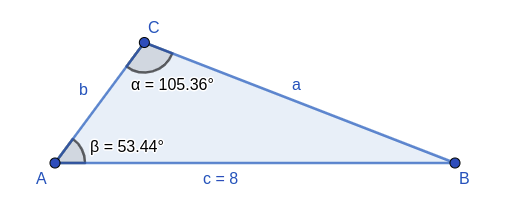
Wenn wir den Satz anwenden, können wir sofort die Gegenseite des anderen Winkels, der uns bekannt ist, bestimmen.
3 Wir können den Satz ebenfalls anwenden, wenn 2 Winkels des Dreiecks und eine Seite, die keinem der Winkel gegenüberliegt, bekannt sind. Hierbei ist nur ein zusätzlicher Schritt erforderlich, nämlich die Ermittllung des anderen Winkels des Dreiecks.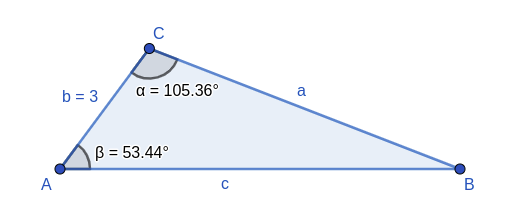
Dies ist möglich, weil wir wissen, dass die Summe der Winkel eines Dreiecks 180° beträgt.
Im obigen Bild zum Beispiel erhält man den Winkel B, indem man die beiden anderen Winkel von 180 subtrahiert:
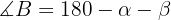
Wenn man einen der ursprünglich gegebenen Winkel ignoriert, hat man bereits die Angaben für 2 Winkel und die gegenüberliegende Seite eines dieser Winkel, wie im 2. in den Anwendungen genannten Fall.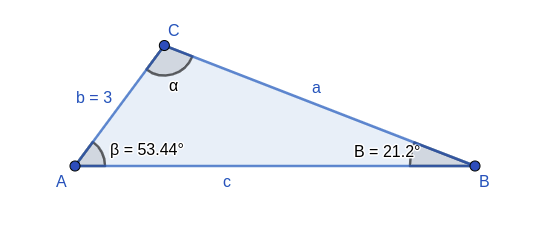
Kosinussatz
Bei einem Dreieck ist das Quadrat jeder Seite gleich der Summe der anderen Seiten zum Quadrat, minus zweimal das Produkt aus den beiden Seiten und dem Kosinus des Winkels, den sie bilden.
Anwendungen
Mit diesem Satz können folgende Probleme gelöst werden
1 Wenn wir die Maße eines Winkels und der an ihn angrenzenden Seiten haben.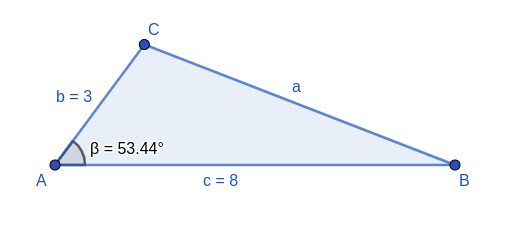
Wenn wir den Satz anwenden, können wir die 3. Seite ermitteln, also die dem Winkels gegenüberliegende Seite: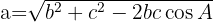
2 Wenn wir die Maße der 3 Seiten eines Dreiecks haben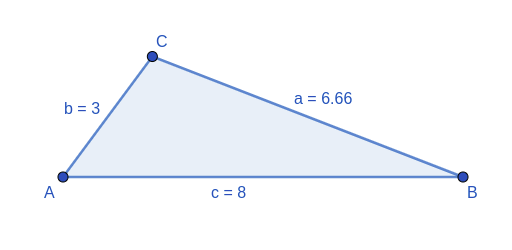
Mit dem Satz können wir einen beliebigen Winkel berechnen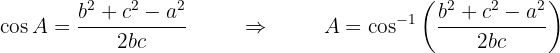
Tangenssatz
Der Tangenssatz stellt eine Beziehung zwischen zwei Seiten eines Dreiecks und ihren jeweiligen gegenüberliegenden Winkeln her.
Anwendungen:
Dieser Satz ist genauso nützlich wie der Sinus- und Kosinussatz, aber er ist weniger bekannt. Er kann in jedem der folgenden Fälle verwendet werden:
1 Zwei Seiten und ein gegenüberliegender Winkel sind bekannt.
2 Zwei Winkel und eine gegenüberliegende Seite sind bekannt.
Fläche eines Dreiecks
1 Die Fläche 
eines Dreiecks ist die Hälfte des Produkts aus der Basis und der dazugehörigen Höhe.
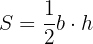
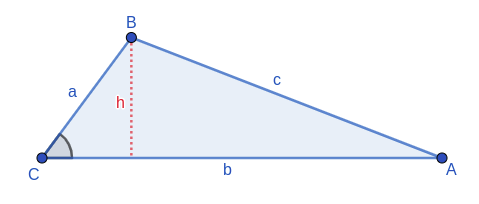
Laut Definition: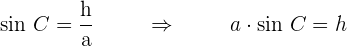 
Indem wir 
in die vorhergehende Flächenformel einsetzen, erhalten wir das folgende Ergebnis.
2 Der Flächeninhalt eines Dreiecks ist das halbe Produkt aus zwei seiner Seiten und dem Sinus des Winkels, den sie bilden.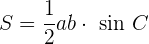
3 Der Flächeninhalt eines Dreiecks ist der Quotient aus dem Produkt seiner Seiten und dem Vierfachen des Radius seines Umkreises.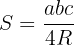
4 Der Flächeninhalt eines Dreiecks ist gleich dem Produkt aus dem Radius 
des Inkreises und seinem halben Umfang 
.
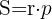
5 Satz des Heron: Wenn der halbe Umfang des Dreiecks ist, gilt
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
