Überprüfe die folgenden Identitäten:
A 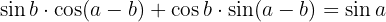
B 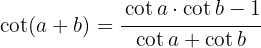
Überprüfe die folgenden Identitäten:
A 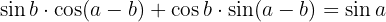
1 Wir wenden 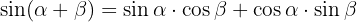 an
an
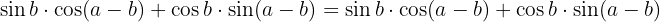
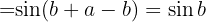
B 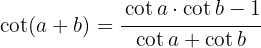
1 Wir schreiben den Kotangens als 
2 Wir wenden 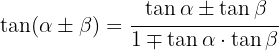 an
an
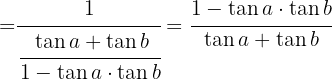
3 Wir dividieren den Zähler und den Nenner durch 
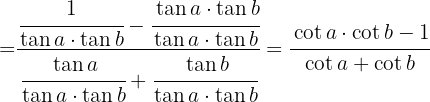
Vereinfache die Brüche
A 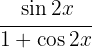
B 
C 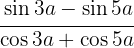
Vereinfache die Brüche:
A 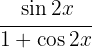 Wir wenden die Identitäten des doppelten Winkels an:
Wir wenden die Identitäten des doppelten Winkels an:
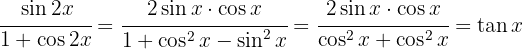
B  Im Zähler wenden wir eine Identität des Doppelwinkels und im Nenner eine Identität des Pythagoras an
Im Zähler wenden wir eine Identität des Doppelwinkels und im Nenner eine Identität des Pythagoras an
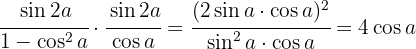
C 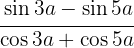 Wir verwenden Identitäten von Summe oder Differenz zum Produkt
Wir verwenden Identitäten von Summe oder Differenz zum Produkt
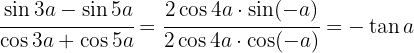
Berechne den Sinus und den Kosinus von 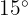 (ausgehend von
(ausgehend von 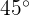 und
und  ).
).
Berechne den Sinus und den Kosinus von 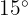 (ausgehend von
(ausgehend von 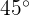 und
und  ).
).
A Für den Sinus drücken wir den Winkel als Differenz aus:
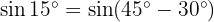
B Wir wenden die Identität des Sinus einer Differenz an:
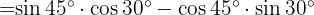

D Für den Kosinus führen wir die gleichen Schritte durch, wenden aber die Kosinusidentität einer Differenz an:
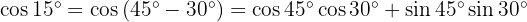
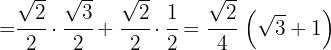
Berechne 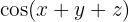
Berechne 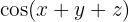
Wir führen ein Gruppierungszeichen ein und wenden die Kosinusidentität einer Winkelsumme an

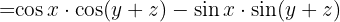
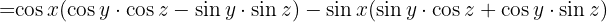
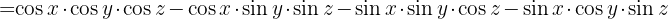
Löse die folgenden trigonometrischen Gleichungen:
A 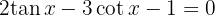
B 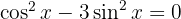
Löse die folgenden trigonometrischen Gleichungen:
A 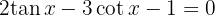
1 Wir ändern  in seine Umkehrfunktion und multiplizieren alles mit
in seine Umkehrfunktion und multiplizieren alles mit  :
:

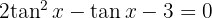
2 Wir substituieren 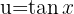 und lösen die resultierende quadratische Gleichung:
und lösen die resultierende quadratische Gleichung: 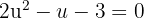
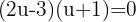

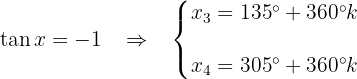
3 Wir machen Substitution rückgängig und erhalten die Werte von 
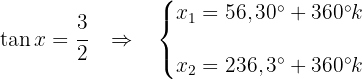
B 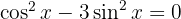
Wir wenden eine pythagoreische Identität an, um die Gleichung mit Sinus auszudrücken:
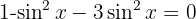
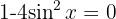
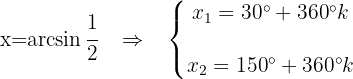

Löse die folgenden trigonometrischen Gleichungen:
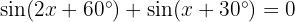

Löse die folgenden trigonometrischen Gleichungen:
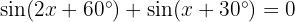
1 Wir wenden die Identität des doppelten Winkels für den Sinus an


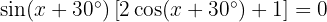
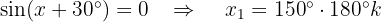



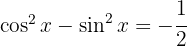
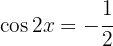
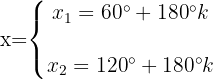
Löse die folgenden trigonometrischen Gleichungen:
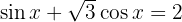
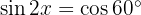
Löse die folgenden trigonometrischen Gleichungen:
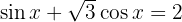

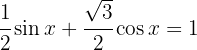
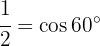 und
und 
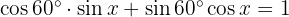

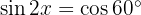
 auf
auf 

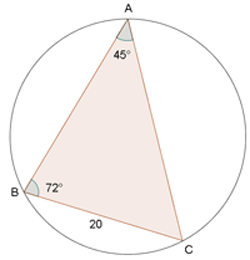
Berechne den Radius des Umkreises eines Dreiecks, wobei 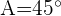 ,
, 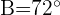 und
und 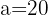 m.
m.
Berechne den Radius des Umkreises eines Dreiecks, wobei 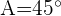 ,
, 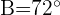 und
und 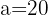 m.
m.
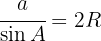
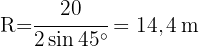
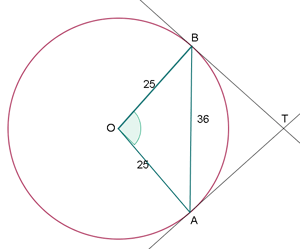
Der Radius eines Kreises beträgt  m. Berechne den Winkel, den die Tangenten an diesen Kreis bilden, die durch die Enden einer Sehne der Länge
m. Berechne den Winkel, den die Tangenten an diesen Kreis bilden, die durch die Enden einer Sehne der Länge  m gezogen werden.
m gezogen werden.
Der Radius eines Kreises beträgt  m. Berechne den Winkel, den die Tangenten an diesen Kreis bilden, die durch die Enden einer Sehne der Länge
m. Berechne den Winkel, den die Tangenten an diesen Kreis bilden, die durch die Enden einer Sehne der Länge  m gezogen werden.
m gezogen werden.
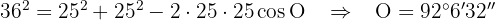
In einem Viereck 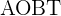 sind die Winkel
sind die Winkel  und
und  rechte Winkel.
rechte Winkel.

Mit KI zusammenfassen:


