In diesem Artikel findest du eine Reihe von Aufgaben, die mithilfe der Trigonometrie gelöst werden sollen. Unter den Lösungen zu jeder Aufgabe sind alle Rechenschritte im Einzelnen beschrieben.
Bringe die Gradmaße von Bogenmaß in Gradmaß
Die Formel für die Umrechnung eines Winkels im Bogenmaß in Grad lautet wie folgt

Dabei ist  der Winkel im Bogenmaß. In Grad sind die Winkel daher:
der Winkel im Bogenmaß. In Grad sind die Winkel daher:
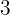 Hier ist
Hier ist 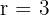 Das Gradmaß ist daher
Das Gradmaß ist daher 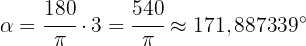 Um die Winkelminuten zu erhalten, multiplizieren wir die Dezimalstellen mit 60:
Um die Winkelminuten zu erhalten, multiplizieren wir die Dezimalstellen mit 60: 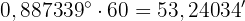 Um die Winkelsekunden zu erhalten, multiplizieren wir die Dezimalstellen erneut mit 60:
Um die Winkelsekunden zu erhalten, multiplizieren wir die Dezimalstellen erneut mit 60: 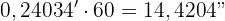 Daher lautet der Winkel in Gradzahlen
Daher lautet der Winkel in Gradzahlen 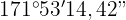
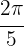 Wie im vorherigen Beispiel, verwenden wir auch hier die Formel
Wie im vorherigen Beispiel, verwenden wir auch hier die Formel 
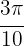 Auch hier verwenden wir dieselbe Formel:
Auch hier verwenden wir dieselbe Formel: 
Gib die folgenden Winkel im Bogenmaß an:
Die Formel für die Umwandlung von Gradmaß in Bogenmaß ist der vorherigen sehr ähnlich:
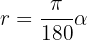
Die Winkel sind:
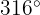 Verwende die Formel
Verwende die Formel 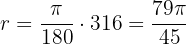 Der Winkel misst im Bogenmaß daher
Der Winkel misst im Bogenmaß daher 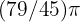 .
.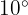 Verwende die Formel
Verwende die Formel 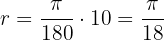 Der Winkel misst im Bogenmaß daher
Der Winkel misst im Bogenmaß daher 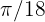 .
. Verwende die Formel
Verwende die Formel  Hier kann nichts vereinfacht werden, da 127 eine Primzahl ist. Der Winkel misst im Bogenmaß daher
Hier kann nichts vereinfacht werden, da 127 eine Primzahl ist. Der Winkel misst im Bogenmaß daher 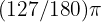 .
.
Gegeben ist 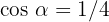 und
und  270^{\circ} < \alpha < 360^{\circ}[/latex]. Berechne die übrigen trigonometrischen Beziehungen für den Winkel [latex]\alpha[/latex].
270^{\circ} < \alpha < 360^{\circ}[/latex]. Berechne die übrigen trigonometrischen Beziehungen für den Winkel [latex]\alpha[/latex].
Wir wissen, dass der Winkel im vierten Quadranten des Koordinatensystems liegt. Für diesen Quadranten gilt  , aber
, aber  . Folglich ist
. Folglich ist
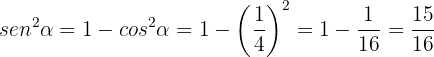
Daraus erhält man
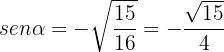
Da wir  und
und  schon bestimmt haben, sind die anderen Beziehungen einfacher zu ermitteln.
schon bestimmt haben, sind die anderen Beziehungen einfacher zu ermitteln.

Man kann sowohl das Ergebnis des Kotangens als auch des Kosekans rationalisieren. Daher wäre ebenso korrekt:
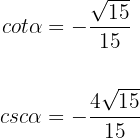
Das Ergebnis erhalten wir, wenn wir die vorherigen Ergebnisse mit  multiplizieren. Somit vermeiden wir, dass Wurzeln im Nenner auftreten.
multiplizieren. Somit vermeiden wir, dass Wurzeln im Nenner auftreten.
Gegeben ist 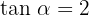 und
und  180^{\circ} < \alpha < 270^{\circ}[/latex]. Berechne die übrigen trigonometrischen Beziehungen für den Winkel [latex]\alpha[/latex].
180^{\circ} < \alpha < 270^{\circ}[/latex]. Berechne die übrigen trigonometrischen Beziehungen für den Winkel [latex]\alpha[/latex].
Der Winkel  liegt im dritten Quadranten des Koordinatensystems. Daher wissen wird, dass
liegt im dritten Quadranten des Koordinatensystems. Daher wissen wird, dass 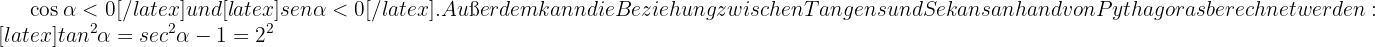
Daraus ergibt sich

Da 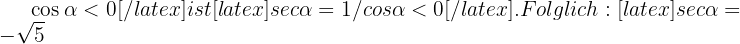
Daraus erhält man

Man kann erkennen, dass 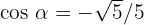 auch eine korrekte Antwort wäre, wenn man das vorherige Ergebnis rationalisiert.
auch eine korrekte Antwort wäre, wenn man das vorherige Ergebnis rationalisiert.
Wir wissen auch, dass  . Daraus ergibt sich
. Daraus ergibt sich

Die übrigen beiden Beziehungen können nun einfacher ermittelt werden:

und

Gegeben sind 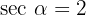 und
und  0 < \alpha < \pi /2[/latex]. Berechne die übrigen trigonometrischen Beziehungen für den Winkel [latex]\alpha[/latex].
0 < \alpha < \pi /2[/latex]. Berechne die übrigen trigonometrischen Beziehungen für den Winkel [latex]\alpha[/latex].
Der Winkel liegt im Bogenmaß vor. Außerdem liegt er im ersten Quadranten des Koordinatensystems, daher ist 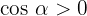 und
und  .
.
Die Beziehung von Sekans und  kann über Pythagoras berechnet werden:
kann über Pythagoras berechnet werden:
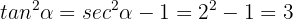
Außerdem ist 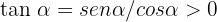 , da
, da  und
und  . Folglich:
. Folglich:
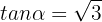
Ebenso ist
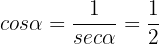
Da  ist, können wir schließen, dass
ist, können wir schließen, dass
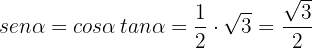
Die übrigen beiden Beziehungen können nun einfacher ermittelt werden:
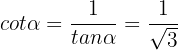
und

Berechne den Sinus, Kosinus und Tangens für die folgenden Winkel:
Wir gehen davon aus, dass Sinus und Kosinus der bekanntesten Winkelmaße (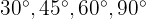 , etc.) bereits bekannt sind:
, etc.) bereits bekannt sind:
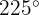 Um den Sinus des Winkels zu berechnen, machen wir uns die Eigenschaften zur Verschiebung von Sinus- und Kosinusfunktionen zunutze. Wir können erkennen, dass
Um den Sinus des Winkels zu berechnen, machen wir uns die Eigenschaften zur Verschiebung von Sinus- und Kosinusfunktionen zunutze. Wir können erkennen, dass 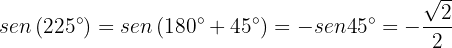 Ähnlich ist,
Ähnlich ist,  Zuletzt ist
Zuletzt ist 
 Wie im vorherigen Fall machen wir uns die Eigenschaften zur Verschiebung von Sinus- und Kosinusfunktionen zunutze. Wir können erkennen, dass
Wie im vorherigen Fall machen wir uns die Eigenschaften zur Verschiebung von Sinus- und Kosinusfunktionen zunutze. Wir können erkennen, dass 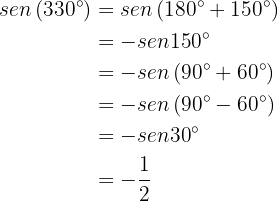 Ähnlich ist,
Ähnlich ist, 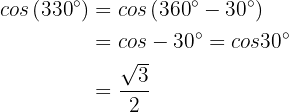 Zuletzt ist
Zuletzt ist 
Ermittle die trigonometrischen Beziehungen der folgenden Winkel:
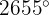 Zuerst müssen wir einen Winkel finden, der zwischen
Zuerst müssen wir einen Winkel finden, der zwischen  und
und 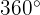 liegt und gleich
liegt und gleich 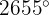 ist. Dafür teilen wir 2655 durch 360. Der Rest ist der gesuchte Winkel:
ist. Dafür teilen wir 2655 durch 360. Der Rest ist der gesuchte Winkel:  , wobei der Rest 135 ist. Daher ist
, wobei der Rest 135 ist. Daher ist 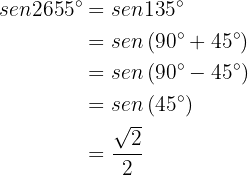 Ähnlich ist
Ähnlich ist 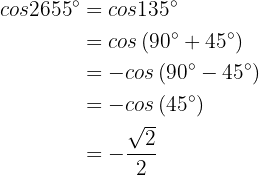 Zuletzt ist
Zuletzt ist 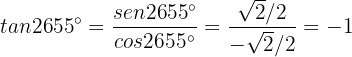
 In diesem Fall verhält es sich ähnlich: Wir teilen zuerst 840 durch 360 und verwenden den Rest:
In diesem Fall verhält es sich ähnlich: Wir teilen zuerst 840 durch 360 und verwenden den Rest: 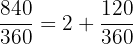 Daher ist
Daher ist 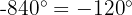 . Folglich:
. Folglich: 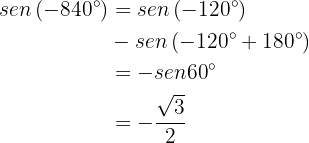 Ähnlich ist,
Ähnlich ist, 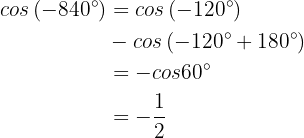 Zuletzt ist
Zuletzt ist 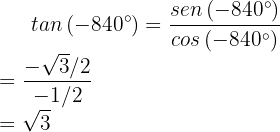
Gegeben sei das rechtwinklige Dreieck ABC, dessen rechter Winkel bei  liegt. Wir wissen, dass
liegt. Wir wissen, dass  und
und 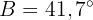 misst. Berechne die beiden anderen Winkel und Seitenlängen.
misst. Berechne die beiden anderen Winkel und Seitenlängen.
Sieh dir die Skizze des Dreiecks an:
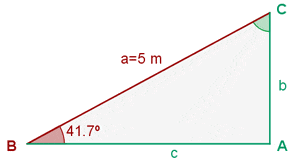
Hier kannst du die noch fehlenden Maße erkennen (die Seiten  ,
,  und der Winkel
und der Winkel  ). Am einfachsten lässt sich der Winkel
). Am einfachsten lässt sich der Winkel  berechnen, da
berechnen, da  ist. Daher ist
ist. Daher ist
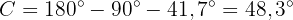
Da das Dreieck rechtwinklig ist, können wir trigonometrische Funktionen anwenden, um die Längen der übrigen Seiten zu bestimmen. Wir wissen, dass

Daher ist
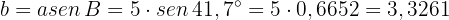
Da  , ist folglich
, ist folglich
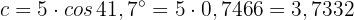
Damit haben wir alle fehlenden Maße gefunden.
Gegeben sei das rechtwinklige Dreieck ABC, dessen rechter Winkel bei  liegt. Wir wissen, dass
liegt. Wir wissen, dass 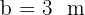 und
und 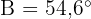 misst. Berechne die beiden anderen Winkel und Seitenlängen.
misst. Berechne die beiden anderen Winkel und Seitenlängen.
Sieh dir die Skizze des Dreiecks an:
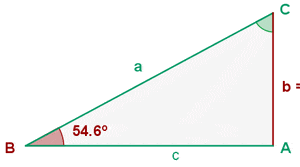
Hier kannst du die noch fehlenden Angaben sehen (die Seiten  ,
,  und der Winkel
und der Winkel  ). Wie im vorherigen Beispiel lässt sich der Winkel bei
). Wie im vorherigen Beispiel lässt sich der Winkel bei  am einfachsten berechnen, da
am einfachsten berechnen, da  . Daher ist
. Daher ist
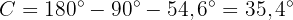
Dieses Mal liegt die Hypotenuse nicht vor. Daher müssen wir den Tangens verwenden:
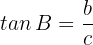
Daher ist
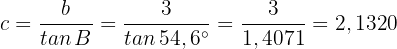
Da  , ist folglich
, ist folglich
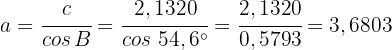
Damit haben wir alle fehlenden Maße gefunden.
Gegeben sei das rechtwinklige Dreieck ABC, dessen rechter Winkel bei  liegt. Wir wissen, dass
liegt. Wir wissen, dass  und
und 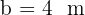 misst. Berechne den spitzen Winkel und die fehlende Seitenlänge.
misst. Berechne den spitzen Winkel und die fehlende Seitenlänge.
Sieh dir die Skizze des Dreiecks an:
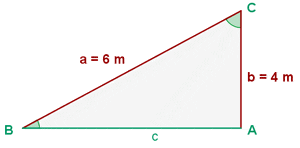
Gescuht sind die Kathete  und die Winkel
und die Winkel  und
und  . Nach Pythagoras wissen wir, dass
. Nach Pythagoras wissen wir, dass  . Daher ist
. Daher ist
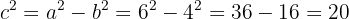
Folglich ist 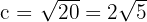 . Außerdem ist
. Außerdem ist
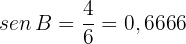
Daher ist 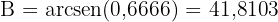 . Da die Winkelsumme
. Da die Winkelsumme  ergibt, ist:
ergibt, ist:
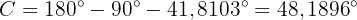
Damit haben wir alle fehlenden Maße gefunden.
Gegeben sei das rechtwinklige Dreieck ABC. Wir wissen, dass 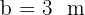 ,
,  und
und 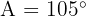 misst. Ermittle die Winkel und die fehlenden Seiten.
misst. Ermittle die Winkel und die fehlenden Seiten.
Diesmal ist das Dreieck nicht rechtwinklig. Sieh dir das Dreieck auf der Skizze an:
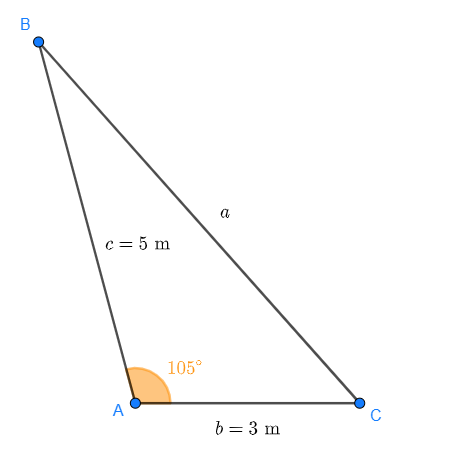
Es fehlen noch die Winkel  ,
,  und die Seite
und die Seite  . Da das Dreieck nicht rechtwinklig ist, können wir des Satz des Pythagoras nicht anwenden. Den Kosinussatz allerdings schon:
. Da das Dreieck nicht rechtwinklig ist, können wir des Satz des Pythagoras nicht anwenden. Den Kosinussatz allerdings schon:

Dort sind alle Maße enthalten. Wir haben
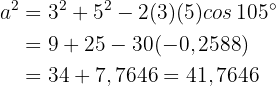
Daher ist 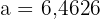 . Mithilfe des Sinussatzes können wir nun alle weiteren Winkel berechnen:
. Mithilfe des Sinussatzes können wir nun alle weiteren Winkel berechnen:

Daraus ergibt sich
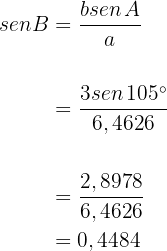
Daher ist 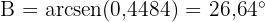 .
.
Zuletzt ist
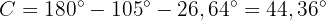
Somit haben wir alle Maße des Dreiecks bestimmt.
Ein 50 Meter hoher Baum wirft einen 60 Meter langen Schatten. Ermittle den Winkel, in dem die Sonne in diesem Moment steht.
Der Baum (Seite  ) und der Schatten (Seite
) und der Schatten (Seite  ) bilden das folgende Dreieck:
) bilden das folgende Dreieck:
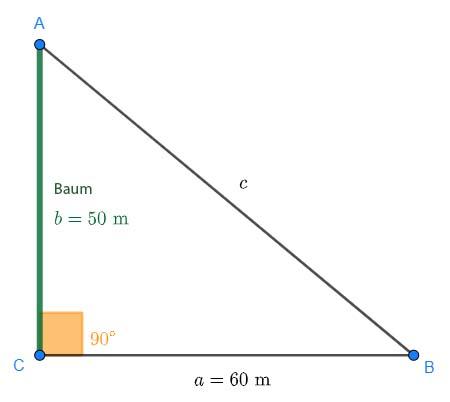
Wir sehen, dass die Seite  nicht berechnet werden muss. Wir suchen den Winkel
nicht berechnet werden muss. Wir suchen den Winkel  , dessen Tangens wie folgt gegeben ist:
, dessen Tangens wie folgt gegeben ist:
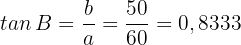
Mithilfe des Arcotangens erhalten wir
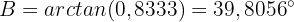
Wir haben den gesuchten Winkel gefunden.
Eine Drohne fliegt in einer Höhe von 800 Metern. Sie filmt ein Dorf mit einem Vertiefungswinkel von 12°. Wie weit muss die Drohne in gerader Linie unter Beibehaltung seiner Höhe fliegen, um genau über dem Dorf zu sein?
Zwischen dem Dorf und der Drohne liegt das folgende Dreieck:
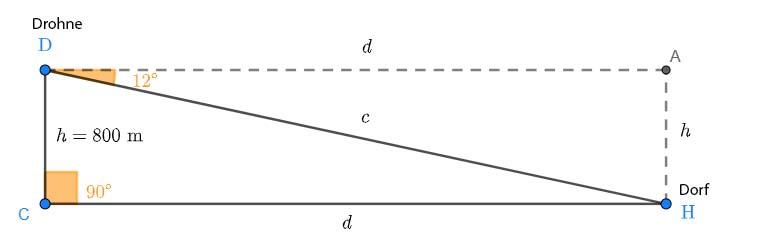
Wir benennen die unbekannte Strecke mit  . Die Höhe, in der die Drohne fliegt, bezeichnen wir mit
. Die Höhe, in der die Drohne fliegt, bezeichnen wir mit  . Der Vertiefungswinkel stimmt mit dem Winkel
. Der Vertiefungswinkel stimmt mit dem Winkel 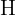 überein.
überein.
Der Tangens von 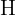 kann wie folgt berechnet werden:
kann wie folgt berechnet werden:

Daher ist
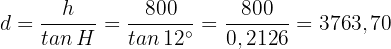
Die Drohne muss also 3763,70 Meter (bzw. 3,764 km) fliegen.
Ermittle den Radius eines Kreises mit einer Kreissehne von 24,6 Metern und einem Kreisbogen von 70°.
Sieh dir die Skizze an:
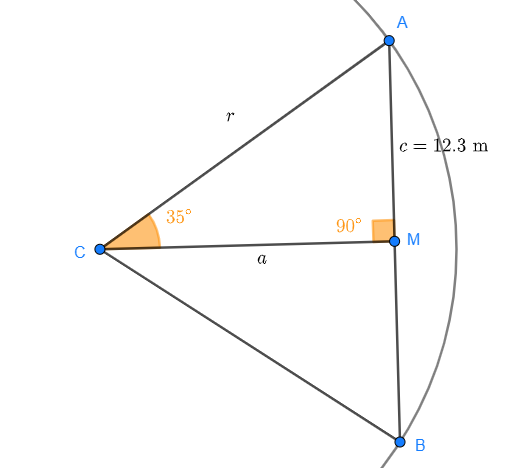
Wir können sehen, dass ein rechtwinkliges Dreieck mit den Punkten  entsteht, in dem
entsteht, in dem  der Mittelpunkt des Kreisbogens ist.
der Mittelpunkt des Kreisbogens ist.
Der Radius  ist die Hypotenuse des Dreiecks. Die Länge von
ist die Hypotenuse des Dreiecks. Die Länge von  ist die Hälfte der Kreissehne, das heißt,
ist die Hälfte der Kreissehne, das heißt,
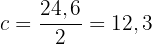
und der Winkel  misst
misst  (die Hälfte des Kreisbogens). Wir wissen, dass
(die Hälfte des Kreisbogens). Wir wissen, dass
 ,
,
da  die Hypotenuse ist. Folglich ist
die Hypotenuse ist. Folglich ist
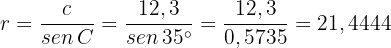
Daher misst der Radius 21,44 Meter.
erechne den Flächeninhalt eines Dreiecks mit den beiden Seitenlängen 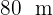 und
und 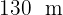 , die einen Winkel von 70° einschließen.
, die einen Winkel von 70° einschließen.
Diese Aufgabe kann über mehrere Wege gelöst werden. Wir können dafür die Heronsche Flächenformel verwenden oder versuchen, die Höhenmaße herauszufinden. Sieh dir zuerst die Skizze des Dreiecks an:
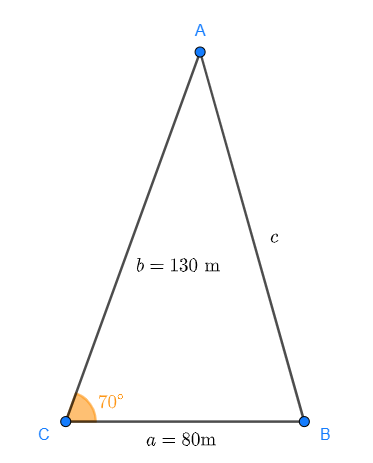
Darin sind 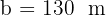 ,
, 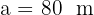 und
und 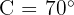 .
.
Wenn wir senkrecht zu  die Höhe einzeichnen, bildet sich ein rechtwinkliges Dreieck, in dem
die Höhe einzeichnen, bildet sich ein rechtwinkliges Dreieck, in dem  die Kathete ist und
die Kathete ist und  die Hypotenuse. Außerdem ist der Sinus von
die Hypotenuse. Außerdem ist der Sinus von 
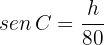
Daher ist
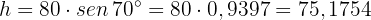
Die Fläche misst also
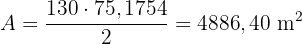
Berechne die Höhe eine Baumes. Von einem Punkt aus der Umgebung aus kann man seine Krone aus einem Winkel von 30° über der Erde betrachten. Wenn man sich ihm 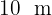 nähert, betrachtet man seine Krone aus einem Winkel von 60° über der Erde.
nähert, betrachtet man seine Krone aus einem Winkel von 60° über der Erde.
Sieh dir die Skizze an zur Aufgabenstellung an:
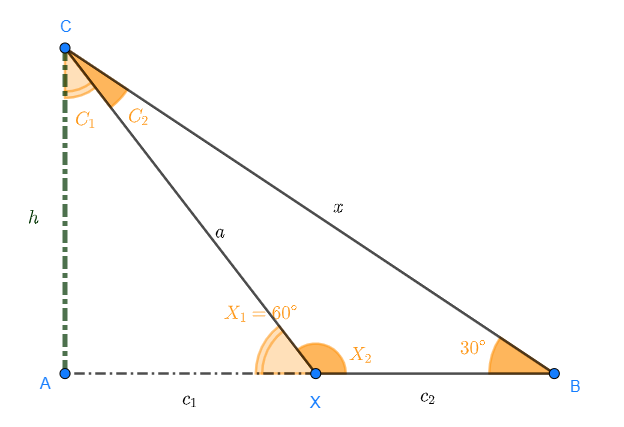
Diese Aufgabe kann über mehrere Wege gelöst werden. Eine Möglichkeit ist es, die Strecke 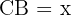 des Dreiecks
des Dreiecks  zu berechnen; anschließend verwenden wir die Strecke, um die Höhe herauszufinden.
zu berechnen; anschließend verwenden wir die Strecke, um die Höhe herauszufinden.
Für die Berechnung des Dreiecks wissen wir, dass der Winkel 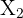 des Dreiecks
des Dreiecks 
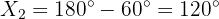 ist.
ist.
Daher können wir nun den Sinussatz verwenden. Zuerst benötigen wir aber den Winkel 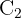 :
:

Nach Sinussatz erhalten wir
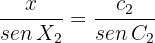
Dabei ist
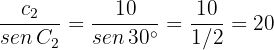
Daher ist
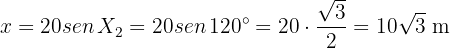
Jetzt können wir die Höhe berechnen. Wir können erkennen, dass das Dreieck  rechtwinklig ist. Folglich ist
rechtwinklig ist. Folglich ist
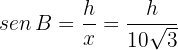
Folglich ist
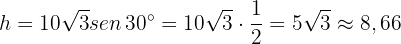
Der Baum ist also 8,66 Meter hoch.
Ein regelmäßiges Achteck hat eine Seitenlänge von 12 Metern. Ermittle die Radien des Inkreises und des Umkreises.
Sie dir das Achteck in der Skizze an:
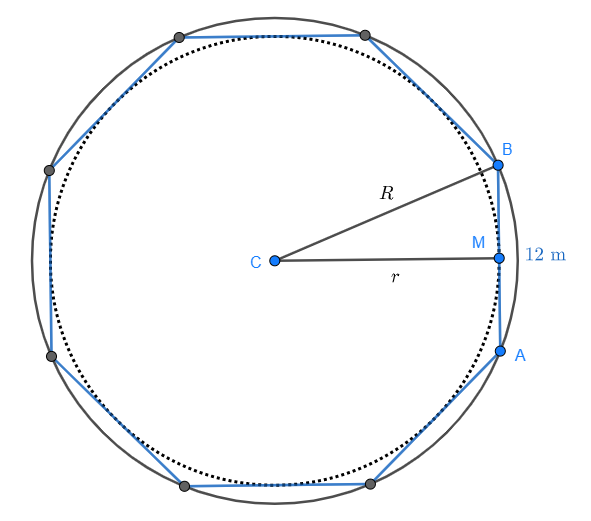
Zwischen den Punkten  bildet sich ein rechtwinkliges Dreieck, dessen Punkt
bildet sich ein rechtwinkliges Dreieck, dessen Punkt  der Mittelpunkt zu jeder Seite des Achtecks ist. Sieh dir das rechtwinklige Dreieck im Detail an:
der Mittelpunkt zu jeder Seite des Achtecks ist. Sieh dir das rechtwinklige Dreieck im Detail an:
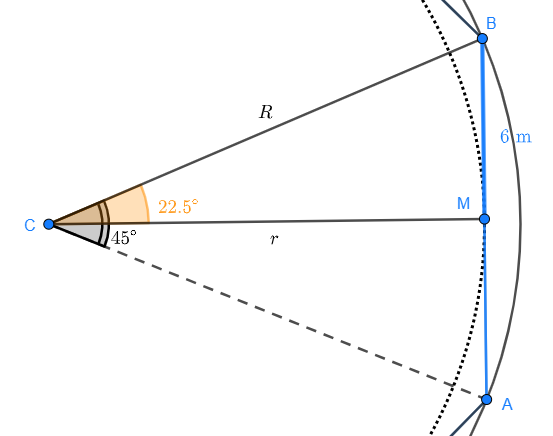
Wir wissen, dass der Winkel 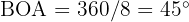 hat. Der Winkel
hat. Der Winkel  des rechtwinkligen Dreiecks hat also
des rechtwinkligen Dreiecks hat also 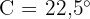 . Außerdem ist die Seite
. Außerdem ist die Seite 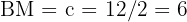 .
.
Die beiden noch fehlenden Seiten sind gleich dem Radius des In- bzw. Umkreises. Für Seite  erhalten wir
erhalten wir

Wir erhalten
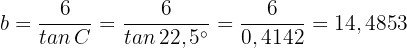
Der Radius  des Inkreises misst also 14,49 Meter.
des Inkreises misst also 14,49 Meter.
Die Seite  erfüllt
erfüllt
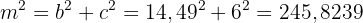
Somit ist 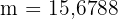 . D.h. der Radius
. D.h. der Radius  des Umkreises beträgt 15,68 Meter.
des Umkreises beträgt 15,68 Meter.
Drei Städte 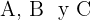 liegen dreiecksförmig nebeneinander und werden durch geradlinige Wege verbunden. Wenn die Strecke von
liegen dreiecksförmig nebeneinander und werden durch geradlinige Wege verbunden. Wenn die Strecke von  nach
nach  12 km beträgt, beträgt die Strecke von
12 km beträgt, beträgt die Strecke von  nach
nach  10 km und der Winkel
10 km und der Winkel 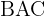 hat
hat 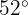 . Ermittle den Abstand zwischen den Städten
. Ermittle den Abstand zwischen den Städten 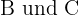 .
.
Sieh dir das Dreieck in der Skizze an:
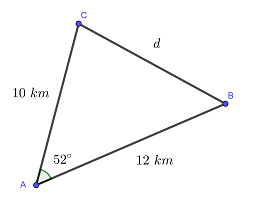
Um die Seite  zu berechnen, kann der Kosinussatz angewendet werden:
zu berechnen, kann der Kosinussatz angewendet werden:

Führe die Rechnung weiter und du erhältst
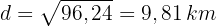
Somit haben wir den Anbstand zwischen den Städten 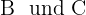 gefunden.
gefunden.
Peter lässt einen Drachen mit einer 40 m langen Schnur steigen. Wenn der Steigungswinkel 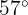 beträgt, wie hoch fliegt der Drache über dem Boden?
beträgt, wie hoch fliegt der Drache über dem Boden?
Die Schnur des Drachen (Seite  ) und die Höhe des Drachen über dem Boden (Seite
) und die Höhe des Drachen über dem Boden (Seite  ) bilden ein rechtwinkliges Dreieck:
) bilden ein rechtwinkliges Dreieck:
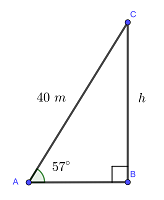
Der Sinus des Winkels  kann wie folgt ausgedrückt werden:
kann wie folgt ausgedrückt werden:
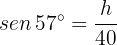
Wir stellen nach  um und erhalten
um und erhalten
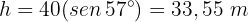
Die gesuchte Höhe ist damit gefunden.
Ein Gebäude wirft einen 60 m langen Schatten, wenn die Sonne in einem Winkel von 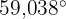 steht. Wie hoch ist das Gebäude?
steht. Wie hoch ist das Gebäude?
Das Gebäude (Seite  ) und der Schatten (Seite
) und der Schatten (Seite 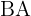 ) bilden das folgende rechtwinklige Dreieck:
) bilden das folgende rechtwinklige Dreieck:
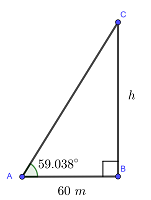
Der Tangens des Winkels 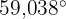 kann wie folgt ausgedrückt werden:
kann wie folgt ausgedrückt werden:
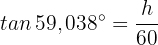
Wir stellen nach  um und erhalten
um und erhalten
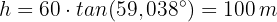
Die gesuchte Höhe ist damit gefunden.
Beweise die trigonometrische Gleichheit der folgenden Gleichungen:
 Schreibe zuerst
Schreibe zuerst 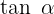 und
und 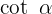 der Definition nach in Sinus und Kosinus um:
der Definition nach in Sinus und Kosinus um:  Bilde die Bruchsumme anhand des gemeinsamen Nenners:
Bilde die Bruchsumme anhand des gemeinsamen Nenners:  Wir sehen, dass
Wir sehen, dass 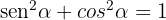 ist, daher ist
ist, daher ist 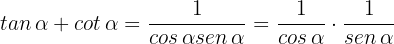 Dies sind Definitionen von
Dies sind Definitionen von  und
und  . Folglich ist
. Folglich ist 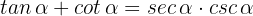
 Hier bietet es sich an, auf der rechten Seite der Gleichung zu beginnen:
Hier bietet es sich an, auf der rechten Seite der Gleichung zu beginnen:  Wir faktorisieren
Wir faktorisieren 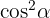
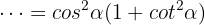 Aus
Aus 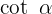 ergibt sich nach Pythagoras
ergibt sich nach Pythagoras 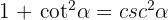 , daher erhalten wir
, daher erhalten wir 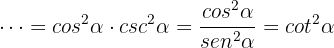 Somit ist die Aufgabe bewiesen.
Somit ist die Aufgabe bewiesen.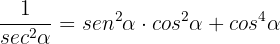 Hier bietet es sich an, auf der rechten Seite der Gleichung zu beginnen, indem man
Hier bietet es sich an, auf der rechten Seite der Gleichung zu beginnen, indem man 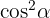 faktorisiert:
faktorisiert: 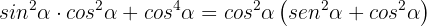 Wir sehen, dass
Wir sehen, dass 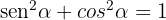 ist, daher ist
ist, daher ist 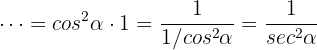 Somit ist die Aufgabe bewiesen.
Somit ist die Aufgabe bewiesen.
Beweise die trigonometrische Gleichheit der folgenden Gleichungen:
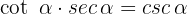 Hier ist es am Einfachsten, auf der linken Seite der Gleichung zu beginnen und die Beziehungen mit Sinus und Kosinus auszudrücken:
Hier ist es am Einfachsten, auf der linken Seite der Gleichung zu beginnen und die Beziehungen mit Sinus und Kosinus auszudrücken:  , da
, da  aufgehoben wird. Diese Aufgabe konnte in nur einem Schritt bewiesen werden.
aufgehoben wird. Diese Aufgabe konnte in nur einem Schritt bewiesen werden. Hier beginnen wir wieder auf der linken Seite und drücken die Beziehungen mit Sinus und Kosinus aus:
Hier beginnen wir wieder auf der linken Seite und drücken die Beziehungen mit Sinus und Kosinus aus: 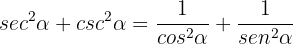 Wir bringen die Brüche auf einen gemeinsamen Nenner und summieren sie:
Wir bringen die Brüche auf einen gemeinsamen Nenner und summieren sie: 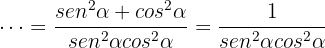 , da
, da 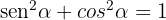 . Somit ist die Aufgabe bewiesen.
. Somit ist die Aufgabe bewiesen.
Mit KI zusammenfassen: