Kapitel
- Systeme zur Messung von Winkeln
- Trigonometrische Funktionen
- Trigonometrische Zusammenhänge am Einheitskreis
- Vorzeichen der trigonometrischen Funktionen
- Trigonometrische Zusammenhänge der 30º- und 60º-Winkel
- Trigonometrische Zusammenhänge des 45º-Winkels
- Tabelle der trigonometrischen Zusammenhänge mit den gängigsten Winkeln
- Grundlegende trigonometrische Zusammenhänge
- Komplementwinkel und Supplementwinkel
- Negative Winkel und Gegenwinkel
- Winkel, die sich um ein Vielfaches von 90º unterscheiden.
- Rechtwinklige Dreiecke lösen
Systeme zur Messung von Winkeln
Die folgenden Einheiten werden zur Messung von Winkeln verwendet:
1 Grad (°):
Wird der Kreis in 
gleiche Teile geteilt, so ist der Mittelpunktswinkel, der jedem dieser Teile entspricht, ein Winkel vom Grad 
.
Ein Grad hat 
Minuten (') und eine Minute hat Sekunden ('').
2 Radiant (rad):
Es ist das Maß eines Winkels, dessen Bogen einen Radius misst.
Trigonometrische Funktionen
1 Sinus
Sinus des Winkels 
: das Verhältnis zwischen der Gegenkathete des Winkels und der Hypotenuse.
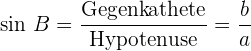
2 Kosinus
Kosinus des Winkels : das Verhältnis zwischen der angrenzenden Kathete (oder Ankathete) des Winkels und der Hypotenuse.
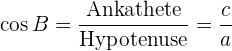
3 Tangens
Tangens des Winkels : das Verhältnis zwischen der Gegenkathete des Winkels und der angrenzenden Kathete des Winkels.
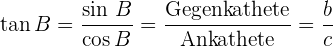
4 Kosekans
Kosekans des Winkels : das umgekehrte Verhältnis des Sinus von .
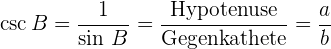
5 Sekans
Sekans des Winkels : das umgekehrte Verhältnis des Kosinus von .
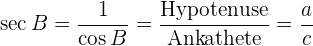
6 Kotangens
Kotangens des Winkels : das umgekehrte Verhältnis des Tangens von .
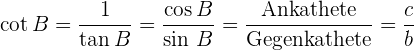
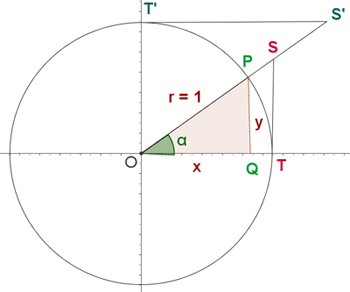
Trigonometrische Zusammenhänge am Einheitskreis
Der Einheitskreis ist der Kreis, dessen Mittelpunkt im Koordinatenursprung liegt und dessen Radius die Einheit ist. Im goniometrischen Kreis begrenzen die Koordinatenachsen vier Quadranten, die gegen den Uhrzeigersinn nummeriert sind, beginnend mit dem Quadranten, der durch die positiven Achsen begrenzt wird.
Der Sinus ist die Ordinate des Punktes 
. Außerdem: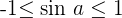 
Der Kosinus ist die Abszisse des Punktes . Außerdem: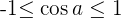 
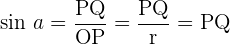
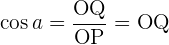
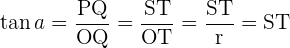
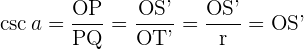
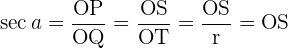
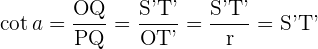
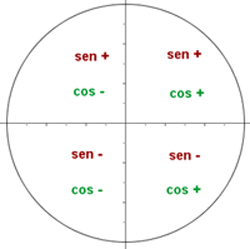
Vorzeichen der trigonometrischen Funktionen
Da der Sinus der Wert der Ordinate und der Kosinus der Wert der Abszisse des Punktes auf dem Einheitskreis ist, sind diese Werte je nach Quadrant negativ oder positiv. In den Quadranten I und II ist zum Beispiel die y-Achse positiv, sodass der Sinus dort positiv ist, da sein Wert der Ordinate entspricht. In den Quadranten III und IV ist er negativ. Beim Kosinus hingegen ist der Wert die Abszisse, und da die x-Achse in den Quadranten auf der rechten Seite positiv ist, ist der Kosinus in den Quadranten I und IV positiv und in II und III negativ.
Nachstehend findest du eine Tabelle mit den trigonometrischen Zusammenhängen an den Winkeln, die den Anfang bzw. das Ende eines jeden Quadranten markieren.
 | 0º | 90º | 180º | 270º |
|---|---|---|---|---|
| sin |  |  | |  |
| cos | | | | |
| tan | |  | |  |
Trigonometrische Zusammenhänge der 30º- und 60º-Winkel
Um die trigonometrischen Zusammenhänge der Winkel mit den Maßen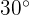 
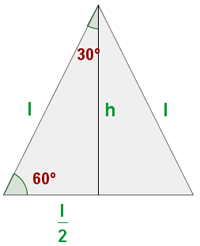
und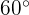 
zu analysieren, kann man sich die Hälfte eines gleichseitigen Dreiecks vorstellen:
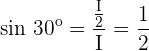
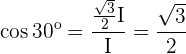
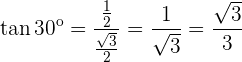
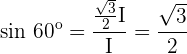
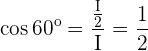
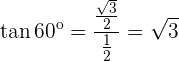
Trigonometrische Zusammenhänge des 45º-Winkels
Um die trigonometrischen Zusammenhänge des Winkels mit dem Maß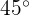 
zu analysieren, kann man sich ein durch die Diagonale geteiltes Quadrat vorstellen:
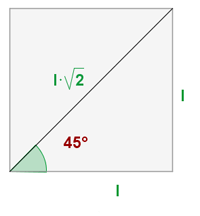
Mithilfe der Definitionen der trigonometrischen Zusammenhänge erhalten wir:
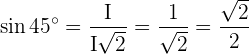
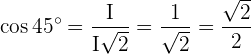
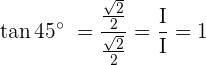
Tabelle der trigonometrischen Zusammenhänge mit den gängigsten Winkeln
| 0º | 30º | 45º | 60º | 90º | 180º | 270º |
|---|---|---|---|---|---|---|---|
| sin | |  |  |  | | | |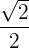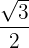
| cos | | | | | | | |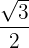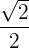
| tan | |  | |  | | | |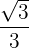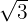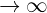
Grundlegende trigonometrische Zusammenhänge
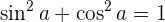
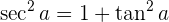
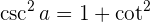
Komplementwinkel und Supplementwinkel
Komplementwinkel
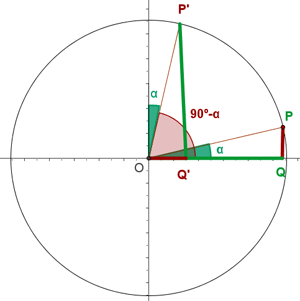
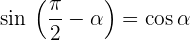
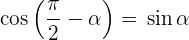
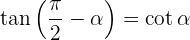
Supplementwinkel
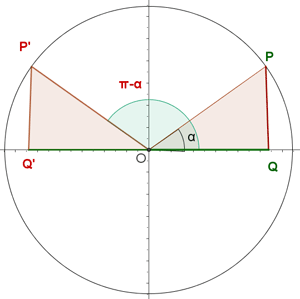
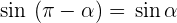
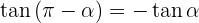
Negative Winkel und Gegenwinkel
Negative Winkel
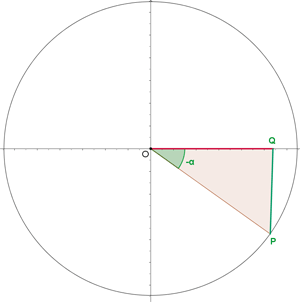
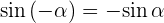
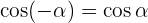
Gegenwinkel
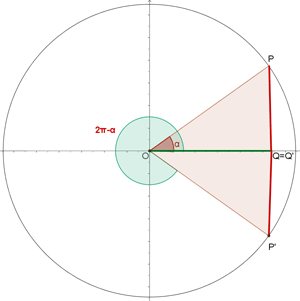
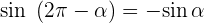
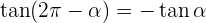
Winkel, die sich um ein Vielfaches von 90º unterscheiden.
Winkel, die sich um 90º oder π/2 rad unterscheiden
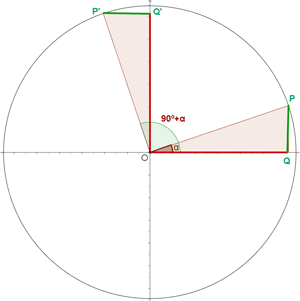
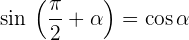
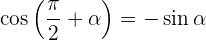
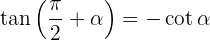
Winkel, die sich um 180° oder π rad unterscheiden
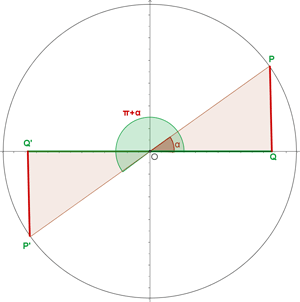
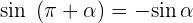
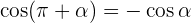
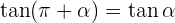
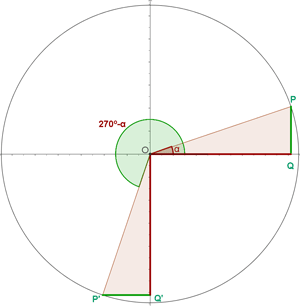
Winkel, die sich um 270º oder 3/2 π rad unterscheiden
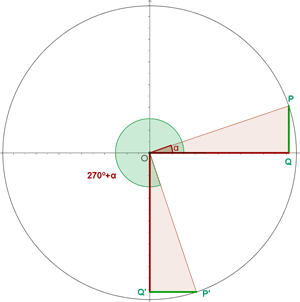
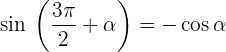
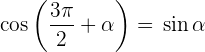
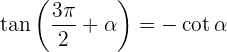
Winkel, die größer als 360º sind
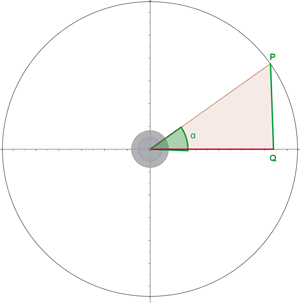
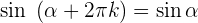
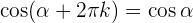
Winkel, die sich zu 270º oder 3/2 π rad addieren
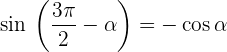
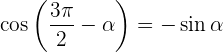
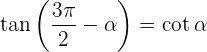
Rechtwinklige Dreiecke lösen
Fall 1: Die Hypotenuse und eine Kathete sind bekannt.
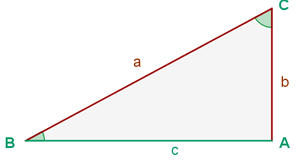
Fall 2: Die beiden Katheten sind bekannt.
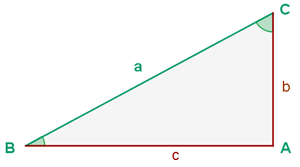
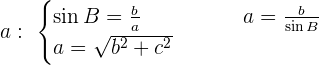
Fall 3: Die Hypotenuse und ein spitzer Winkel sind bekannt.
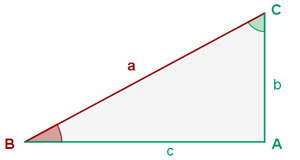
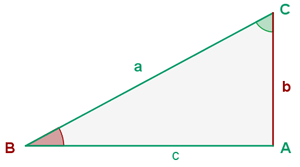
Fall 4: Eine Kathete und ein spitzer Winkel sind bekannt.
Du findest diesen Artikel toll? Vergib eine Note!
Loading...
