Kapitel

Was sind die trigonometrischen Gleichungen
Bei trigonometrischen Gleichungen handelt es sich um trigonometrische Funktionen, die periodisch sind und deren Lösungen daher in einem oder zwei Quadranten auftreten können und sich in allen Runden wiederholen.
Um eine trigonometrische Gleichung zu lösen, müssen wir die notwendigen Umformungen vornehmen, um mit einer einzelnen trigonometrischen Funktion zu arbeiten, indem wir die grundlegenden trigonometrischen Identitäten verwenden.
Beispiele für die Lösung von trigonometrischen Gleichungen
Löse die trigonometrischen Gleichungen:
1 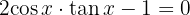
Beispiele für trigonometrische Gleichungen, bei denen verschiedene trigonometrische Identitäten zur Lösung verwendet werden
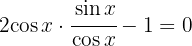
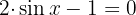
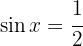


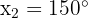
Die allgemeine Formel:
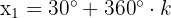

mit 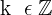
2 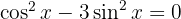 für
für 
Aus dem trigonometrischen Pythagoras des Sinus und des Kosinus 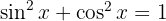 können wir ableiten, dass
können wir ableiten, dass 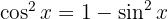 , weshalb die Gleichung wie folgt umgeschrieben werden kann:
, weshalb die Gleichung wie folgt umgeschrieben werden kann:

Wir gruppieren ähnliche Terme und ermitteln 
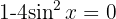
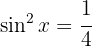
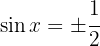
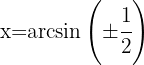

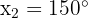
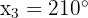
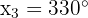
3 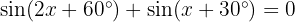
Wir wandeln die Summe in ein Produkt um
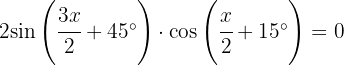
Wir dividieren auf beiden Seiten durch 2 und setzen jeden Faktor gleich 0.
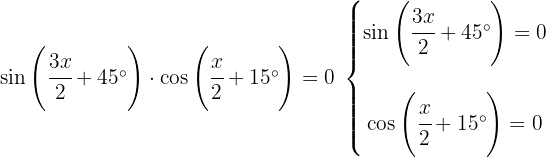
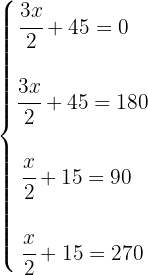

con 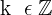
4 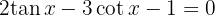
Wir multiplizieren beide Glieder der Gleichung mit 
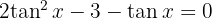

Wir faktorisieren das 1. Glied als quadratisches Trionom der Form 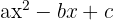 und setzen jeden Faktor gleich 0
und setzen jeden Faktor gleich 0
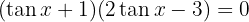
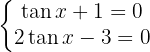
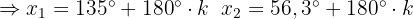
mit 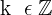
5 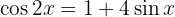
Wir nutzen 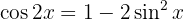 , um die Gleichung in Funkton des Sinus zu schreiben:
, um die Gleichung in Funkton des Sinus zu schreiben:
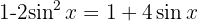
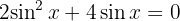
Wir faktorisieren
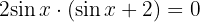
Aus dem 1. Faktor:

mit 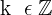
Aus dem 2. Faktor erhalten wir keine Lösung, da 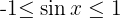
6 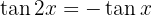
Wir wenden die Identität des Doppelwinkels für den Tangens an: 

Wir vereinfachen den Ausdruck und erhalten

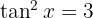
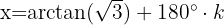
mit 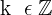
7 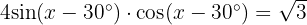
Wir können folgende Identität anwenden: 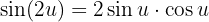



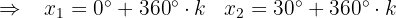
mit 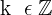
8 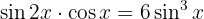
Wir wenden die Identität des Sinus des Doppelwinkels an und erhalten
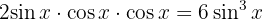
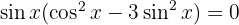
Wir setzen jeden Faktor gleich 0
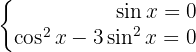
Aus der 1. Gleichung erhalten wir

mit 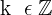
Und aus der 2. Gleichung:
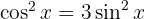

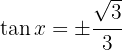

mit 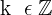
9 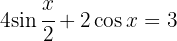
Wir wenden folgende Identität an 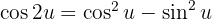
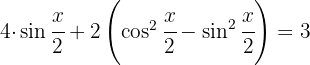
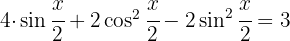
Wir wenden den trigonometrischen Pythagoras des Sinus und Kosinus an
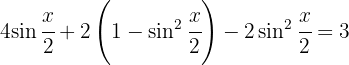
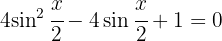
Wir faktorisieren das quadratische Trinom
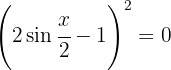



mit 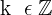
Mit KI zusammenfassen:












