Kapitel
Dies sind Gleichungen, in denen die Unbekannten als Teil der Argumente eines oder mehrerer trigonometrischer Verhältnisse erscheinen. Da diese periodisch sind, gibt es normalerweise unendlich viele Lösungen, wenn die Lösung nicht auf ein bestimmtes Intervall beschränkt ist. Die allgemeine Lösung einer trigonometrischen Gleichung enthält eine ganze Zahl  . Das heißt,
. Das heißt, 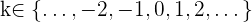 .
.
Um eine trigonometrische Gleichung zu lösen, werden wir die notwendigen Umformungen vornehmen, um mit einer einzelnen trigonometrischen Funktion zu arbeiten, indem wir die grundlegenden trigonometrischen Beziehungen verwenden.

Grundlegende trigonometrische Gleichungen
Ermittle die allgemeine Lösung der folgenden trigonometrischen Gleichungen:
1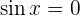
Lösung: Aus der Grafik der Sinusfunktion im Intervall 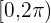 (Abbildung 1) geht hervor, dass die Funktion 0 wird bei den Werten
(Abbildung 1) geht hervor, dass die Funktion 0 wird bei den Werten 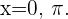 Da die Funktion
Da die Funktion 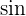 die Periode
die Periode 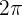 hat, erhalten wir
hat, erhalten wir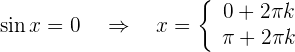 Somit lautet die allgemeine Lösung der Gleichung, vereinfacht geschrieben,
Somit lautet die allgemeine Lösung der Gleichung, vereinfacht geschrieben, 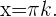
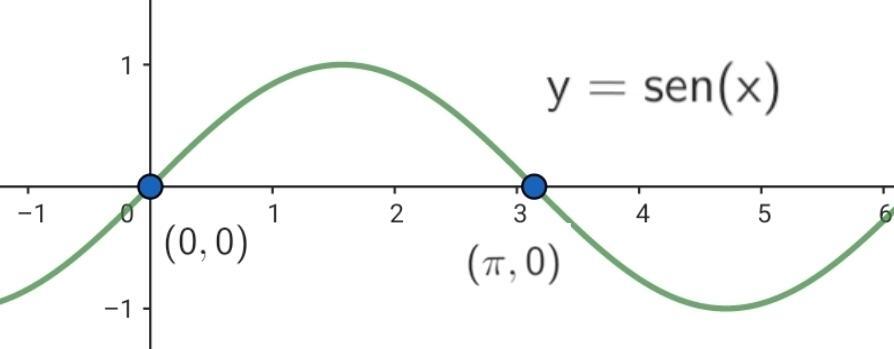
Abbildung 1. Nullstellen der Funktion 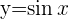 im Intervall
im Intervall 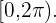
2
Lösung: Aus der Grafik der Kosinusfunktion im Intervall 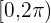 (Abbildung 2) geht hervor, dass die Funktion 0 wird bei den Werten
(Abbildung 2) geht hervor, dass die Funktion 0 wird bei den Werten 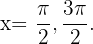 Da die Funktion die Periode
Da die Funktion die Periode  die Periode
die Periode 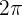 hat, erhalten wir
hat, erhalten wir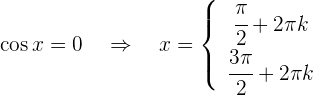 Somit lautet die allgemeine Lösung der Gleichung, vereinfacht geschrieben,
Somit lautet die allgemeine Lösung der Gleichung, vereinfacht geschrieben, 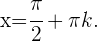
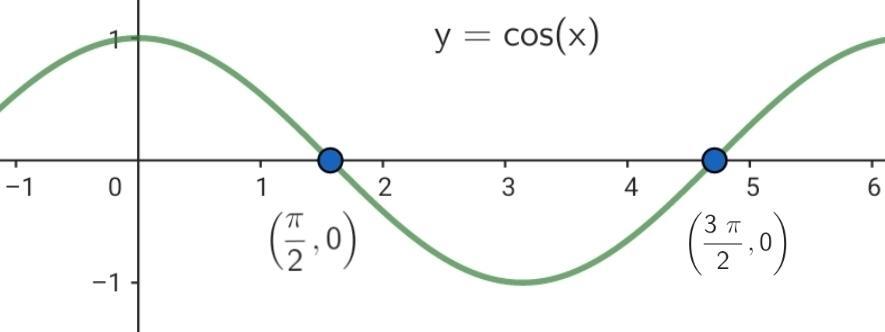
Abbildung 2. Nullstellen der Funktion  im Intervall
im Intervall 
3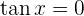
Lösung: Die Tangensfunktion kann auch wie folgt geschrieben werden: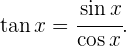 Deshalb gilt
Deshalb gilt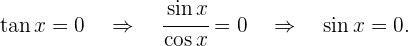 Dies haben wir schon einmal berechnet und die Lösung lautet
Dies haben wir schon einmal berechnet und die Lösung lautet 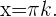 Die Lösung der Gleichung
Die Lösung der Gleichung  ist
ist 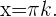
4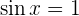
Lösung: Wir wissen, dass für alle 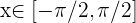 gilt, dass
gilt, dass 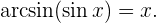 Außerdem gilt für alle
Außerdem gilt für alle  , dass
, dass 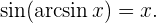 Das heißt, die Funktion
Das heißt, die Funktion 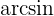 ist die Umkehrfunktion der Funktion
ist die Umkehrfunktion der Funktion 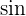 im Intervall
im Intervall 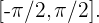 Damit erhalten wir
Damit erhalten wir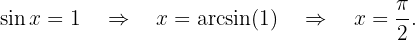 Aus der Periodizität ergibt sich, dass die Lösung der Gleichung wie folgt lautet:
Aus der Periodizität ergibt sich, dass die Lösung der Gleichung wie folgt lautet: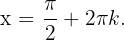
5
Lösung:
Genau wie bei der vorhergehenden Gleichung, ist die Funktion 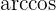 die Umkehrfunktion der Funktion
die Umkehrfunktion der Funktion  im Intervall
im Intervall 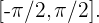 Damit erhalten wir
Damit erhalten wir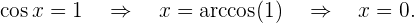
Somit ist die Lösung der Gleichung 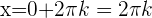 .
.
6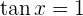
Lösung: Ähnlich wie bei den Funktionen 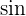 und
und  ist die Funktion
ist die Funktion  die Umkehrfunktion der Funktion
die Umkehrfunktion der Funktion 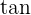 im offenen Intervall
im offenen Intervall  . Somit erhalten wir
. Somit erhalten wir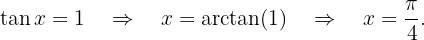 Die Lösung der Gleichung ist
Die Lösung der Gleichung ist 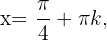 da die Funktion
da die Funktion 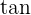 die Periode
die Periode  hat.
hat.
7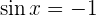
Lösung: Unter Verwendung der Funktion 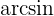 erhalten wir
erhalten wir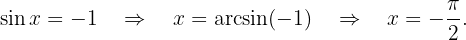
Somit lautet die allgemeine Gleichung 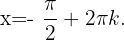
8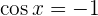
Lösung: Unter Verwedndung der Funktion 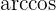 erhalten wir
erhalten wir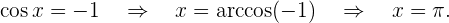
Somit lautet die allgemeine Gleichung 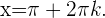
9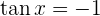
Lösung: Unter Verwedndung der Funktion 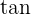 erhalten wir
erhalten wir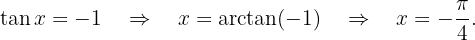
Somit lautet die allgemeine Gleichung 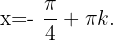
Hinweis: Die Lösungen trigonometrischer Gleichungen werden häufiger in Bogenmaß als in Grad angegeben, können aber mit der folgenden Formel in Grad umgerechnet werden: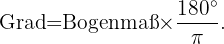 Die Lösung der ersten Gleichung in Grad lautet zum Beispiel
Die Lösung der ersten Gleichung in Grad lautet zum Beispiel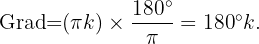
Das heißt: 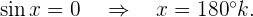
Beispiele für das Lösen trigonometrischer Gleichungen
Im Folgenden werden wir verschiedene trigonometrische Gleichungen mit höherem Schwierigkeitsgrad und deren Lösung betrachten.
1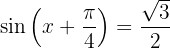
Lösung: Die gängigsten Winkel der grundlegenden trigonometrischen Funktionen besagen, dass im Intervall  ,
,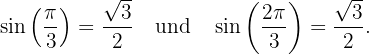
Und somit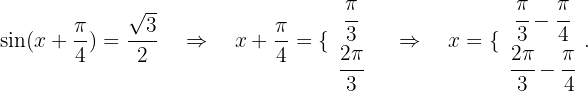
Das heißt 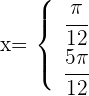
Somit ist die allgemeine Lösung der trigonometrischen Gleichung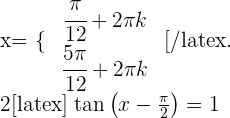
Lösung: Die gängigsten Winkel der grundlegenden trigonometrischen Funktionen besagen, dass 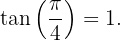
Es gilt also 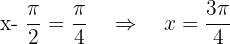
Somit lautet die Lösung 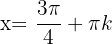 ,
,
da 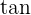 die Periode
die Periode  hat.
hat.
3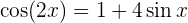
Lösung: Unter Verwendung der trigonometrischen Beziehungen 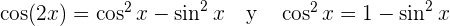 erhalten wir
erhalten wir
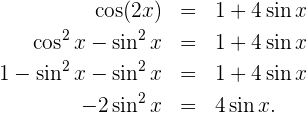
Und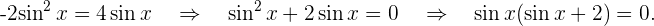
Somit ist 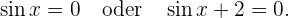
Die erste Gleichung wurde bereits oben gelöst. Die Lösung lautet 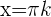 . Die Gleichung
. Die Gleichung 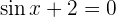 hat keine Lösung, da
hat keine Lösung, da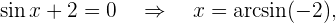
jedoch ist  nicht in der Definitionsmenge der Funktion
nicht in der Definitionsmenge der Funktion 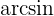 enthalten und es existiert somit auch keine Lösung. Schließlich lautet die Lösung der Gleichung
enthalten und es existiert somit auch keine Lösung. Schließlich lautet die Lösung der Gleichung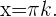
4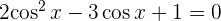
Lösung: Wir faktorisieren und erhalten
Somit gilt:
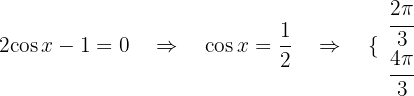
und 
im Intervall 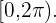
Schließlich ist die Lösung 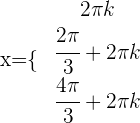
5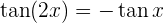
Lösung: Um diese Aufgabe zu lösen, wenden wir Folgendes an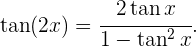
Somit erhalten wir
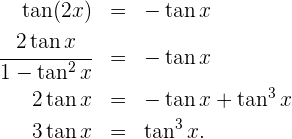
Und wenn: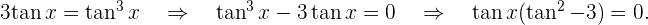
Deshalb gilt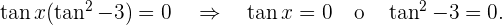
Die erste Gleichung haben wir bereits gelöst. Ihre Lösung ist  Nun lösen wir die zweite Gleichung
Nun lösen wir die zweite Gleichung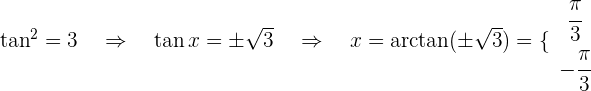

Schließlich lautet die allgemeine Lösung der Gleichung
6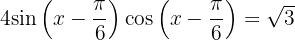
Lösung:
Unter Verwendung von 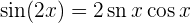
erhalten wir
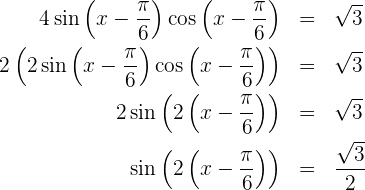
Nach der gleichen Argumentation wie in der ersten Übung ergibt sich dann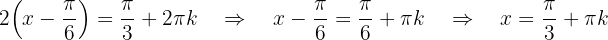
und 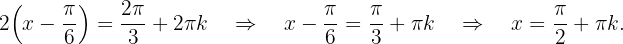
Die Lösung der Gleichung lautet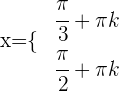
Mit KI zusammenfassen:












