Kapitel

Grundlegende trigonometrische Identitäten
1 Zusammenhang zwischen Sinus und Kosinus
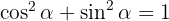
2 Zusammenhang zwischen Sekans und Tangens
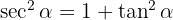
3 Zusammenhang zwischen Kosekans und Kotangens

4 Reziproke trigonometrische Funktionen
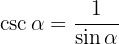
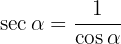

Beispiele mit Aufgaben zu trigonometrischen Identitäten
Gegeben ist 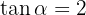 und
und 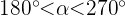 . Berechne die verbleibenden trigonometrischen Funktionen des Winkels
. Berechne die verbleibenden trigonometrischen Funktionen des Winkels  .
.
Wir ermitteln die verbleibenden trigonometrischen Funktionen in Abhängigkeit von diesem Winkel.Wir beginnen mit  , da wir ihn direkt mit
, da wir ihn direkt mit 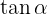 bestimmen können
bestimmen können
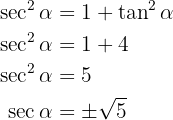
Wir stellen jedoch fest, dass für den Quadranten, in dem  definiert ist,
definiert ist, 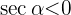 gilt. Somit ist
gilt. Somit ist 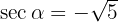 .
.
Nun können wir 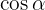 bestimmen
bestimmen
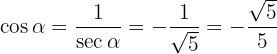
Wir erhalten 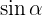 und davon ausgehend
und davon ausgehend 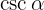 . Und genau wie bei
. Und genau wie bei 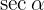 , muss der Sinus für den Quadranten, in dem
, muss der Sinus für den Quadranten, in dem  definiert ist, negativ sein. Also
definiert ist, negativ sein. Also
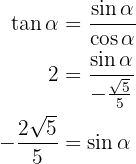
So haben wir bereits 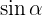 ermittelt und stellen fest, dass
ermittelt und stellen fest, dass
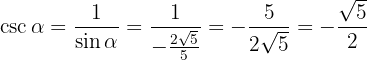
Schließlich bestimmen wir 
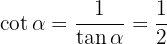
Gegeben ist 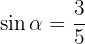 und
und 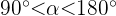 . Berechne die verbleibenden trigonometrischen Funktionen des Winkels
. Berechne die verbleibenden trigonometrischen Funktionen des Winkels  .
.
Wir ermitteln die verbleibenden trigonometrischen Funktionen in Abhängigkeit von diesem Winkel. Wir beginnen mit 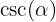 , da wir direkt berechnen können
, da wir direkt berechnen können

Nun können wir 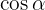 bestimmen. Für das Intervall, in dem
bestimmen. Für das Intervall, in dem  definiert ist, ist der Kosinus negativ. Also
definiert ist, ist der Kosinus negativ. Also
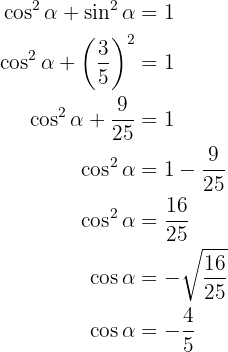
Da wir bereits den Kosinus haben, können wir 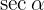 direkt berechnen
direkt berechnen

Nun müssen wir nur noch Tangens und Kotangens berechnen; hierzu nutzen wir den Sinus und den Kosinus

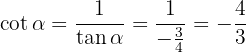
Trigonometrische Funktionen – Summe und Differenz von Winkeln
1. 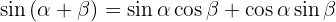
2. 
3. 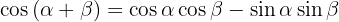
4. 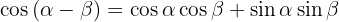
5. 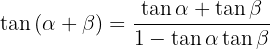
6. 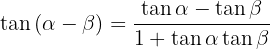
Beispielaufgaben zu Summe und Differenz von Winkeln
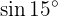
Um diese Aufgabe zu lösen, schreiben wir unseren Winkel als Summe von zwei bestimmten Winkeln, um die Formeln der trigonometrischen Funktionen zu verwenden, die bei der Addition und Subtraktion von Winkeln angewendet werden
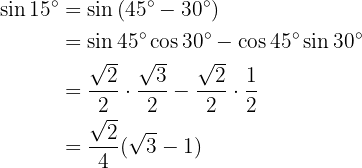

Um diese Aufgabe zu lösen, schreiben wir unseren Winkel als Summe von zwei bestimmten Winkeln, um die Formeln der trigonometrischen Funktionen zu verwenden, die bei der Addition und Subtraktion von Winkeln angewendet werden
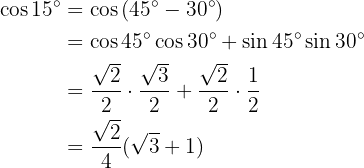
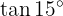
Um diese Aufgabe zu lösen, schreiben wir unseren Winkel als Summe von zwei bestimmten Winkeln, um die Formeln der trigonometrischen Funktionen zu verwenden, die bei der Addition und Subtraktion von Winkeln angewendet werden
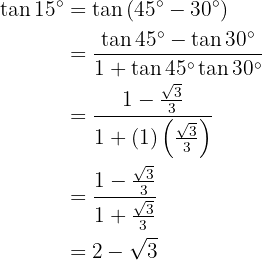
Doppelwinkelfunktionen
1. 
2. 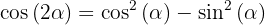
3. 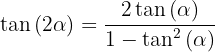
Aufgaben zum Doppelwinkel
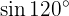
Um diese Aufgabe zu lösen, ermitteln wir zunächst die Hälfte des gegebenen Winkels und nutzen dann die Formel für die entsprechende Doppelwinkelfunktion:
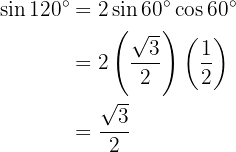
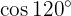
Um diese Aufgabe zu lösen, ermitteln wir zunächst die Hälfte des gegebenen Winkels und nutzen dann die Formel für die entsprechende Doppelwinkelfunktion:
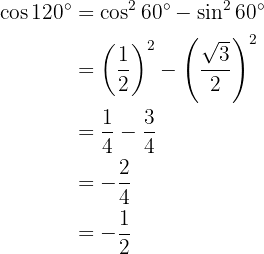
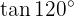
Um diese Aufgabe zu lösen, ermitteln wir zunächst die Hälfte des gegebenen Winkels und nutzen dann die Formel für die entsprechende Doppelwinkelfunktion:
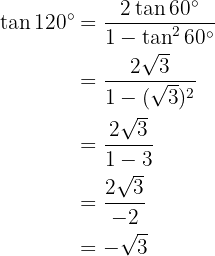
Halbwinkelfunktionen
1. 
2. 
3. 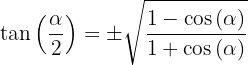
Aufgaben zum Halbwinkel
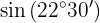
Um diese Aufgabe zu lösen, ermitteln wir zunächst das Doppelte des gegebenen Winkels und wenden dann die Formel an, die der gegebenen trigonometrischen Funktion entspricht. Für den Quadranten, in dem der Winkel liegt, ist der Wert des Sinus positiv.
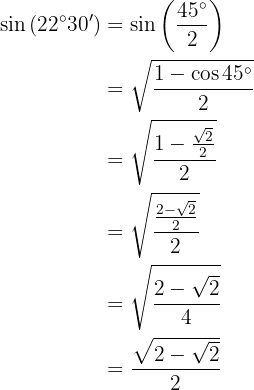

Um diese Aufgabe zu lösen, ermitteln wir zunächst das Doppelte des gegebenen Winkels und wenden dann die Formel an, die der gegebenen trigonometrischen Funktion entspricht. Für den Quadranten, in dem der Winkel liegt, ist der Wert des Kosinus positiv.
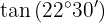
Um diese Aufgabe zu lösen, ermitteln wir zunächst das Doppelte des gegebenen Winkels und wenden dann die Formel an, die der gegebenen trigonometrischen Funktion entspricht. Für den Quadranten, in dem der Winkel liegt, ist der Wert des Tangens positiv.
Umwandlung von Rechenoperationen
Umwandlung von Summen in Produkte
1. 
2. 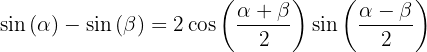
3. 
4. 
Beispielaufgaben für die Umwandlung von Summe in Produkt
In den nächsten Aufgaben schreiben wir nicht den Wert der Summe oder der Differenz der trigonometrischen Funktionen, sondern wandeln ihn einfach in ein Produkt anderer trigonometrischer Funktionen um, je nach der zu verwendenden Formel.
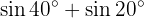
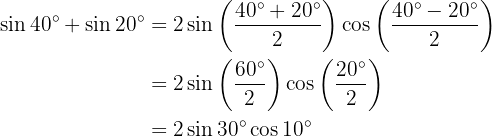
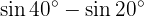
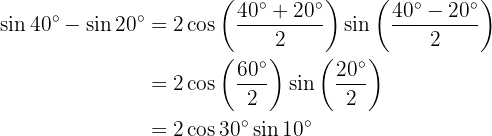
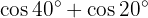
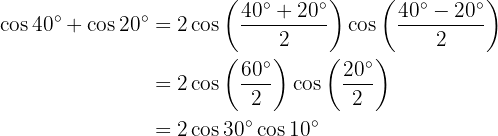
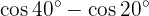
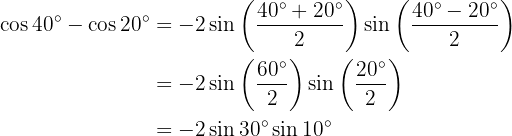
Umwandlung von Produkten in Summen
1. 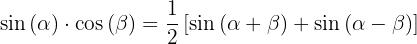
2. 
3. 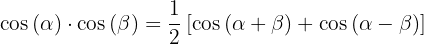
4. 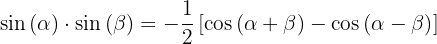
Beispielaufgabe für die Umandlung von Produkt in Summe
In den nächsten Aufgaben schreiben wir nicht den Wert der Multiplikation der trigonometrischen Funktionen, sondern wandeln ihn einfach in eine Summe oder Differenz anderer trigonometrischer Funktionen um, je nach der zu verwendenden Formel.
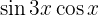

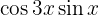
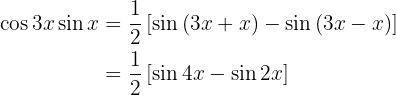
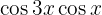
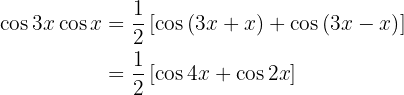

Mit KI zusammenfassen:













