Mit der Methode der partiellen Integration können wir das Integral eines Produkts zweier Funktionen berechnen. Wir wenden folgende Formel an:
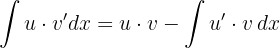
Logarithmusfunktionen, Arkusfunktionen und Polynomfunktionen werden mit  angegeben.
angegeben.
Exponentialfunktionen sowie Sinus- und Kosinusfunktionen werden mit 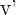 angegeben
angegeben
.

Fall 1
Im ersten Fall wenden wir die Formel direkt an, wobei wir  als
als  nehmen.
nehmen.
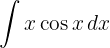
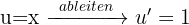
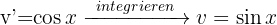
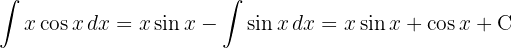
Fall 2
Wenn wir durch partielle Integration ein Polynom vom Grad  erhalten, nehmen wir es als
erhalten, nehmen wir es als  und wiederholen den Vorgang
und wiederholen den Vorgang  Mal.
Mal.
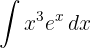
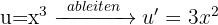
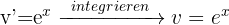
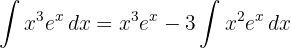
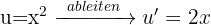
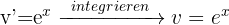
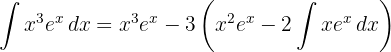
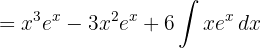
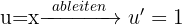
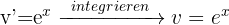
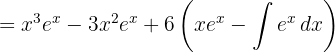
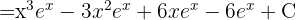
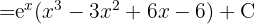
Fall 3
Wenn wir ein Integral mit nur einem Logarithmus oder einem "Arkus" haben, integrieren wir partiell, indem wir nehmen: 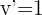 .
.

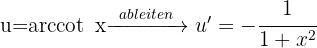
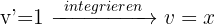
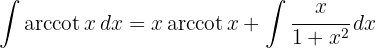
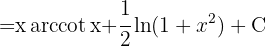
Fall 4
Wenn bei der partiellen Integration das zu berechnende Integral im zweiten Glied erscheint, wird es als Gleichung gelöst.

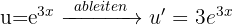

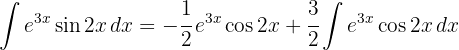
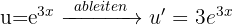
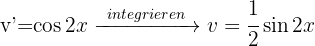

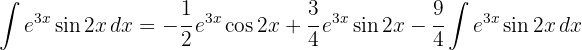
Wir bringen das Integral von der rechten auf die linke Seite der Gleichung.

Wir addieren die Integrale und multiplizieren beide Seiten mit 4/13.

Wir klammern den gemeinsamen Faktor  aus.
aus.
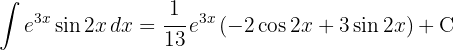
Mit KI zusammenfassen:












