
Trigonometrische Funktionen von verschiedenen Winkeln
Komplementärwinkel
Zwei Winkel 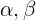 sind komplementär, wenn ihre Summe gleich
sind komplementär, wenn ihre Summe gleich  ist. Dies entspricht einem Bogenmaß von
ist. Dies entspricht einem Bogenmaß von 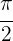 . Für zwei komplementäre Winkel gilt:
. Für zwei komplementäre Winkel gilt:

Wir drücken die trigonometrischen Funktionen Sinus, Kosinus und Tangens eines Komplementärwinkels in Form ihres Komplements aus:
1 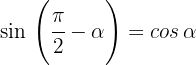
2 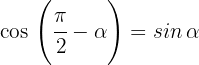
3 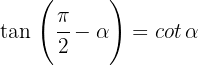
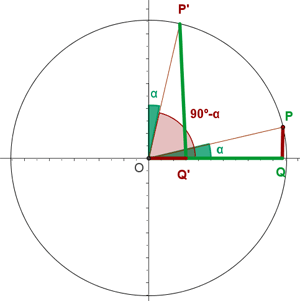
Beispiel: Berechne
1 
Das Komplement des Winkels  ist
ist  . Somit
. Somit
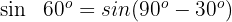
Wir verwenden die Formel für den Sinus des Komplements eines Winkels
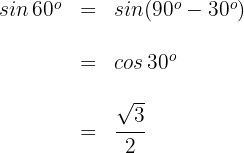
2 
Das Komplement des Winkels  ist
ist  . Somit
. Somit

Wir verwenden die Formel für den Kosinus des Komplements eines Winkels
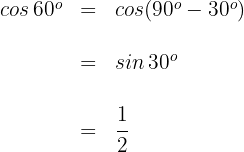
3 
Das Komplement des Winkels  ist
ist  . Somit
. Somit
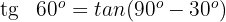
Wir verwenden die Formel für den Tangens des Komplements eines Winkels
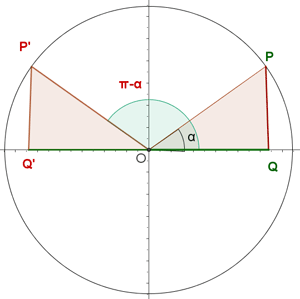
Supplementwinkel
Zwei Winkel 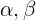 sind supplementär, wenn ihre Summe
sind supplementär, wenn ihre Summe  ist. Dies entspricht einem Bogenmaß von
ist. Dies entspricht einem Bogenmaß von  . Für zwei Supplementwinkel gilt:
. Für zwei Supplementwinkel gilt:

Wir drücken die trigonometrischen Funktionen Sinus, Kosinus und Tangens eines Supplementwinkels in Form seines Supplements aus:
1 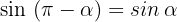
2 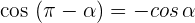
3 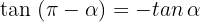
Beispiel: Berechne
1 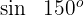
Das Supplement des Winkels 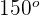 ist
ist  . Somit
. Somit
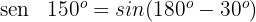
Wir wenden die Formel für den Sinus des Supplements eines Winkels an
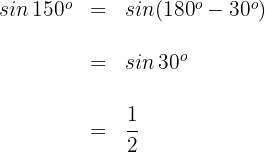
2 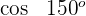
Das Supplement des Winkels 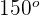 ist
ist  . Somit
. Somit
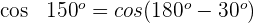
Wir verwenden die Formel für den Kosinus des Supplements eines Winkels
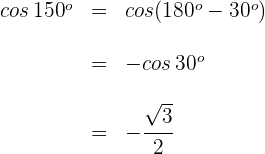
3 
Das Supplement des Winkels 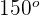 ist
ist  . Somit
. Somit
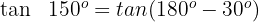
Wir verwenden die Formel für den Tangens des Supplements eines Winkels
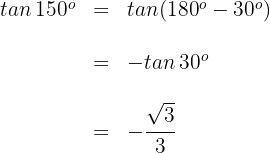
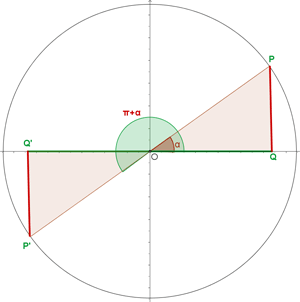
Winkel, die von  abweichen
abweichen
Wir drücken die trigonometrischen Funktionen Sinus, Kosinus und Tangens für diese Art von Winkeln aus:
1 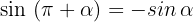
2 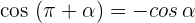
3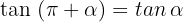
Beispiel: Berechne
1 
Dieser Winkel wird mit 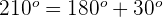 ausgedrückt. Somit
ausgedrückt. Somit
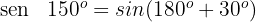
Wir wenden die 1. Formel an und erhalten
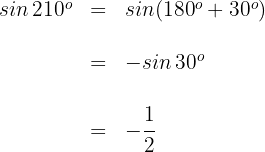
2 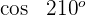
Dieser Winkel wird mit 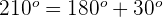 ausgedrückt. Somit
ausgedrückt. Somit

Wir wenden die 2. Formel an und erhalten

3 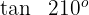
Dieser Winkel wird mit 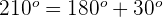 ausgedrückt. Somit
ausgedrückt. Somit
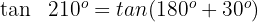
Wir wenden die 3. Formel an und erhalten
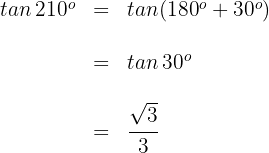
Scheitelwinkel
Wir drücken die trigonometrischen Funktionen Sinus, Kosinus und Tangens für diese Art von Winkeln aus:
1 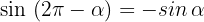
2 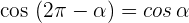
3 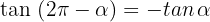
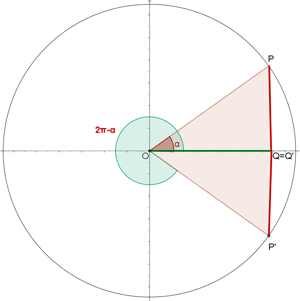
Beispiel: Berechne
1 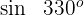
Dieser Winkel wird als  ausgedrückt. Somit
ausgedrückt. Somit
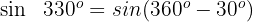
Wir wenden die 1. Formel an und erhalten
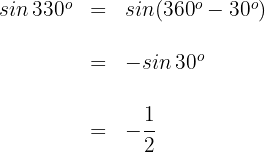
2 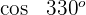
Dieser Winkel wird als  ausgedrückt. Somit
ausgedrückt. Somit

Wir wenden die 2. Formel an und erhalten
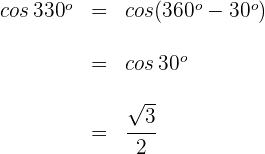
3 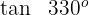
Dieser Winkel wird als  ausgedrückt. Somit
ausgedrückt. Somit
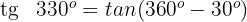
Wir wenden die 3. Formel an und erhalten
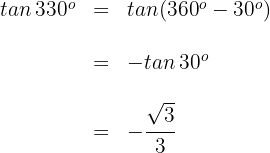
Negative Winkel
Wir drücken die trigonometrischen Funktionen Sinus, Kosinus und Tangens für diese Art von Winkeln aus:
1 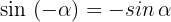
2 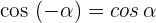
3 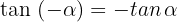
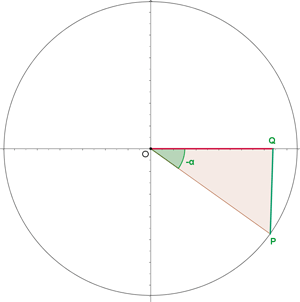
Beispiel: Berechne
1 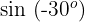
Wir wenden die 1. Formel an und erhalten
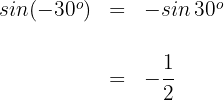
2 
Wir wenden die 2. Formel an und erhalten

3 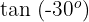
Wir wenden die 3. Formel an und erhalten
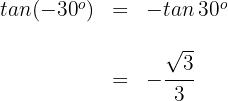
Winkel größer als 
Wir drücken die trigonometrischen Funktionen Sinus, Kosinus und Tangens für diese Art von Winkeln aus:
1 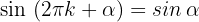
2 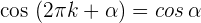
3 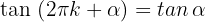
Beispiel: Berechne
1 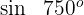
Dieser Winkel wird als  ausgedrückt. Somit
ausgedrückt. Somit
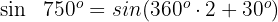
Wir wenden die 1. Formel an und erhalten
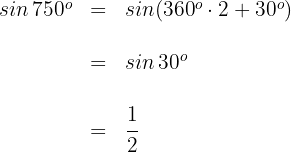
2 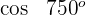
Dieser Winkel wird als  ausgedrückt. Somit
ausgedrückt. Somit
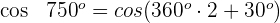
Wir wenden die 2. Formel an und erhalten
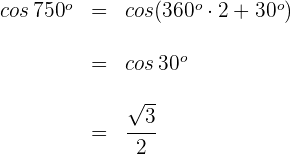
3 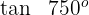
Dieser Winkel wird als  ausgedrückt. Somit
ausgedrückt. Somit
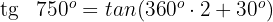
Wir wenden die 3. Formel an und erhalten
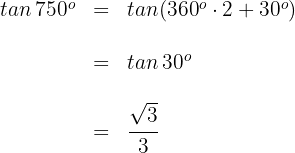
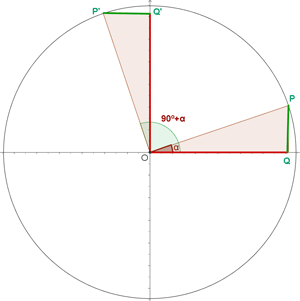
Winkel, die von  abweichen
abweichen
Wir drücken die trigonometrischen Funktionen Sinus, Kosinus und Tangens für diese Art von Winkeln aus:
1 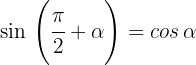
2 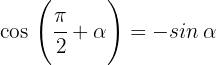
3 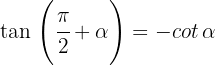
Beispiel: Berechne
1 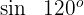
Dieser Winkel wird als 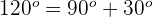 ausgedrückt. Somit
ausgedrückt. Somit
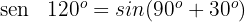
Wir wenden die 1. Formel an und erhalten
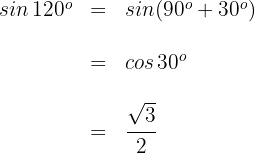
2 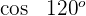
Dieser Winkel wird als 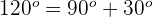 ausgedrückt. Somit
ausgedrückt. Somit
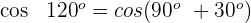
Wir wenden die 2. Formel an und erhalten
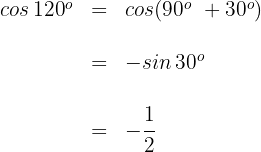
3 
Dieser Winkel wird als 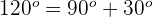 ausgedrückt. Somit
ausgedrückt. Somit
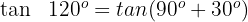
Wir wenden die 3. Formel an und erhalten
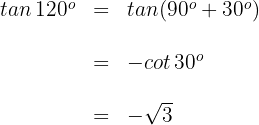
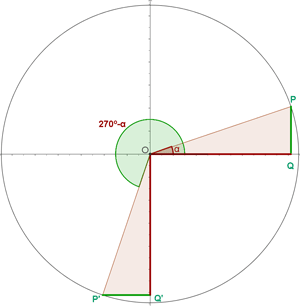
Winkel, die in der Summe 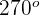 ergeben
ergeben
Wir drücken die trigonometrischen Funktionen Sinus, Kosinus und Tangens für diese Art von Winkeln aus:
1 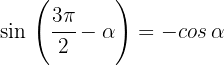
2 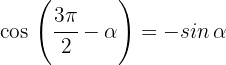
3 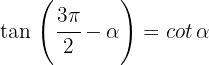
Beispiel: Berechne
1 
Dieser Winkel wird als  ausgedrückt. Somit
ausgedrückt. Somit
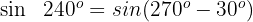
Wir wenden die 1. Formel an und erhalten
2 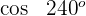
Dieser Winkel wird als  ausgedrückt. Somit
ausgedrückt. Somit
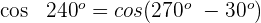
Wir wenden die 2. Formel an und erhalten
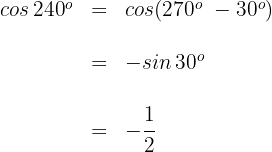
3 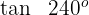
Dieser Winkel wird als  ausgedrückt. Somit
ausgedrückt. Somit
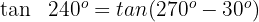
Wir wenden die 3. Formel an und erhalten
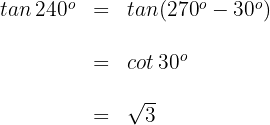
Winkel, die von 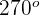 abweichen
abweichen
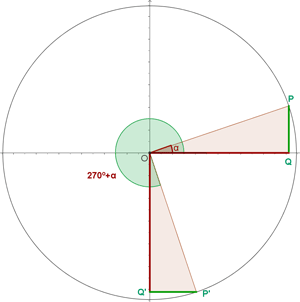
Wir drücken die trigonometrischen Funktionen Sinus, Kosinus und Tangens für diese Art von Winkeln aus:
1 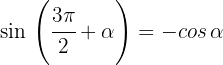
2 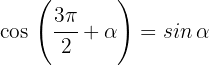
3 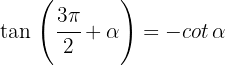
Beispiel: Berechne
1 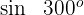
Dieser Winkel wird als 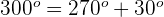 ausgedrückt. Somit
ausgedrückt. Somit
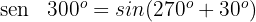
Wir wenden die 1. Formel an und erhalten
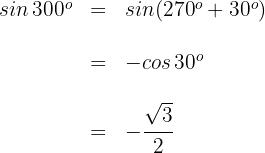
2 
Dieser Winkel wird als 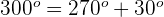 ausgedrückt. Somit
ausgedrückt. Somit
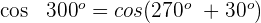
Wir wenden die 2. Formel an und erhalten
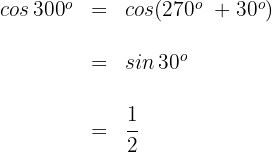
3 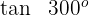
Dieser Winkel wird als 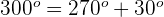 ausgedrückt. Somit
ausgedrückt. Somit
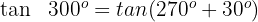
Wir wenden die 3. Formel an und erhalten
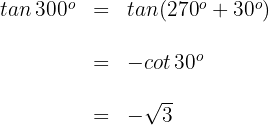
Aufgaben
Führe folgende Berechnungen durch:
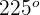
1 Dieser Winkel wird als 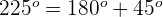 ausgedrückt. Wir wenden also die Formel für Winkel an, die von
ausgedrückt. Wir wenden also die Formel für Winkel an, die von  abweichen.
abweichen.
2 Wir berechnen 
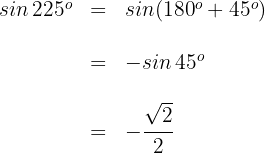
3 Wir berechnen 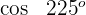
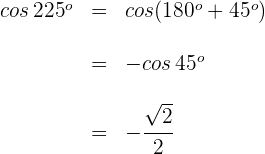
4 Wir berechnen 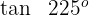
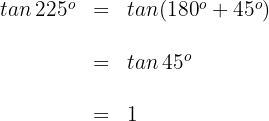
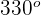
1 Dieser Winkel wird als  . Wir wenden also die Formel für Scheitelwinkel an
. Wir wenden also die Formel für Scheitelwinkel an
2 Wir berechnen 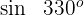
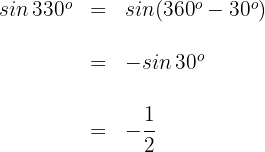
3 Wir berechnen 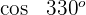
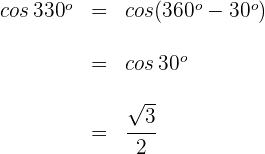
4 Wir berechnen 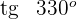
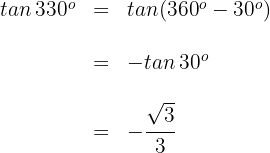

1 Dieser Winkel wird als 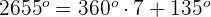 ausgedrückt. Wir wenden also die Formel für Winkel an, die größer als
ausgedrückt. Wir wenden also die Formel für Winkel an, die größer als  sind
sind
2 Wir berechnen 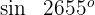
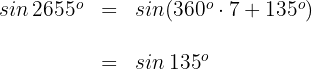
Wir wenden die Formel für Supplementwinkel an
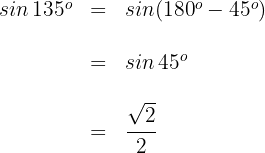
3 Wir berechnen 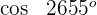
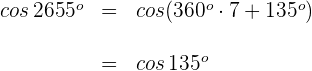
Wir wenden die Formel für Supplementwinkel an
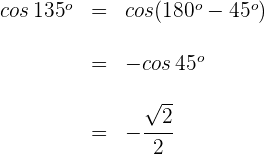
4 Wir berechnen 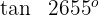
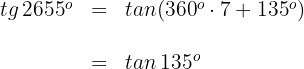
Wir wenden die Formel für Supplementwinkel an
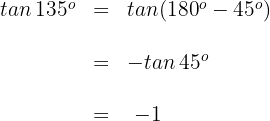

1 Dieser Winkel wird als 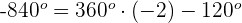 ausgedrückt. Wir wenden also die Formel für Winkel an, die größer als
ausgedrückt. Wir wenden also die Formel für Winkel an, die größer als  sind
sind
2 Wir berechnen 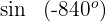
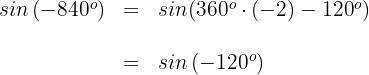
Wir wenden die Formel für negative Winkel und die für Supplementwinkel an
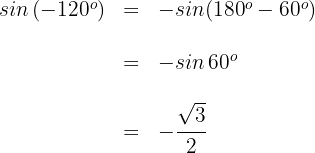
3 Wir berechnen 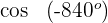
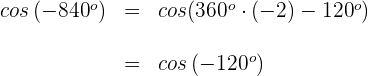
Wir wenden die Formel für negative Winkel und die für Supplementwinkel an
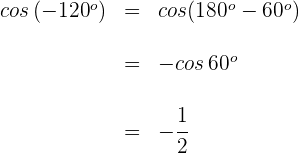
4 Wir berechnen 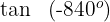
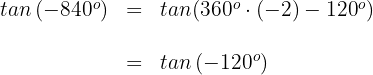
Wir wenden die Formel für negative Winkel und die für Supplementwinkel an
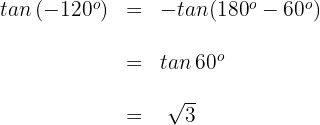
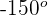
1 Wir wenden die Formel für negative Winkel und danach die Formel für Supplementwinkel an
2 Wir berechnen 
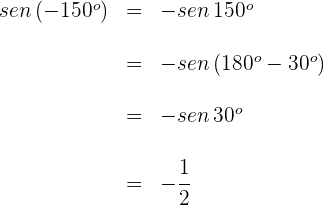
3 Wir berechnen 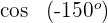
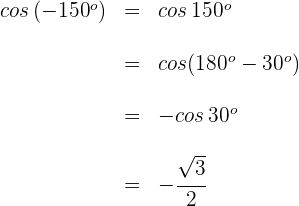
4 Wir berechnen 
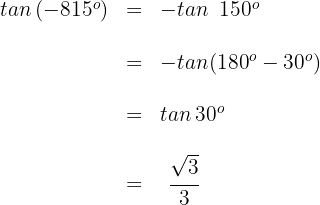
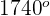
1 Dieser Winkel wird als 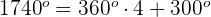 ausgedrückt. Wir wenden also die Formel für Winkel an, die größer als
ausgedrückt. Wir wenden also die Formel für Winkel an, die größer als  sind
sind
2 Wir berechnen 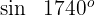
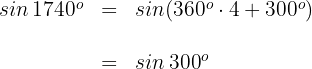
Wir wenden die Formel für Winkel an, die von 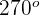 abweichen
abweichen
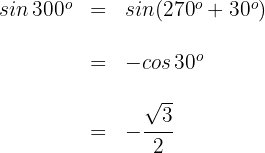
3 Wir berechnen 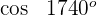

Wir wenden die Formel für Winkel an, die von 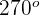 abweichen
abweichen
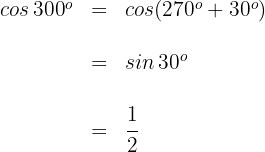
4 Wir berechnen 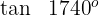
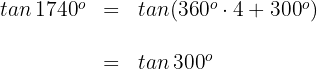
Wir wenden die Formel für Winkel an, die von 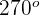 abweichen
abweichen
Mit KI zusammenfassen:












